高三数学试题1
参考公式:
![]()
![]()
![]()
![]()
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四项中只有一项是符
合题目要求的.
1.设函数![]() 的定义域是
的定义域是![]() ,则
,则![]() 的定义域是 ( )
的定义域是 ( )
A.[0,2] B.[-1,1] C.[-2,0] D.[1,3]
2.复数![]() 的值是 ( )
的值是 ( )
A.![]() B.
B.![]() C.-1 D.1
C.-1 D.1
|
|
A B C D
4.(理)在同一极坐标系中,两曲线![]() )的位置关
)的位置关
系是 ( )
A.相切 B.相交 C.相离 D.其它
(文)如果![]() 轴相切于原点,那么 ( )
轴相切于原点,那么 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.若一个三棱锥中,有一条棱长为![]() ,其余棱长均为1,则体积V(
,其余棱长均为1,则体积V(![]() )取得最大值时的
)取得最大值时的![]()
的值是 ( )
A.1 B.![]() C.
C.![]() D.
D.![]()
6.正项等比数列{![]() }的首项
}的首项![]() ,其前11项的几何平均数为25,若前11项中抽出一
,其前11项的几何平均数为25,若前11项中抽出一
项后的几何平均数仍为25,则抽去的一项的项数为 ( )
A.6 B.7 C.9 D.11
7.过双曲线![]() 的右焦点作直线
的右焦点作直线![]() 交双曲线于A、B两点,AB=4,则这
交双曲线于A、B两点,AB=4,则这
样的直线有 ( )
A.4条 B.3条 C.2条 D.1条
8.(理)若![]() ,则
,则![]() 的取值范围为 ( )
的取值范围为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)若函数![]() 的最小值为
的最小值为![]() ,则其最小正周期是( )
,则其最小正周期是( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
9.在四棱台的6个面中选取3个面,其中有两个面不相邻的选法共有 ( )
A.20 B.16 C.12 D.8
10.已知长方形的四个顶点A(1,0),B(3,0),C(3,1),D(1,1),一小球从A点出
发,沿与AB夹角为锐角![]() 的方向射到BC上的点P1后,依次反射到CD,DA和AB上
的方向射到BC上的点P1后,依次反射到CD,DA和AB上
的点P2,P3和P4(入射角等于反射角)。设P4的坐标为(![]() ,0). 若
,0). 若![]() ,则
,则![]()
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.一个球面的内接四面体的所有棱长为1,此球的表面积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.在数列{![]() }中,有
}中,有![]() 并有
并有![]() 存在,则
存在,则![]() 的值为( )
的值为( )
A.0 B.![]() C.2 D.不存在
C.2 D.不存在
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.二项项![]() 的展开式中
的展开式中![]() 的系数是
(用数字表示).
的系数是
(用数字表示).
14.若![]() ,则不等式
,则不等式![]() 的解为
.
的解为
.
15.给四棱锥V—ABCD的五个面涂颜色,要求相邻的两个面不得使用同一种颜色,现有4
种颜色供选择,则不同的涂色方法共有 种(以数字作答).
16.双曲线![]() 上的点P到一条准线的距离为2,则点P到两焦点的距离
上的点P到一条准线的距离为2,则点P到两焦点的距离
为 .
三、解证题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17(本题满分12分)
已知函数![]()
(1)求![]() 的最大值与最小值;
的最大值与最小值;
(2)若![]() 的值.
的值.
18.(本题满分12分)
为了保卫西安的母亲河——渭河,某厂投资50万元建成一个处理系统,把污染环境的废料变成有用的生产原料,如果这个系统每月用2万元的成本进行生产,那么生产收入(单位:万元)与生产时间![]() (单位:月)的关系为
(单位:月)的关系为![]() 问:
问:
(1)至少需要经过几个月,生产收入与总投入能基本平衡?
(2)经过几个月可获得最大利润?
19.(本题满分12分)
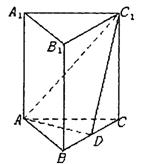
如图,正三棱柱各棱长都相等,D是BC上一点,AD⊥C1D
(1)求证:截面ADC1⊥侧面BCC1B1;
|
20.(本题满分12分)
若![]() ,求使关于
,求使关于![]() 的方程
的方程![]() 有解的正数
有解的正数![]() 的取值范围.
的取值范围.
21.(本题满分12分)
函数![]() ,当点P(
,当点P(![]() )是函数
)是函数![]() 图象上的点时,Q(
图象上的点时,Q(![]() 是函数
是函数![]() 图象上的点.
图象上的点.
(Ⅰ)写出函数![]() 的解析式;
的解析式;
(Ⅱ)(理)当![]() 时,恒有
时,恒有![]() ,试确定
,试确定![]() 的取值范围.
的取值范围.
(文)当![]() 时,确定函数
时,确定函数![]() 的单调性.
的单调性.
22.(本题满分14分)
椭圆E的中心在原点O,焦点在![]() 轴上,其离心率
轴上,其离心率![]() ,过点C(-1,0)的直线
,过点C(-1,0)的直线
![]() 与椭圆E相交于A、B两点,且C分有向线段
与椭圆E相交于A、B两点,且C分有向线段![]() 的比为2.
的比为2.
(Ⅰ)用直线![]() 的斜率
的斜率![]() 表示△OAB的面积;
表示△OAB的面积;
(Ⅱ)(理科作,文科不做)当△OAB的面积最大时,求椭圆E的方程.
高三数学参考答案及评分标准
一、DCCA DABB CDAB
二、13.-56
14.![]() 15.
15.![]() 16.
16.![]()
17.解:(1)![]()
![]() ……2分
……2分
![]() ……4分
……4分
![]() ……6分
……6分
(2)由![]() ……8分
……8分
![]() ……10分
……10分
即![]() ……12分
……12分
18.解:设要过![]() 个月生产收入与总投入才能基本平衡,即
个月生产收入与总投入才能基本平衡,即
![]() ]
]
![]()
至少需要5个月,生产收入与总投入基本平衡.……8分
令利润为![]() 则
则![]() ……10分
……10分
![]()
经过50个月,可获得最大利润50万元. ……12分.
19.(1)证明:∵三棱柱为正三棱柱,∴CC1⊥面ABC, ∵AD⊥C1D ∴AD⊥CD
∴AD⊥BCC1B1 又AD![]() 面ADC1,∴面ADC1⊥面BCC1B1……4分
面ADC1,∴面ADC1⊥面BCC1B1……4分
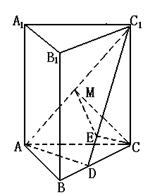
(2)解:由(1)知,D为BC的中点,设棱长均为![]() ,作CE⊥C1D,垂足为E,
,作CE⊥C1D,垂足为E,
作EM⊥AC1,垂足为M,连结CM ……6分 ∵AD⊥面BC1 ∴AD⊥CE
∴CE⊥面ADC1,由三垂线定理知CM⊥AC1,
所以∠CME为二面角C—AC1—D的平面角
在Rt△CEM中,C1D=![]() ,∴CE·
,∴CE·![]() ,∴CE=
,∴CE=![]() ……10分
……10分
|
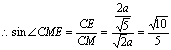
![]()
∴二面角C—AC1—D为![]() ……12分
……12分
20.解:![]() ,故方程两边同时平方得:
,故方程两边同时平方得:
![]() ……3分
……3分
![]() 两边同除以
两边同除以![]()
![]() ……6分
……6分 ![]()
![]() ……9分
……9分
即 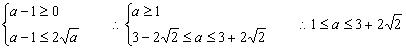 ……12分
……12分
另解:由题![]()
![]() ……5分
……5分
![]() 随
随![]() 增大而增大 ∴随
增大而增大 ∴随![]() 的增大,
的增大,![]() 增大,
增大,
而![]() 减小 于是,
减小 于是,![]() 时,是
时,是![]() 的增函数…9分
的增函数…9分
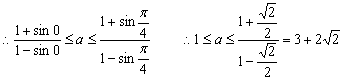 ……12分
……12分
21.解:(Ⅰ)设P(![]() 是
是![]() 图象上点,Q(
图象上点,Q(![]()
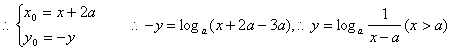 …………5分
…………5分
(2)(理)![]()
![]() 上有意义
上有意义 ![]() …………6分
…………6分
![]() 恒成立
恒成立
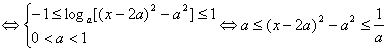 ………………8分
………………8分
对![]()
其对称轴![]()
![]()
![]()
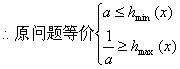 …………10分
…………10分
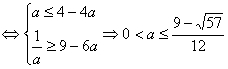 ………………12分
………………12分
![]()
![]() 上有意义
上有意义 ![]()
![]() …………8分
…………8分
在![]() ,
,
则t是x的减函数,![]() 的减函数
的减函数
又由复合函数的单调性知,![]()
当![]() 时是x的增函数.…………………………12分
时是x的增函数.…………………………12分
22.解:(1)设椭圆E的方程为![]()
![]() ,故椭圆方程
,故椭圆方程![]() ………………1分
………………1分
设![]() 、
、![]() ,由于点C(-1,0)分有向线段
,由于点C(-1,0)分有向线段![]() 的比为2,
的比为2,
![]()
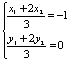 即
即![]() ……………………3分
……………………3分
由题:![]()
由![]() 消去y整理并化简得
消去y整理并化简得![]()
由直线![]() 与椭圆E相交于
与椭圆E相交于![]() 两点
两点
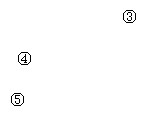
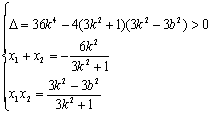 ……………………5分
……………………5分
而![]() ⑥
⑥
由①,④得:![]()
![]()
![]()
代入⑥得:![]() ……8分
……8分
(2)因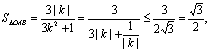 当且仅当
当且仅当![]() 取得最大值
取得最大值
此时![]() …10分
…10分 ![]()
![]() 代入⑤得
代入⑤得![]() ∴椭圆方程
∴椭圆方程![]() ……14分
……14分