高考数学仿真试题(三)答案

高考数学仿真试题(三)答案

一、选择题

1.D　2.B　3.C  4.A　5.D　6.C  7.D　8.B　9.B  10.A　11.A　12.B

二、填空题

13.4　14.24789　　15.4　　16.

三、解答题

17.解：（1）g(x)=x-2+

(2)当a＞1时不等式的解集为{x＜x＜6}

当0＜a＜1时不等式的解集为{x4＜x＜或x＞6}

18.解：a=(2cos²,2sincos)

=2cos (cos,sin)

∴θ₁=,

b=(2sin²,2sincos)

=2sin (sin,cos)

∴θ₂=－,又θ₁－θ₂=－⁺== －

∴sin=sin(－)=－

19.解：（1）设{a_n}的首项为a,公差为d,

∴

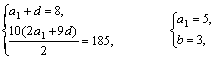
∴a_n=5+3(n-1)，即a_n=3n+2

(2)设b₁=a₂,b₂=a₄,b₃=a₈,b_n=a₂ⁿ=3×2ⁿ+2

∴A_n=(3×2+2)+(3×2²+2)+…+(3×2ⁿ+2)

=3×(2+2²+…+2ⁿ)+2n

=3×+2n

=6×2ⁿ-6+2n

20.（1）证明：在直三棱柱ABC—A₁B₁C₁中，侧棱AA₁⊥平面ABC

∴AA₁⊥BC

又在△ABC中，由AB=2，AC=，∠BAC=30°

∴AC⊥BC

∴BC⊥平面AA₁C，而BC平面A₁BC，

∴平面AA₁C⊥平面A₁BC

（2）解：∵=AA₁·S_△ABC=AA₁××2·sin30°=AA₁=

∴AA₁=3,而BC=1

∴S_侧=（+2+1）×3=9+3

(3)解：作AD⊥A₁C于D

∴平面AA₁C⊥平面A₁BC

∴AD⊥平面A₁BC

∴∠ACD为AC与平面A₁BC所成的角.

又∵AA₁=3

∴tanACD=tanACA₁==

∴所求的角为60°

21.解：设销售总额为y,由已知条件知y=a(1+x%)·b(1-kx%)=ab(1+x%)(1-kx%)

(1)当k=时，

y=ab(1+)(1-)

= (100+x)(200-x)

= (-x²+100x+20000)

x=50时，y_max=ab，即在价格上涨50%时，销售总额最大值为ab.

(2)y=［-kx²+100(1-k)x+10000］定义域为(0,)

由题设知函数y在（0，）内是单调递增函数

∴＞0,0＜k＜1

22.（1）解：设P（x,y），则OP中点为E（）

由

消去y得（2+m²）x²+2mx-1=0

设A(x₁,y₁),B(x₂,y₂)

则=－,

=m+1=

即AB的中点为E（－,）

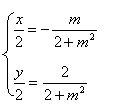于是

消去m,得点P的轨迹方程为2x²+y²-2y=0

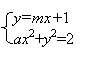(2)证明：由

消去y得

(a+m²)x²+2mx-1=0

进一步就可以求出AB=

∵O到AB的距离d=·S(a)=ABd=

∵a+2m²=1

∴0＜a＜1

∴2＜S(a)＜4