试卷类型：A
高考数学仿真试题(五)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中有一项是最符合题目要求的）
1.已知集合A＝｛y｜y＝log2x，x＞1｝，B＝｛y｜y＝（
）x，x＞1｝，则A∩B等于
A.｛y｜0＜y＜
B.｛y｜0＜y＜1
C.｛y｜＜y＜1＝
D.
2.下列函数中，同时具有性质：①图象过点(0，1) ②在区间(0，＋∞）上是减函数 ③是偶函数，这样的函数是
A.f（x）＝
B.f（x）=log(x+3)
C.f（x）＝
D.f（x）＝3｜x｜
3.已知向量ｍ＝（a，b），向量ｎ⊥ｍ，且｜ｎ｜＝｜ｍ｜，则ｎ的坐标可以为
A.（a，－b） B.（－a，b）
C.（b，－a） D.（－b，－a）
4.方程y2＝ax＋b与y2＝ax2－b表示的曲线在同一坐标系中的位置可以是
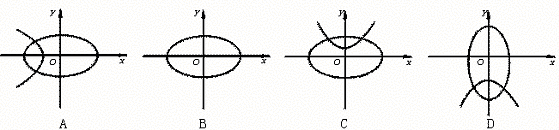
5.函数f（x）＝sin
x＋cos（x－
）的图象相邻的两条对称轴间的距离是
A.3π
B.
C.
D.
6.等差数列｛an｝中，an≠0，若ｍ＞1且am-1－a2m＋am+1＝0，S2m-1＝38，则ｍ的值是
A.38 B.20 C.19 D.10
7.双曲线
的一条准线被它的两条渐近线所截得线段长度恰好为它的一个焦点到一条渐近线的距离，则该双曲线的离心率是
A.3
B.2
C.
D.
8.设a、b、c表示三条直线，
、β表示两个平面，则下列命题中逆命题不成立的是
A.c⊥，若C⊥β，则∥β
B.b
β，c是A在β内射影，若b⊥c，则a⊥b
C.bβ，若b⊥则β⊥
D.b，
，若c∥，则b∥c
9.若方程()x＝有解x0，则x0属于以下区间
A.（0，
） B.（，）
C.（，1）
D.（1，2）
10.已知曲线C1与曲线C：y（x＋a＋1）＝ax2＋a2＋a＋1关于直线y＝x对称，且曲线C1关于点(2，－3)成中心对称图形，则a的值等于
A.－3 B.－2 C.2 D.3
11.不等式①x2＋3＞3x ②a2＋b2≥2（a－b－1） ③
≥2，其中恒成立的是
A.①③ B.②③ C.①②③ D.①②
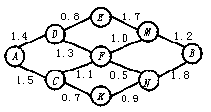12.如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相连，连线上标注的数字表示某信息经过该段网线所需的时间(单位：毫秒).信息由结点A传递到结点B所需的最短时间为
A.5毫秒 B.4.9毫秒
C.4.8毫秒 D.4.7毫秒
第Ⅱ卷(非选择题 共90分)
二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）
13.从6双不同的手套中任取4只，问其中至少有一双配对的概率是 .
14.过点M(1，2)的直线ｌ将圆(x－2)2＋y2＝9分成两段弧，其中的劣弧最短时，ｌ的方程为 .
15.已知数列｛an｝的前ｎ项和为Sn，且Sn＝1＋
，则
.
16.
.
三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）
17.(本小题满分12分)
解不等式
＞
18.(本小题满分12分)
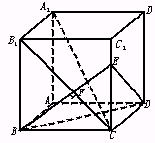已知长方体AC1中，棱AB＝BC＝3，棱BB1＝4，连结B1C，过B点作B1C的垂线交CC1于E，交B1C于F.
(Ⅰ)求证A1C⊥平面EBD；
(Ⅱ)求ED与平面A1B1C1所成角的大小；
(Ⅲ)求棱锥C－BDE的体积.
19.(本小题满分12分)
已知f（x）＝(x－1)2，数列｛an｝是公差为d的等差数列，｛bn｝是公比为q(q∈R且q≠1)的等比数列，设a1＝f（d－1），a3＝f（d＋1），b1＝f（q＋1），b3＝f（q－1）.
(Ⅰ)求数列｛an｝和｛bn｝的通项公式；
(Ⅱ)设数列｛cn｝的前ｎ项和为Sn，如果对一切ｎ∈N，都有
成立，求
.
20.(本小题满分12分)
已知函数
(b＜0)的值域为［1，3］.
(Ⅰ)求实数b、c的值；
(Ⅱ)判断函数f（x）在［－1，1］上的单调性，并给出证明.
21.(本小题满分12分)
某化妆品生产企业为了占有更多的市场份额，拟在2002年度进行一系列促销活动，经过市场调查和测算，化妆品的年销量x万件与年促销ｔ万元之间满足3－x与ｔ＋1成反比例，如果不搞促销活动，化妆品的年销量只能是1万件，已知2002年生产化妆品的设备折旧，维修等固定费用为3万元，每生产1万件化妆品需再投入32万元的生产费用，若将每件化妆品的售价定为：其生产成本的150%“与平均每件促销费的一半”之和，则当年生产的化妆品正好能销完.
(Ⅰ)将2002年的利润y(万元)表示为促销费ｔ(万元)的函数；
(Ⅱ)该企业2002年的促销费投入多少万元时，企业的年利润最大?
(注：利润＝销售收入—生产成本—促销费，生产成本＝固定费用＋生产费用)
22.(本小题满分14分)
已知直线ｌ：y＝ｋx和抛物线C：（y＋1）2＝3（x－1）.
(Ⅰ)ｋ＝－时，求点M(3，0）关于直线ｌ的对称点N的坐标，并判断点N是否在抛物线C上.
(Ⅱ)当ｋ变化(ｋ≠0)且直线ｌ与抛物线C有公共点时，点P(a，0)关于直线ｌ的对称点为Q（x0，y0），请写出x0关于ｋ的函数关系式x0＝f（ｋ），并求出点Q在直线x＝1上时a的取值范围.