高考数学仿真试题一

试卷类型：A　

高考数学仿真试题(一)

 

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.

第Ⅰ卷　(选择题　共60分)

　一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.若函数y=2^ｘ的定义域是P＝｛１，２，３｝，则该函数的值域为

A.｛２，４，６｝　　　　　　　　　　　　　　B.｛２，４，８｝　

C.｛１，０，ｌｏｇ_３２｝ 　　　　　　　　　　D.｛０，１，ｌｏｇ_２３｝　

2.已知函数y=ｓｉｎ（ｘ＋θ）ｃｏｓ（ｘ＋θ）在x=2时有最大值，则θ的一个值是

A. 　　　　　　　　　 B. 　　　　　　　 C. 　　　　　　 D.  

3.经过点(1，0)且垂直于极轴的直线的极坐标方程是

A.ρ＝sinθ　　　　　　　　　　　　　　　　 B.ρ＝cosθ　　

C.ρsinθ＝１　　　　　　　　　 　　　　　　D.ρcosθ＝１ 

4.在等差数列｛ａ_ｎ｝中，若ａ_４＋ａ_６＋ａ_８＋ａ_１０＋ａ_１２＝１２０，则２ａ₁₀－ａ₁₂的

值为

A.20　　　　　　　　　　B.22　　　　　　　　C.24　　　　　　　　D.28　

5.已知（２ｘ^２＋１）^６＝ａ_０＋ａ_１ｘ^２＋ａ_２ｘ^４＋…＋ａ_６ｘ^１２，则ａ_０＋ａ_２＋ａ_４＋ａ_６的值为

A. 　　　　　　　 B.　　　　　　C.　　　　　　D.  

6.一个圆锥被平行于底面的平面截成一个小圆锥和一个圆台，若小圆锥的体积为y，圆台的体积为x，则y关于x的函数图象的大致形状为

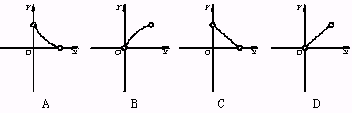
7.把函数y=f(x)的图象沿直线x+y=0的方向向右下方平移2个单位，得到函数ｙ＝ｌｏｇ_２ｘ的图象，则

A.f(x)=log_２（ｘ＋２）＋２　　　　　　　

B.ｆ（ｘ）＝ｌｏｇ_２（ｘ－２）＋２

C.ｆ（ｘ）＝ｌｏｇ_２（ｘ＋２）－２　

D.ｆ（ｘ）＝ｌｏｇ_２（ｘ－２）－２　

8.小王打算用70元购买面值为20元和30元的两种IC电话卡，若他至少买一张，则不同的买法一共有

A.5种　　　　　　　 B.6种　　　　　　　 C.7种 　　　　　　　D.8种　

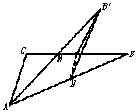
9.已知如图∠Ｃ＝９０°，AC=BC,M、N分别为BC和AB的中点，沿直线MN将△BMN折起，使二面角Ｂ′－MN－Ｂ为60°，则斜线Ｂ′Ａ与平面ABC所成角的正切值为

A. 　　　　　　　　　　　　　　　　 B.

C. 　　　　　　　　　　　　　　　　　 D.  

10.已知函数y=f(x)对任意实数都有f(-x)=f(x),f(x)=-f(x+1)且在［０，１］上单调递减，则

A.ｆ（）＜ｆ（）＜ｆ（）　

B.ｆ（）＜ｆ（）＜ｆ（）

C.ｆ（）＜ｆ（）＜ｆ（）　

D.ｆ（）＜ｆ（）＜ｆ（）　

11.椭圆＝１的焦点Ｆ_１和Ｆ_２，点P在椭圆上，如果线段PＦ_１的中点在y轴上，那么｜ＰＦ_１｜∶｜ＰＦ_２｜的值为

A.７∶１  　　　B.５∶１　　　　　　C.９∶２　　　　　　D.８∶３　

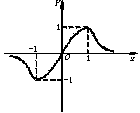12.函数y=的大致图象如图所示则

A.ａ∈（－１，０）　　　　　　　　　B.ａ∈（０，）

C.ａ∈（，１）　　　　　　　　　　D.（１，＋∞）　

第Ⅱ卷　(非选择题　共90分)

二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）

13.sin80°cos35°－sin10°cos55°＝　　　　　　　 .

14.已知抛物线ｙ^２＝ａ（ｘ＋１）的准线方程是ｘ＝－３，那么抛物线的焦点坐标是

　　　　　　 .

15.已知f(x)=a^ｘ（ａ＞１），ｇ（ｘ）＝ｂ^ｘ（ｂ＞１），当f(x_１)＝ｇ（ｘ_２）＝２时，有ｘ_１＞ｘ_２，则ａ、ｂ的大小关系是　　　　  . 

16.设正数数列｛ａ_ｎ｝的前n项和为S_ｎ，且存在正数t，使得对于所有自然数n，有

成立，若＜ｔ，则ｔ的取值范围是　　　　　 .

三、解答题(本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤)

17.（本小题满分12分）

已知π≤θ≤，ｙ＝－３cosθ＋２ｉsinθ.

(Ⅰ)求复数ｚ的模的取值范围；　

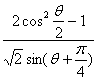(Ⅱ)若argz＝２π－arctg，求的值.　

18.(本小题满分12分)　　　

设两个向量ｅ_１ 、ｅ_２ ，满足｜ｅ_１ ｜＝２，｜ｅ₂ ｜＝１，ｅ_１ ，ｅ₂ 的夹角为60°，若向量2ｔｅ_１　＋７ｅ₂ 与向量ｅ_１ ＋ｔｅ₂的夹角为钝角，求实数t的取值范围.

19.（本小题满分12分）　

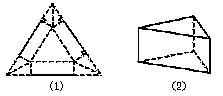
在边长为a的正三角形的三角处各剪去一个四边形，这个四边形是由两个全等的直角三角形组成的，并且这三个四边形也全等，如图（1）若用剩下的部分折成一个无盖的正三棱柱形容器如图（2），则当容器的高为多少时，可使这个容器的容积最大，并求出容积的最大值.

20.（本小题满分12分）　

已知三棱锥P－ＡＢＣ中，PC⊥底面ABC，ＡＢ＝ＢＣ，Ｄ、Ｅ、F分别为AC、PA、PC的中点，DE⊥ＡＰ于E.　

（Ⅰ）求证：ＡＰ⊥平面BDE；

（Ⅱ）求证：平面ＢＤＥ⊥平面ＢＤＦ；　

（Ⅲ）若AE∶ＥＰ＝１∶２，求截面BEF分三棱锥Ｐ－ＡＢＣ所成两部分的体积比.　

 21.(本小题满分14分) 

 设曲线ｃ：ｙ＝ｘ^２（ｘ＞０)上的点Ｐ_０（ｘ_０，ｙ_０)，过Ｐ_０作曲线ｃ的切线与x轴交于Q_１，过Q_１作平行于y轴的直线与曲线c交于P_１（ｘ_１，ｙ_１），然后再过Ｐ_１作曲线c的切线交x轴于Ｑ_２，过Ｑ_２作平行于y轴的直线与曲线c交于Ｐ_２（ｘ_２，ｙ_２），依次类推，作出以下各点：Ｐ_０，Ｑ_１，Ｐ_１，Ｑ_２，Ｐ_２，Ｑ_３…Ｐ_ｎ，Ｑ_ｎ＋１…，已知ｘ_０＝２，设Ｐ_ｎ（ｘ_ｎ，ｙ_ｎ）（ｎ∈N)

(Ⅰ)求出过点Ｐ_０的切线方程；　

(Ⅱ)设ｘ_ｎ＝ｆ（ｎ），求ｆ（ｎ）的表达式；　

(Ⅲ)设Ｓ_ｎ＝ｘ_０＋ｘ_１＋…＋ｘ_ｎ，求Ｓ_ｎ.　　　

22.（本小题满分12分）　　　

已知函数f(x)=－

（Ⅰ）求证：函数y=f(x)的图象关于点（，－）对称；　

（Ⅱ）求f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)的值；　

（Ⅲ）若ｂ_ｎ＝，求证：对任何自然数n，总有ｂ_ｎ＞ｎ^２成立.