高考数学仿真试题(一)A
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至8页。共150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
参考公式:
三角函数的积化和差公式
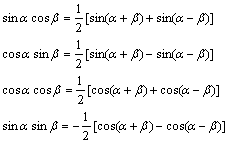
正棱台、圆台的侧面积公式
S台侧=![]() (c′+c)l
(c′+c)l
其中c′、c分别表示上、下底面周长,l表示斜高或母线长
台体的体积公式
V台体=![]()
其中S′、S分别表示上、下底面积,h表示高
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)若集合M={x,y,z},集合N={3,0,-3},f是从M到N的映射,则满足f(x)+f(y)+f(z)=0的映射有
(A)6个 (B)7个 (C)8个 (D)9个
(2)已知集合M={z||z|≤2},N={z|arg(z+1)≤![]() },则M∩N在复平面上对应的图形面积是
},则M∩N在复平面上对应的图形面积是
(A)2π
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)如果函数f(x)是R上的奇函数,在(-1,0)上是增函数,且f(x+2)=-f(x),则下列关系中正确的是
(A)![]()
(B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
(4)使sinx≤cosx成立的x的一个区间是
(A)![]()
(B)
(B)![]()
(C)![]() (D)[0,π]
(D)[0,π]
(5)设函数f(x)=![]() (a为大于1的常数),则使f-1(x)>1的x取值范围是
(a为大于1的常数),则使f-1(x)>1的x取值范围是
(A)![]()
(B)
(B)![]()
(C)![]() (D)(a,+∞)
(D)(a,+∞)
(6)若无穷等比数列{an}的前n项和为Sn,各项和为S,且S=Sn+2an,则
{an}的公比为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
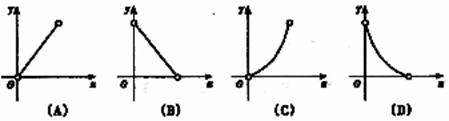
(7)一棱锥被平行于底面的平面截成一个小棱锥和一个棱台,若小棱锥及棱台的体积分别是y和x,则y关于x的函数图象大致形状为
(8)在正三棱锥P—ABC中,E、F分别为PA、AB的中点,∠CEF=90°,若AB=a,则该三棱锥的体积为
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(9)4个茶杯和5包茶叶的价格之和小于22元,而6个茶杯与3包茶叶的价格之和大于24元,则2个茶杯和3包茶叶的价格比较
(A)2个茶杯贵 (B)3包茶叶贵 (C)相同 (D)无法确定
(10)已知圆x2+y2=5x内,过点(![]() )有n条弦的长成等差数列,最短弦长为数列的首项a1,最长弦长为an,若公差d∈(
)有n条弦的长成等差数列,最短弦长为数列的首项a1,最长弦长为an,若公差d∈(![]() ),那么n的值构成的集合为
),那么n的值构成的集合为
(A){6,7,8,9} (B){3,4,5,6}
(C){3,4,5} (D){4,5,6}
(11)已知集合A={1,2,4,8,…,2n}(n≥3,n∈N),集合A中含有三个元素的所有子集依次为B1,B2,…,Bm.若Bi中所有元素之和为ai(i=1,2,…,m)则![]()
(A)2 (B)1 (C)0 (D)不存在
(12)对一切实数x,不等式x4+ax2+1≥0恒成立,则实数a的取值范围是
(A)(-∞,-2) (B)[-2,+∞]
(C)[0,2] (D)[0,+∞]
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内的项目填写清楚。
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)P是以F1、F2为焦点的双曲线上一点,若PF1⊥PF2,且tgPF1F2=![]() ,
,
则双曲线的离心率等于 .
(14)若已知a>b>c,则![]() 的最小值是
.
的最小值是
.
(15)两腰长均是1的等腰Rt△ABC1和等腰Rt△ABC2所在平面成60°的二面角,则两点C1与C2的距离是 .(写出所有可能的值)
(16)已知(1+xi)4n+2(x∈R,i2=-1)展开式中的实数关于x的多项式,则此多项式系数和为 .
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. (17)(本小题满分12分)
设函数![]() ,给出以下四个论断:
,给出以下四个论断:
(Ⅰ)它的图象关于直线![]() 对称;
对称;
(Ⅱ)它的图象关于点(![]() ,0)对称;
,0)对称;
(Ⅲ)它的周期为π;
(Ⅳ)它在区间[-![]() ,0]上是增函数.
,0]上是增函数.
以其中的两个论断为条件,余下的论断为结论,写出你认为正确的两个命题,并对其中一个命题加以证明.
(18)(本小题满分12分)
数列{an}的前n项和为Sn,又数列{bn}满足bn=![]() (r为确定的值),求r的值,并证明{an}是等差数列.
(r为确定的值),求r的值,并证明{an}是等差数列.
(19)(本小题满分12分)
如图,
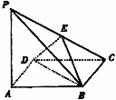
边长为a的菱形ABCD中,A=60°,又PA⊥面ABCD,PA=a,E为CP中点,
(Ⅰ)求证:面BDE⊥面ABCD;
(Ⅱ)求PB与面BDE所成的角大小;
(Ⅲ)求二面角B—DE—C的大小.
(20)(本小题满分12分)
现有流量均为300m3/s的两条河流A、B,汇合于某处后,不断混合,它们的含沙量分别为2kg/m3和0.2kg/m3,假若从汇合处开始,沿岸设有若干个观测点,两股水流在汇经相邻两个观测点的过程中,其混合效果相当于两股水流在1秒钟内交流100m3的水量,即从A股流入B股100m3水,经混合后,又从B股流入A股100m3水并混合. (Ⅰ)问从第几个观测点开始,两股河水的含沙量之差小于0.01kg/m3,(不考虑沙沉淀);
(Ⅱ)随着两股水流的不断混合,它们的含沙量趋向于一个常数,试求出这个常数.
(21)(本小题满分12分)
已知A、B是椭圆![]() 上的两个点,O为坐标原点.
上的两个点,O为坐标原点.
(Ⅰ)若OA⊥OB,|AB|=![]() ,求直线OA、OB的方程;
,求直线OA、OB的方程;
(Ⅱ)(文科不做,理科做)若OA⊥OB,求△AOB面积的最小值.
(22)(本小题满分14分)
(理科做)设f(x)=ax2+bx+c(a,b,c∈R)在区间[0,1]上恒有f(x)≤1.
(Ⅰ)对所有这样的f(x),求a+b+c最大值;
(Ⅱ)试给出一个这样的f(x),使a+b+c确定达到上述最大值.
(文科做)已知一次函数y=kx+c(c>0),二次函数y=x2的图象交于A、B两点,
(Ⅰ)若k、c为已知常数,求线段AB长度|AB|;
(Ⅱ)若k、c为变动的实数时(c>0),求证:
仅当0<c<1时,有两个k值使|AB|=2.
参考答案
一、选择题
(1)B
 提示:满足3+0+(-3)=0有
提示:满足3+0+(-3)=0有![]() =6个;满足0+0+0=0有1个,由加法原理共有
=6个;满足0+0+0=0有1个,由加法原理共有
6+1=7个.
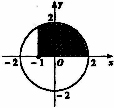
(2)C
提示:满足条件的点集为图中阴影部分,其面积为
![]() .
.
(3)D
提示:因f(x)是(-1,0)上的增函数,且f(x)在R上是奇函数,
∴由f(-x)=-f(x)取x=0得f(0)=0
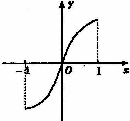 即图象过原点,且f(x)在(0,1)上也是增函数
即图象过原点,且f(x)在(0,1)上也是增函数
又![]()
![]()
即![]()
(4)A
提示:利用单位圆中的三角函数线,画图采用排除法.
(5)A
提示:即求x>1时,y的取值范围
∵![]() 在a>1条件下,是R上递增函数
在a>1条件下,是R上递增函数
∴x>1时,![]()
故原不等式解集为(![]() )
)
(6)B
提示:由S=Sn+2an,S=Sn-1+2an-1
得0=an+2an-2an-1
∴![]()
(7)B
提示:设原棱锥的体积为V,则x+y=V
即y=V-x(0<x<V=,故选B.
(8)B
提示:∵P—ABC为正三棱锥,
∴PB⊥AC,又EF∥PB,∴EF⊥AC
又∠CEF=90°,∴EF⊥CE
∴EF⊥平分PAC,∴PB⊥平面PAC
故PB⊥PA,PB⊥PC,PA⊥PC
∵AB=a,∴PA=PB=PC=![]()
∴VP-ABC=![]()
(9)A
提示:设一个茶杯和一包茶叶的价格分别为x,y元,则有![]()
由②得2x+y>8 ③
由③得-4x-2y<-16 ④
①+④得3y<6
由③得-10x-5y<-40 ⑤
①+⑤得2x>6,故选A
(10)D
提示:∵最长弦为过点(![]() )圆的直径,过点(
)圆的直径,过点(![]() )与最长弦垂直的弦最短.
)与最长弦垂直的弦最短.
∴an=5,a1=4
由an=a1+(n-1)·d,知5=4+(n-1)d
d=![]() ,∴n=4,5,6.
,∴n=4,5,6.
(11)C
提示:∵集合A中含有1的三元子集有![]() 个;同样含有其他任意给定元素的三元子集有
个;同样含有其他任意给定元素的三元子集有![]() 个
个
∴a1+a2+…+an=![]() (1+2+…+2n)=
(1+2+…+2n)=![]() (2n+1-1)
(2n+1-1)
∴原式=0
(12)B
提示:若x=0,不等式恒成立
x≠0时,![]()
∵x2+![]() ≥2,∴a≥-2.
≥2,∴a≥-2.
二、填空题
(13)![]()
提示:设P在右支上,F1为左焦点,且|PF1|=m,|PF2|=n,则
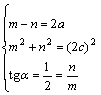 消去m、n得
消去m、n得
![]()
(14)9
提示:∵a>b>c,∴a-b>0,b-c>0,a-c>0
∴a-c-![]()
![]()
(15)![]() .
.
提示:分三种情况讨论.
(16)0
提示:即在(1+xi)4n+2中取x=1考查(1+i)4n+2展开式中的实部,那么由棣模佛定理得(1+i)4n+2=(2i)2n+1=22n+1·(-1)n·i它的实部为0,故所求多项式系数和为0.
三、解答题
(17)两个正确命题为
(Ⅰ)①③![]() ②④
②④
(Ⅱ)②③![]() ①④
①④
(Ⅰ)证明如下:由③函数f(x)周期为π,则ω=2
∴f(x)=sin(2x+φ)
由①函数f(x)的图象关于直线![]() 对称,
对称,
则2×![]() +φ=2kπ±
+φ=2kπ±![]() ,又-
,又-![]() <φ<
<φ<![]()
取k=0,且2×![]() +φ=
+φ=![]() ,得φ=
,得φ=![]() ,
,
∴f(x)=sin(2x+![]() )
)
当x=![]() 时,则f(x)=sin(2×
时,则f(x)=sin(2×![]() +
+![]() )=0
)=0
∴f(x)图象关于点(![]() ,0)对称,即②成立
,0)对称,即②成立
下面证明在[-![]() ,0)上是增函数
,0)上是增函数
由2kπ-![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() (k∈Z时)f(x)分别为增区间,
(k∈Z时)f(x)分别为增区间,
故kπ-![]() (k∈Z)为f(x)的增区间.
(k∈Z)为f(x)的增区间.
取k=0,得[-![]() ,而[-
,而[-![]() ,0
,0![]() [-
[-![]()
∴f(x)在[-![]() ,0]上是增函数.
,0]上是增函数.
(18)由已知有Sn=nran,令n=1,得
a1=S1=ra1![]() (r-1)a1=0
(r-1)a1=0
(Ⅰ)当r=1时,有Sn=nan,再与Sn+1=(n+1)an+1相减,
有an+1=(n+1)an+1-nan
得an+1-an=0
∴r=1时,{an}为常数列,即为等差数列.
(Ⅱ)r≠1时,有a1=0,由a2=S2=2ra2及r为确定值,得r=![]() ,且a2≠0
,且a2≠0
将Sn=![]() nan与Sn+1=
nan与Sn+1=![]() (n+1)an+1相减,
(n+1)an+1相减,
有2an+1=(n+1)an+1-nan
得![]()
∴![]()
故![]() 时,{an}为首项a1=0,公差为a2的等差数列.
时,{an}为首项a1=0,公差为a2的等差数列.
(19)(Ⅰ)连结AC,记AC∩BD=O,由菱形知
![]()
|
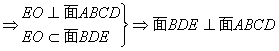
(Ⅱ)设点P到面BDE的距离为d,PB与面BDE所成角为θ,则sinθ=![]() ,
,
而PA∥EO![]() PA∥面BDE,PA⊥面ABCD
PA∥面BDE,PA⊥面ABCD
![]()
![]()
|
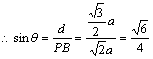
从而PB与面BDE所成角为![]() .
.
(Ⅲ)由(2)知AO⊥面BDE,即CO⊥面BDE,作OH⊥DE于H,连CH,则CH⊥DE,故∠OHC是二面角B′—DE—C的平面角.
在截面△BDE中,易求得DO=![]() 则
则![]()
![]()
又![]()
在Rt△COH中,由tgOHC=![]()
∴二面角B—DE—C大小为arctg![]() .
.
(20)(Ⅰ)设含沙量为akg/m3,bkg/m3的两股水流在单位时间内流过的水量分别为pm3,qm3,则根据化学知识,其混合后的含沙量为kg/m3,又设第n个观测点处A股水流含沙量为ankg/m3,B股水流含沙量为bnkg/m3,(n∈N)
则a1=2,b1=0.2
![]()
即![]()
∴![]() ①
①
![]() ②
②
由①-②得![]()
即数列(an-bn)是以1.8为首项,![]() 为公比的等比数列
为公比的等比数列
∴![]()
由已知an-bn<0.01![]() 2n-1>180
2n-1>180
∴n≥9
即从第9个观测点开始,两股水流的含沙量之差小于0.01kg/m3.
(Ⅱ)由①+②得:an+bn=an-1+bn-1
即{an+bn}是常数列,∴an+bn=2.2 ④
由③+④得![]()
∴![]()
即两股水流含沙量最终趋向于一个常数,这个常数为1.1kg/m3.
(21)(Ⅰ)设OA直线为y=kx,OB直线为y=-![]() ,设A(x1,y1)、B(x2,y2)
,设A(x1,y1)、B(x2,y2)
∵|OA|2+|OB|2=|AB|2
∴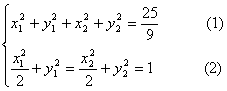
![]() ③
③
由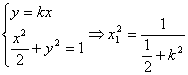
由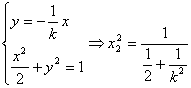 ④
④
将④代入③得:![]()
∴OA、OB方程分别为
![]() ;
;
![]() .
.
(Ⅱ)以x=ρcosθ,y=ρsinθ代入![]()
设A(ρ1,α),则B(ρ2,90°+α)
∴![]()
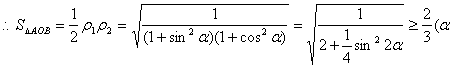 =45°取等号)
=45°取等号)
故OA方程为y=±x时,(S△AOB)min=![]() .
.
(22)(理科做)(Ⅰ)依题设有f(0)=c≤1;f(1)=a+b+c≤1;
![]()
于是a+b=a+b+c-c≤a+b+c+c≤2
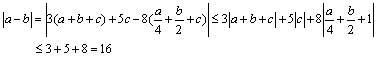
从而ab≥0时a+b=a+b
∴a+b+c=a+b+c≤2+1=3.
当ab<0时,a+b=a-b
∴a+b+c=a-b+c≤16+1=17
即max{a+b+c}=17
(Ⅱ)取a=8,b=-8,c=1时,
![]()
∴当x∈[0,1]时有|8x2-8x+1|≤1
此时a+b+c=8+8+1=17.
(文科做)(Ⅰ)将y=kx+c代入y=x2中得:x2-kx-c=0
设A(x1,y1),B(x2,y2)![]() x1+x2=k,x1x2=-c
x1+x2=k,x1x2=-c
![]()
(Ⅱ)令![]()
![]() ①
①
Δ=16c2-8c+17恒大于0,①永远有解
且![]()
①当c∈(0,1)时
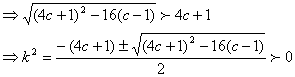
必存在两个k满足上式
②当c=1时,k2=0![]() k=0仅一个k值
k=0仅一个k值
③当c>1时,![]()
![]()
无解,故命题成立.