高考数学仿真试题(一)C

试卷类型：A

高考数学仿真试题(一)C

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.

第Ⅰ卷(选择题  共60分)

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.

3.考试结束，监考人将本试卷和答题卡一并收回.

一、选择题（本大题共12小题，每小题5分，共60分.在每小题的四个选项中，只有一项是符合题目要求的）

1.A、B是x轴上两点，点P的横坐标为2，且｜PA｜=｜PB｜，若直线PA的方程为x－y+1=0，则直线PB的方程为

A.2x－y－1=0　　　B.x+y－5=0　　　 C.2x+y－7=0　　　D.2y－x－4=0

2.已知函数y=f(x)，x∈｛1,2,3｝,y∈｛－1,0,1｝,满足条件f(3)=f(1)+f(2)的映射的个数是

A.2　　　　　　 B.4　　　　　　 C.6　　　　　　 D.7

3.若直线a⊥b，且a∥平面α，则直线b与平面α的位置关系是

A.bα　　　　　　　　　　　   B.b∥α

C.bα或b∥α　　　　　　　　  D.b与α相交或b∥α或bα都有可能

4.函数y=｜tanx｜·cosx(0≤x＜,且x≠)的图象是

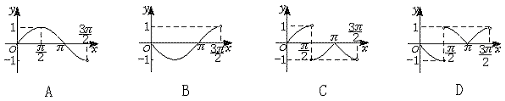
5.在5张卡片上分别写着数字1、2、3、4、5，然后把它们混合，再任意排成一行，则得到的数能被5或2整除的概率是

A.0.8　　　　　　 B.0.6　　　　　　 C.0.4　　　　　　 D.0.2

6.已知奇函数f(x)、g(x),f(x)＞0的解集为（a²,b）,g(x)＞0的解集为（,），＞a²,则f(x)g(x)＞0的解集是

A.（,）　　　　　　　　　　　  B.(－b²,－a²)

C.(a²,)∪(－,－a²)　　　　　　  　 D.(,)∪(－b²,－a²)

7.若O为坐标原点，抛物线y²=2x与过其焦点的直线交于A、B两点，则·等于

A.　　　　　　 B.－　　　　　　 C.3　　　　　　 D.－4

8.已知双曲线－=1的左支上有一点M到右焦点F₁的距离为18，N是MF₁的中点，O为坐标原点，则｜ON｜等于

A.4　　　　　　　　 B.2　　　　　　　　　C.1　 　　　　　　D.

9.函数f₁(x)=,f₂(x)=,f₃(x)=,f₄(x)=的图象分别是点集C₁，C₂，C₃，C₄，这些图象关于直线x=0的对称曲线分别是点集D₁，D₂，D₃，D₄，现给出下列四个命题，其中，正确命题的序号是

①D₁D₂;　②D₁∪D₃=D₂∪D₄；  ③D₄D₃;　④D₁∩D₃=D₂∩D₄

A.①③　　　　　　 B.①②　　　　　　 C.③④　　　　　　 D.②④

10.某科技小组有6名同学，现从中选出3人去参观展览，至少有1名女生入选时的不同选法有16种，则小组中的女生数目为

A.2　　　　  　　　 B.3　 　　　　　　 C.4　　　　　 　　D.5

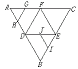11.如图，在正三角形ABC中，D，E，F分别为各边的中点，G，H，I，J分别为AF，AD，BE，DE的中点.将△ABC沿DE，EF，DF折成三棱锥以后，GH与IJ所成角的度数为

A.90°　　　　　 　　　　　　　　　　　B.60°

C.45°  　　　　　　　　　　　　　　　 D.0°

12.设n为满足++2+…+n＜450的最大自然数，则n等于

A.4　　　　 　　　　B.5　　　　　　　　 C.7　　　　　　　 D.6

第Ⅱ卷(非选择题  共90分)

注意事项：

1.第Ⅱ卷，用钢笔或圆珠笔直接答在试题卷中.

2.答卷前将密封线内的项目填写清楚.

题号	二	三						总分
		17	18	19	20	21	22
分数

二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）

　　　　　　　　　　　  x+y≤4,

13.平面内满足不等式组　 x+2y≤6,  的所有点中，使目标函数Z=5x+4y取得最大值的

x≥0,

y≥0

点的坐标是___________.

14.某邮局现只有邮票0.6元，0.8元，1.1元的三种面值邮票，现有邮资为7.50元的邮件一件，为使粘贴的邮票张数最少；且资费恰为7.50元，则至少要购买___________张邮票.

15.抛物线的准线为y轴，焦点运动的轨迹为y²－4x²+8y=0(y≠0),则其顶点运动的轨迹方程为___________________________.

16.在某报《自测健康状况》的报道中，自测血压结果与相应年龄的统计数据如下表.观察表中数据的特点，用适当的数填入表中空白（_________）内.

年龄（岁）	30	35	40	45	50	55	60	65
收缩压（水银柱毫米）	110	115	120	125	130	135	（_______）	145
舒张压（水银柱毫米）	70	73	75	78	80	83	（_______）	88

三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）

17.（本小题满分12分）

已知函数f(x)=2acos²x+bsinxcosx,且f(0)=2,f()=+.

(1)求f(x)的最大值与最小值；

（2）若α－β≠kπ,k∈Z,且f(α)=f(β),求tan(α+β)的值.

18.（本小题满分12分）

已知数列｛a_n｝为等差数列，公差为d，｛b_n｝为等比数列，公比为q，且d=q=2,b₃+1=a₁₀=5,设c_n=a_nb_n.

(1)求数列｛c_n｝的通项公式；

(2)设数列｛c_n｝的前n项和为S_n,求的值.

19.（本小题满分12分）

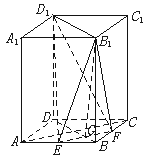
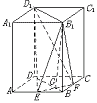如图，正四棱柱ABCD－A₁B₁C₁D₁中，底面边长为2，侧棱长为4.E、F分别为棱AB、BC的中点，EF∩BD=G.

（1）求证：平面B₁EF⊥平面BDD₁B₁；

（2）求点D₁到平面B₁EF的距离d；

（3）求三棱锥B₁－EFD₁的体积V.

2０.（本小题满分12分）

某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时，可全部租出.当每辆车的月租金每增加50元时，未租出的车将会增加一辆.租出的车每辆每月需要维护费200元.

（1）当每辆车的月租金为3600元时，能租出多少辆车？

（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少元？

21.（本小题满分12分）

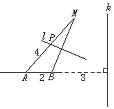如图，A、B是两个定点，且｜AB｜=2，动点M到A点的距离是4，线段MB的垂直平分线l交MA于点P，直线k垂直于直线AB，且B点到直线k的距离为3.

（1）求证：点P到点B的距离与点P到直线k的距离之比为定值；

（2）若P点到A，B两点的距离之积为m，当m取最大值时，求P点的坐标；

（3）若｜PA｜－｜PB｜=1，求cosAPB的值.

22.（本小题满分14分）

定义在（－1，1）上的函数f(x)满足：

①对任意x,y∈(－1,1),都有f(x)+f(y)=f();

②当x∈(－1,0)时，有f(x)＞0.

（1）判定f(x)在（－1，1）上的奇偶性，并说明理由；

（2）判定f(x)在（－1，0）上的单调性，并给出证明；

（3）求证：f()=f()－f()(n∈N).

数学仿真试题(一)答案

一、选择题

1.B　2.D　3.D  4.C　5.B　6.C  7.B　8.A　9.D  10.A　11.B　12.C

二、填空题

13.（4，0）  14.8　15.y²－16x²+8y=0(y≠0)　16.(140)、（85）

三、解答题

17.解：（1）f(0)=2a=2,∴a=1

f()=+b=+,∴b=2

∴f(x)=2cos²x+sin2x=sin2x+cos2x+1

=1+sin(2x+)

∴f(x)_max=1+，f(x)_min=1－

（2）由f(α)=f(β)得sin(2α+)=sin(2β+)

∵α－β≠kπ,(k∈Z)

∴2α+=(2k+1)π－(2β+)

即α+β=kπ+

∴tan(α+β)=1.

18.解：（1）∵a₁₀=5,d=2,∴a_n=2n－15　

又∵b₃=4,q=2,∴b_n=2^n－1

∴c_n=(2n－15)·2^n－1

(2)S_n=c₁+c₂+c₃+…+c_n,

2S_n=2c₁+2c₂+2c₃+…+2c_n

错位相减，得－S_n=c₁+(c₂－2c₁)+(c₃－2c₂)+…+(c_n－2c_n－1)－2c_n

∵c₁=－13,c_n－2c_n－1=2ⁿ

∴－S_n=－13+2²+2³+…+2ⁿ－(2n－15)·2ⁿ=－13+4(2^n－1－1)－(2n－15)·2ⁿ

=－17+2ⁿ⁺¹－(2n－15)·2ⁿ  ∴S_n=17+(2n－17)·2ⁿ

∴=

=.

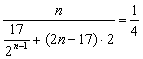19.(1)证明：证法一：

连结AC.

∵正四棱柱ABCD－A₁B₁C₁D₁的底面是正方形，

∴AC⊥BD，又AC⊥D₁D，故AC⊥平面BDD₁B₁.

∵E、F分别为AB、BC的中点，故EF∥AC，

∴EF⊥平面BDD₁B₁，

∴平面B₁EF⊥平面BDD₁B₁.

证法二：

∵BE=BF,∠EBD=∠FBD=45°,

∴EF⊥BD.

又EF⊥D₁D 

∴EF⊥平面BDD₁B₁，

∴平面B₁EF⊥平面BDD₁B₁.

(2)解：在对角面BDD₁B₁中，

作D₁H⊥B₁G，垂足为H.

∵平面B₁EF⊥平面BDD₁B₁，

且平面B₁EF∩平面BDD₁B₁=B₁G

∴D₁H⊥平面B₁EF，且垂足为H，

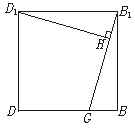∴点D₁到平面B₁EF的距离d=D₁H.

解法一：

在Rt△D₁HB₁中，D₁H=D₁B₁·sinD₁B₁H.

∵D₁B₁=A₁B₁=·2=4,

sinD₁B₁H=sinB₁GB=

==,

∴d=D₁H=4·=.

解法二：

∵△D₁HB₁∽△B₁BG，∴=，

∴d=D₁H===.

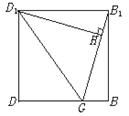解法三：

连结D₁G，则三角形D₁GB₁的面积等于正方形DBB₁D₁的面积即·B₁G·D₁H=B₁B²，

∴d=D₁H==.

（3）解：V= =

=·d·=

20.解：（1）当每辆车的月租金定为3600元时，未租出的车辆数为=12，所以这时租出了88辆车.

（2）设每辆车的月租金定为x元，则租赁公司的月收益为

f(x)=(100－)(x－200),

整理得f(x)=(8000－x)(x－200)=－x²+164x－32000=－(x－4100)²+304200.

所以，当x=4100时，f(x)最大，最大值为f(4100)=304200,

即当每辆车的月租金定为4100元时，租赁公司的月收益最大，最大月收益为304200元.

21.（1）证明：∵PA+PB=AM=4,∴由椭圆定义可知，P点位于以A、B为焦点、长轴长为4的椭圆上，且直线k为该椭圆的准线

∴点P到点B的距离与点P到直线k的距离之比即为e==.

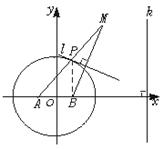（2）解：如图，建立平面直角坐标系，则椭圆的方程为=1,易知，｜PA｜=｜PB｜=2时，

｜PA｜·｜PB｜=m=4为最大，

此时，点P的坐标为（0，±）.

（3）解：∵｜PA｜+｜PB｜=4,｜PA｜－｜PB｜=1,

∴｜PA｜=,｜PB｜=,又∵｜AB｜=2=

∴△PAB是以B为直角的直角三角形　∴cosAPB=.

22.(1)解：当x=y=0时,则f(0)+f(0)=f(0),∴f(0)=0,

f(x)+f(－x)=f(0)=0,即f(－x)=－f(x),∴f(x)在（－1,1）上是奇函数.

（2）解：任取－1＜x₁＜x₂＜0,∵当x∈(－1,0)时，有f(x)＞0.

∴f(x₁)－f(x₂)=f(x₁)+f(－x₂)=f()＞0

即f(x₁)＞f(x₂),∴f(x)在（－1，0）上是减函数.

（3）证明：f()－f()

=f()+f(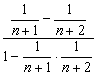－)=f()=f().