高考数学仿真试题(一)答案
一、1.B 2.A 3.D 4.C 5.B 6.C 7.A 8.C 9.B 10.B 11.A 12.B
二、13.
14.(1，0) 15.a＜b 16.（
，＋∞）
三、17.解：(Ⅰ)∵ｚ＝－３cosθ＋２ｉsinθ
∴｜ｚ｜＝
3分
∵π≤θ≤
，∴０≤cos２θ≤１ ∴２≤｜ｚ｜≤３
∴复数ｚ的模的取值范围是［２，３］ 6分
(Ⅱ)由ｚ＝－３cosθ＋２ｉsinθ，得tg（argｚ）＝－
tgθ ８分
而已知argｚ＝２π－arctg
∴－tgθ＝－ ∴tgθ＝
10分
∴
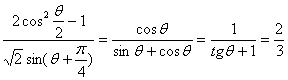１２分
18.解：ｅ１２＝４，ｅ2２＝１，ｅ１·ｅ2＝２×１cos６０°＝１ 2分
∴(2ｔｅ１＋7ｅ2)·(ｅ１＋ｔｅ2)＝２ｔｅ１２＋（２ｔ２＋７）ｅ１·ｅ2＋７ｔｅ２２＝
２ｔ２＋１５ｔ＋７ 6分
∴２ｔ２＋１５ｔ＋７＜０ ∴－７＜ｔ＜－ ８分
设２ｔｅ１＋７ｅ2＝λ（ｅ１＋ｔｅ2）(λ＜０)
10分
∴ｔ＝－
时，２ｔｅ１＋７ｅ2与ｅ１＋ｔｅ2的夹角为π 11分
∴ｔ的取值范围是（－７，－）∪（－，－） １２分
19.解：设容器的高为x，则容器底面正三角形的边长为a-2
ｘ 2分
∴Ｖ（ｘ）＝
ｘ·（A－２ｘ）２（０＜ｘ＜
） 4分
＝·
·４×（a－２ｘ）（a－２ｘ）≤
10分
当且仅当4x=a-2x,即x=
时，
Vmax=
12分
答：当容器的高为时，容器的容积最大，最大值为.
20.（Ⅰ）证明：∵PC⊥底面ABC，BD
平面ABC，
∴PC⊥BD，由AB＝BC，D为AC的中点，
得BD⊥AC，又PC∩AC＝C，∴BD⊥平面PAC 2分
又PA平面PAC，∴BD⊥PA，由已知DE⊥PA，PE∩BD＝D，
∴AP⊥平面BDE 4分
(Ⅱ)证明：由BD⊥平面PAC，DE平面PAC，得BD⊥DE，由D、F分别为AC、PC的中点
∴DF∥AP，又由已知DE⊥AP，∴DE⊥DF 6分
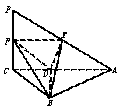BD∩DF＝D，∴DE⊥平面BDF，又DE平面BDE，∴平面BDE⊥平面BDF
8分
(Ⅲ)解：设点E和点A到平面PBC的距离分别为ｈ１和ｈ２
则ｈ１∶ｈ２＝ＥP∶AP＝２∶３ 9分
∴
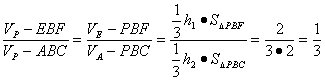11分
所以截面BEF分三棱锥P－ABC所成两部分体积比为１∶２或（２∶１） 12分
21.解：(Ⅰ)∵Ｋ０＝２ｘ０＝４，∴过点P０的切线方程为４ｘ－ｙ－４＝０ 4分
(Ⅱ)∵Ｋｎ＝２ｘｎ，∴过Pｎ的切线方程为
ｙ－ｘｎ２＝２ｘｎ（ｘ－ｘｎ） 6分
将Qｎ＋１（ｘｎ＋１，０）的坐标代入方程得：
－ｘｎ２＝２ｘｎ（ｘｎ＋１－ｘｎ）
∴ｘｎ＋１＝
8分
故｛ｘｎ｝是首项为ｘ０＝２，公比为的等比数列
∴ｘｎ＝f(n)=2·（）ｎ，即f(n)＝（）ｎ－１ 10分
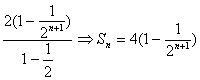
(Ⅲ)Ｓｎ＝
∴
Sn=4(1-
)=4 14分
22.(Ⅰ)证明：设P(x,y)是y=f(x)的图象上任意一点，关于（，－）对称点的坐标为（１－ｘ，－１－ｙ） 2分
由已知y=－
则－１－ｙ＝－１＋＝－
,f(1-x)＝
－
∴－１-ｙ＝f（１－ｘ），即函数ｙ＝f（ｘ）的图象关于点（，－）对称. 4分
(Ⅱ)解：由(Ⅰ)有f(1-x)=-1-f(x)即f(x)+f(1-x)=-1
∴f(-2)+f(3)=-1,f(-1)+f(2)=-1,f(0)+f(1)=-1
则f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)=-3 8分
(Ⅲ)证明：bｎ＝
bｎ＝３ｎ 9分
不等式bｎ＞ｎ２即为３ｎ＞ｎ２
下面用数学归纳法证明
当n=1时，左＝３，右＝１，３＞１不等式成立
当n=2时，左＝９，右＝４，９＞４不等式成立
令n=k(k≥２）不等式成立即３ｋ＞ｋ２
则ｎ＝ｋ＋１时，左＝３ｋ＋１＝３·３ｋ＞３·ｋ２
右＝（ｋ＋１）２＝ｋ２＋２ｋ＋１
∵３ｋ２－（ｋ２＋２ｋ＋１）＝２ｋ２－２ｋ－１＝２（ｋ－）２－
当ｋ≥２，ｋ∈N时，上式恒为正值
则左＞右，即３ｋ＋１＞（ｋ＋１）２，所以对任何自然数n，总有３ｎ＞ｎ２成立，即对任何自然数n，总有bｎ＞ｎ２成立 12分