|
|
学科：数学 |
| 教学内容：第五章 复数 |
一、考纲要求
1.理解复数、虚数、纯虚数的概念以及复数相等的概念，掌握复数的代数形式及其运算法则 ，能正确地进行复数代数的运算。
2.掌握复数三角形式及其特征，三角形式与代数形式的互化；能熟练运用复数的三角形式进行复数的乘、除法及乘方、开方运算。
3.理解复数的模、辐角、辐角主值和共轭复数的概念，掌握相关性质，能运用它们解决相关 的复数问题。
4.理解复数的几何表示及向量表示，掌握复数加法、减法、乘法的几何意义，并能运用它们 解决一些复数问题，会计算平面上两点间的距离。
5.掌握复平面上点的轨迹方程的复数表示形式，会运用复数有关性质求点的轨迹方程。
6.掌握一元二次方程、二项方程在复数集上的解法，某些复系数方程和含有参数的方程的解 法；韦达定理、实系数方程的虚根成对等性质及应用。
二、知识点、能力点提示
复数是一个重要内容，解决复数问题，通常是运用代数形式把它转化为实数问题去解决；运 用三角形式把它转化成三角问题去解决；运用向量及其几何形式把它转化为平面几何问题或 解析几何问题去解决，有时需要运用复数本身一些特有形式如共轭运算，模运算等。复数沟 通了代数、三角、几何之间的联系，因而复数问题的解法往往综合性强且构思巧妙，方法灵 活，复数运算中，求值是最常见的，不仅要用到复数的几种形式，而且有时需运用代数中的 换元法及整体变形，或综合运用其他知识，如：求最值常用基本不等式，函数方法，复数还 常用到数列，二项式定理等知识。
复数的运算种类虽多，但各种运算方式间有联系，最本质的运算方式是代数形式的运算。 多样性的运算使我们研究复数问题时有多种可考虑的途径，以便从中选择较好的方式，运算 常用的结论：
1.(1+i)2=2i,(1-i)2=-2i (a+bi)+(a-bi)=2a (a,b
R)
(a+bi)(a-bi)=a2+b2 (a+bi)2=a2-b2+2abi (a,bR)
(a-bi)2=a2-b2-2abi (a,bR)等
2.i4k=1,i4k+1=i,i4k+2=-1,i4k+3=-i (bN)
3. Z+
=2ReZ
Z-=2(ImZ)i(其中ReZ,ImZ分别表示复数Z的实部和虚部)
4.Z·=｜Z｜2=｜｜2
5.设w=-
+
i 则w3=1,1+w+w 2=0,
=w2=
6.
(Z2≠0)
7.｜Z1·Z2｜=｜Z1｜·｜Z2｜ ｜
｜=
(Z2≠0)
8.Z=
ZR
9.Z=-Z=ki(kR) 
=Z
10.［r1(cosθ1+isinθ1)］［r2(cosθ2+isinθ2)］…［rk(cosθk+isinθk)］
=r1r2r3…rk［cos(θ1+θ2+θ3+…+θk)+isin(θ1+θ2+θ3+… +θk)］
其中r1r2r3…rk≥0 (θ1、θ2、θ3…θk εR)
这些知识点沟通了复数与实数之间的联系，将复数问题化为实数问题解决，训练学生的化归 思想，同时，在处理数据关系时，会根据法则、公式正确地进行运算，而且能根据题目寻求 合理、简捷的运算途径，培养学生的思维能力和运算技能。复数的运算主要是数与式的组合 变形和分解变形，很好的培养了学生的运算能力。
复数的几何意义包括两方面内容，一方面是复数与复平面上的点，复数与复平面上从原点出 发的向量间的一一对应；另一方面是加、减、乘、除、乘方、开方的几何意义。加法的几何
意义：设
，
各与复数Z1，Z2对 应 ，以，为边的平行四边形的对角线 
就与Z1+Z2对应。
减法的几何意义：设，各与复数Z 1，Z2对应，则图中向量
所对应的复数就是Z2-Z1。
｜Z1-Z2｜的几何意义是分别与Z1，Z2对应的两点间的距离。
乘法的几何意义：
设
表示复数r(cosθ+isinθ)(r＞0)，把绕A点按逆时针方向旋转α角，旋转后再把所得向量的长度变为原来的k倍(k＞0)得到
，则对应的复数是［r(cosθ+isinθ)］·k( cosα+isinα)，如果把绕A点按顺时针方向进行同样方式的旋转 和伸缩，那么所得向量对应的复数是［r(cosθ+isinθ)］·k(cosα-isinα)
除法是乘法的逆运算，除法也可表现为乘法的形式，Z1÷Z2=Z1·(
)因此除法运算的几何意义与乘法运算的几何意义实质相同。
复数方根的几何意义：
设对应的复数是Z，Z的n次方根(n≥2,nN)对应于 从原点出发且在 原点处n等分圆周角的n个向量，这n个向量的模都是
，其中一个向量的辐角是复数Z的辐角的n分之一，图中画出了模为8的向量
所对应的复数的三次方根，，
其中的辐角取辐角的三分之一。
理解复数运算的几何意义，通过图形来讨论代数问题，掌握数形结合这一重要的思想方法。
数学是揭示客观事物的数量和形体的本质关系和联系的科学，从认识的角度考虑“数”与“ 形”是事物的两个侧面，数形结合正是从这两个方面去认识事物的特征。
在解决数学问题时，通过数形结合，可将抽象的数学语言与直观的图形相结合，使抽象思维与形象思维相结合，通过图形，发挥直观对抽象的作用，实现抽象概念和具体形象的联系，可以把数量关系转化为图形的性质来研究，或者把图形的性质问题转化为数量关系的问题。
由复数的几何意义推导的下列结论对数形结合思想的培养很有帮助。
1.Z1·Z2≠0，则｜Z1+Z2｜=｜Z1-Z2｜=λi (λ
R且λ≠0)对应的向量⊥
2.设P点对应的复数为Z1，点Q对应的复数为Z2，则向量
对应的 复数是Z2-Z1
3.向量绕点P顺时针方向旋转角θ(θ＞0)所得到的向量对应的复数 应是(Z2-Z1)［cos(-θ)+isin(-θ)］而旋转之后点Q对应的复数应是(Z 2-Z1)［cos(-θ)+isin(-θ)］+Z1
4.｜Z-Z1｜=｜Z-Z2｜表示以复数Z1、Z2在复平面内对应的点为端点的线段垂直 平分线的方程。
5.｜Z-Z0｜=r表示以Z0为复平面内对应的点Z0为圆心，半径是r的圆的方程。
6.｜Z-Z1｜+｜Z-Z2｜=2a(2a＞｜Z1Z2｜)表示以Z1、Z2在复平面内对应的点Z 1、Z2为焦点，，长轴是2a的椭圆方程。
7.｜Z-Z1｜-｜Z-Z2｜=2a(2a＜｜Z1Z2｜)表示以Z1、Z2在复平面内对应点Z1 、Z2为焦点，实轴长是2a的双曲线方程，在复数集上的方程主要有三个问题：①复数集上 方程的求解；②根据方程解的情况讨论参数的取值范围；③与复数集上方程有关的计算或证 明。
求解复数集上的方程主要有以下四种解法：①设Z=x+yi(x，yR)从而转 化为关于实数x，y的方程。
②若是复数集上的二次方程，则可以直接利用二次方程的求根公式，但要注意判别式Δ＜0 ，则x1，2=
③考虑复数的几何意义，结合图形去分析。
④以复数的模为突破口，即着眼于｜Z｜，再求Z。
由复数集上的方程培养学生分类讨论，函数与方程思想的重要数学思想方法，从而培养分析问题，解决问题的能力。
复数的模及有关性质，一般是求模的取值范围或最值，通常有以下四种方法：
①利用复数的三角形式，转化为求三角函数式的最值问题。
②利用不等式｜｜Z1｜-｜Z2｜｜≤｜Z1+Z2｜≤｜Z1｜+｜Z2｜
③考虑复数的几何意义转化为复平面上的几何问题。
④转化为实数范围内的最值问题。
通过这些知识点，利用换元法，待定系数法，训练学生变换与转化思想，培养逻辑思维能力 。
【同步达纲练习】
1.复数Z=
+(m2-2m-15)i，求实数m，使(1)Z是实数；(2)Z 是纯虚数；(3)Z所对应的点在复平面的第二象限；(4)Z是复数；(5)是否存在实数m，使argZ =
知识点：复数的基本概念：实数、纯虚数、虚数、复数、辐角主值，复数所对应的点所在象 限。
能力点：识记能力，计算能力。
2.计算S=1-3i+5i2-7i3+…-99i49
知识点：数列求和公式及方法，复数的四则运算。
能力点：运算能力，逻辑推量能力。
3.设f(Z)=1-，Z1=2+3i，Z2=5-i，试求：
(1)f
(2)f(
)
知识点：函数的有关性质，共轭复数的有关性质：，=Z，(
)
能力点：整体思想，运算能力
4.复数Z=cosθ+isinθ,0＜θ＜π，复数W=
，求argw的最小值。
知识点：复数的辐角主值，乘、除法法则，正切函数单调性，函数最小值的求法，反三角函 数。
能力点：化归思想，逻辑推理能力，运算能力。
5.已知Z=cosθ+isinθ(0＜θ＜2π),w=
求argw及｜w｜
知识点：复数的辐角主值、模、三角变形。
能力点：分类讨论，逻辑推理能力，运算能力。
6.已知Z+(3+
i)Z+(3-i) +9=0求
①｜2Z-2i｜的最大值与最小值
②argZ的最大值与最小值及相应的复数Z。
知识点：共轭复数的性质Z+=2R(Z),Z-=2Im(Z)
(Z１＋Ｚ２)（
）=｜Z１＋Ｚ２｜２
｜Z｜=r (r≠0)=
等
求复数模的最值的三种方法：函数法、不等式法、几何法，运用模、辐角主值的几何意义解 题，复数的代数、几何三角、整体形式间的相互转换。
能力点：数形结合思想，转化与化归思想，逻辑推理能力。
7.设Z1=cosθ+isinθ,Z2=cosθ-isinθ θ∈［
π,
π］,求arg(Z1+2Z2)的最值。
知识点：复数的辐角主值，正切函数的单调性。
能力点：转化与化归思想，运算能力。
8.设z是虚数，ω=z+
是实数，且-1＜ω＜2。
(1)求｜z｜的值及z的实部的取值范围；
(2)设u=
,求证：u是纯虚数；
(3)求ω-u2的最小值。
知识点：复数的模的计算、实部、虚部、纯虚数的概念
能力点：转化与化归思想，运算能力
9.已知复数z=
i,ω=
i,复数
，z２ω３在复平面上所对应的点
分别为P、Q，证明△OPQ是等腰直角三角形(其中O为原点)
知识点：辐角主值，三角的恒等变形，三种形式间的互化。
能力点：数形结合、转化与化归思想。运算能力，逻辑思维能力。
10.设复平面内有一系列向量
(n=1,2,3,4,…)，将逆时针方向旋转θ，且使其模扩大原来的
倍得到
，已知Zn对应向量(n=1,2,3…)Z1= -1+i
(1)当θ=时，求Zn关于n的表达式。
(2)当θ=时，求使Zn为实数时所有n；将所有等于实数的Zn的倒 数按原有次序排列成一个新数列求
(b1+b2+…bn)
(3)当0＜θ＜π时，求｜Z1-Z2｜+｜Z2-Z3｜+…+｜Zn-Zn+1｜
知识点：乘法的几何意义，等比数列，极限。
能力点：转化与化归思想，运算能力，逻辑思维能力。
11.已知Z为虚数，Z+
是实数。
(1)求Z对应复平面内点Z的集合。
(2)设W1=3iZ+1，求复数W1所对应点P的集合。
(3)设W2=
+Z，求复数W2所对应点Q的集合。
知识点：复数的模与共轭，复数减法的几何意义，参数方程，集合，复数的乘、除法。
能力点：数形结合思想，逻辑思维能力。
12.设O为复平面的原点，Z1和Z2为复平面内的两个动点，并且 满足(1)Z1和Z2所对 应的复数的辐角分别为定值θ和-θ(0＜θ＜
＝；(2)△OZ1Z2的面
积为定值S，求△OZ1Z2的重心Z所对应的复数的模的最小值。
知识点：复数与直角坐标系的转化，复数的计算。
能力点：数形结合思想，逻辑思维与运算能力。
13.设复数Z满足2≤Z+
≤10，试求复平面上与复数Z所对应的点的轨
迹。
知识点：复数的共轭的性质，复数与不等式，反三角函数，复数的几何意义。
能力点：逻辑思维能力，分析问题与解决问题的能力。
14.设虚数Z1，Z2满足Z12=Z2。
(1)若Z1，Z2又是一个实系数一元二次方程的两个根，求Z1，Z2
(2)若Z1=1+mi(i为虚数单位)，｜Z1｜≤，复数ω=Z2+3，求｜ω｜ 的取值范围
知识点：复数三角形式的运算，复数的模与共轭，复数乘法的几何意义。
能力点：运算能力，逻辑思维能力。
15.设复数Z=cosθ+isinθ(0＜θ＜π)，W=
并且｜W｜=
,argW＜求θ
知识点：三角恒等变形，复数的模与共轭，复数的辐角主值。
能力点：分类讨论与归纳思想，逻辑思维能力。
16.等比数列｛Zn｝中，已知Z1=1，Z2=a+bi,Z3=b+ai(a,b∈R,a＞0)
(1)求a,b的值；并将Z2表示成三角形式。
(2)求满足Z1+Z2+…+Zn=0的最小自然数n，并计算Z1·Z2…Zn的值。
(3)前100项中有多少项是实数?并求这些实数和。
知识点：等比数列的性质，复数的三角表式。
能力点：转化与化归思想，分析与解决问题的能力。
17.已知复数集合M={Z‖Z-2+i｜≤2 Z∈C}∩{Z‖Z-2-i｜=｜Z-4+i｜ Z∈C}
(1)试在复平面内作集合M的图形并说明图形的名称。
(2)求集合M中元素Z辐角主值的取值范围。
(3)求集合M中元素Z模的取值范围。
知识点：集合、复数减法的几何意义，复数的辐角主值，复数的模，点到直线的距离。
能力点：数形结合思想，逻辑思维能力。
18.已知复数Z1，Z2满足｜Z1｜=｜Z2｜=1且Z1+Z2=+i,求Z1，Z2的值。
知识点：复数的计算，复数转化为另一种表示方法
能力点：分析问题和解决问题的能力
19.已知t∈R，且关于x的方程x2+2x+t=0的两个根为复数α，β求｜α｜+ ｜β｜的值。
知识点：二次方程的判别式，根与系数的关系。
能力点：分类讨论思想，函数与方程思想。
20.设关于x的方程2x2+3ax+a2-a=0至少有一个根的模等于1，试确定实数a的值。
知识点：复数的模，实系数方程的两根以共轭形式出现，根与系数的关系。
能力点：函数与方程思想，分类讨论思想，逻辑思维能力。
21.设α、β为两个虚数，且满足α+β=-3，且｜α｜＋｜β｜=4，试判断cos(argα-argβ )是否存在最大值或最小值，如果不存在，说理理由，如果存在，求出这个最大、最小值。
知识点：复数的转化
能力点：运算能力，逻辑思维能力
22.复数集合中有个一元二次方程，它的二次项是2x2，它的一次项是-x，常数项是实数 ，设α，β是该方程的两个复数根且满足｜α-β｜=，解这个方程。
知识点：二次方程根与系数的关系。
能力点：分类讨论思想。
23.复数Z≠0，｜Z+｜＝1 求证：
≤｜Z｜≤
知识点：复数的模与共轭，不等式的应用。
能力点：逻辑思维能力，运算能力。
24.实系数方程x2-2ax+b=0的两个复数根Z1，Z2在复平面上表示Z1，Z2的点为 直径端点的圆恰好过点P(1，1)，求复数a+bi所表示的点的轨迹方程。
知识点：复数减法的几何意义，二次方程根与系数的关系，虚根的求法。
能力点：分类讨论思想，数形结合思想，分析与解决问题的能力。
25.设0＜θ＜2π，复数Z=1-cosθ+isinθ,μ=a2+ai (a∈R)，且Z·μ是 纯虚数，求复数μ的辐角主值argμ(用θ的代数式表示)
知识点：三角恒等变形，复数的辐角主值
能力点：分类讨论思想，运算能力，逻辑思维能力
参考答案
【同步达纲练习】
1.解：(1)由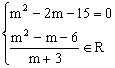
解得m=5
(2)由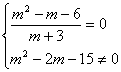
得m=-2 或m=3
(3)由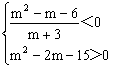
得m＜ -3
(4)由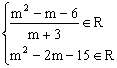
得m≠-3
(5)由=m2-2m-15
m3-20m-39=0
考虑函数f(m)=m3-20m-39(m≠-3)当m→+∞时 f(m)→+∞
当m→-∞时f(m)→-∞可见存在f(m0)=0，使m3-20m-39=0
表明存在实数m，使argZ=
2.解：S=1-3i+5i2-7i3+…+97i48-99i49 ①
iS=i-3i+5i3-…+97i49-99i50 ②
①+②得 (1+i)S=1-2i+2i2-…+2i48-2i49-99i50
=1-2(i-i2+…-i48+i49)-99i2
=1-2·
+99
=100-2
=100-2i
∴S=
=
=49-51i
3.解：
(1)f(
)=1-(
)=1-(Z1-Z2)=1-［(2+3i)-(5
-i)］=4-4i
f()=1-(
)
=1-
=1-
=1-
=
4.解：w=
=
=
∵W的实部
＜0，虚部
＞0可见＜argw＜π，tg(argw)=
(0＜θ＜π
在(，π)上，函数y=tgx是增函数，要求argw的最小值，先求tg(argw)的最小值，即求y=的最小值。
5sinθ=ycosθ-5y 5y=ycosθ-5sinθ=
·cos(θ+t)
其中cost=
sint=
∵y＜0
∴t为第二象限的一个角 设t=arccos
∵｜cos(θ+t)｜=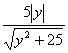
≤1
∴25y2≤y2+25
∴y2≤
∴-
≤y≤0
∴θ＝π-arccos，则 y=tg(argw)=-
∴argw=arctg(-
)
∴argw的最小值为arctg(-)
解法二：由Z=cosθ+isinθ(0＜θ＜π＝得Z=x+yi,x2+y2=1,x＜0,y＞0
W=
=
=
=
=
tg(argw)=
问题转化为求函数t＝，x2+y2＝1，x＞0，y＞0的最小值
将y＝
x-t，代入x2＋y2＝1 整理得
(1+
)x2-
x+t2-1＝0
∵x∈R
∴(-
)2-4(1+)·(t2-1)≥0
∴t2≤
5.解法一：∵｜Z｜＝1，∴Z＝1
W＝＝1+Z+Z2＝Z+Z+Z2＝Z(Z++1)
＝(2cosθ+1)(cosθ+isinθ)
∵θ＜(0，2π) 于是
当2cosθ+1≥0即θ∈(0，
)∪［
,2π］时 argw=0,｜w｜=2cosθ+1
当θ∈(，)时 2cosθ+1 ＜0,w=-(2cosθ+1)［cos(π+θ)+isin(π+θ)］
｜w｜=-［2(cosθ+1)］
由π+θ∈(π+，2π+
)得
若θ∈(,π)则argw=π+θ；若θ［π, )则argw=π+θ-2π=θ-π
解法二：
w=
=
=
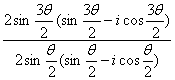
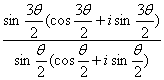
=sin
csc
(cosθ+isinθ)
由∈(0,3π)得当0＜≤π 或2π≤＜3π得θ∈(0,)∪［
π,2π ］时sin≥0rgw=０ ｜w｜=sincsc
当θ∈(
π, )时 ｜w｜=-sincsc
6.解法一：
∵Z+(3+i)Z+(3-i)+9=0
∴(Z+3-i)(Z+3+i)=3 即(Z+3-i ) (
)=3
∴｜Z+3-i｜=
∵｜2Z-2i｜=2｜(Z+3-i)-3｜≤2(｜Z+3-i)｜+｜-3｜=2(+3)
当且仅当 Z+3-i=λ(-3)(λ＜0即
｜Z+3-i｜=｜-3λ｜=-3λ
即-3λ= 即Z=-3++i时 ｜2Z-2i｜的最大值为2(+3)又｜2Z-2i｜=2｜｜(Z+3-i)｜-3｜≥2(｜｜Z+3-i｜-｜-3｜｜)=2(3-)当且仅当Z+3-i=λ(-3)(λ＞0)即｜Z+3-i｜=｜-3λ｜=3 λ 即3λ= 即Z=-3-+i时，｜2Z-2i｜的最小值为2(3-)
解法二：
由｜Z+3-i｜=知Z对应点在以(-3，)为圆 心，为半径的圆上
∴｜Z-i｜的最大值为
=3+,最小值为
-=3-,从而｜2Z-2 i｜的最大值为2(3+)，最小值为2(3-)
解法三：
由｜Z+3-i｜ 设Z+3-
=(cosθ+sinθ) θ∈［0,2π］则
｜2Z-2i｜=2｜-3+ (cosθ+isinθ)｜
=2
=2
∴｜2Z-2i｜的最大值为2·
=2(3+)
最小值是2=2(3-)
②由①设OA，OB分别与圆C相切于A、B两点，则argZ的最大值与最小值分别是B、A对应复数Z 1，Z2的辐角主值
∵｜OC｜=2,∴∠AOC=∠BOC=
∴argZ的最大值为π，最小值为π-2·=， 对应的复数
Z1=
(cos+isin
)=-+
i Z2=-3
7.解：∵Z1+2Z2=(sinθ+2cosθ)+i(sinθ-2cosθ)
∴tg［arg(Z1+2Z2)］=
=
=1-
又θ∈［π,
π］
∴tgθ∈［-1,1］1-∈［-3,- 
］
又sinθ+2cosθ＜0,sinθ-2cosθ＞0
∴arg(Z1+2Z2)
∈［,π］
又tgx在(，π)上单调递增
∴arg(Z1+2Z2)的最小值为argctg(-3)+π=π-arctg3
最大值为arctg(-)+π=π-arctg
8.解 (1)z=x+yi,x∈R,y∈R,且x≠0
则 ω=x+yi+
=x+yi+
=(x+
)+(y-
)i
由ω∈R，得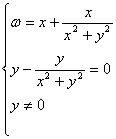
x2+y2=1
于是ω=2x,由-1＜ω＜2,得-＜x＜1
故｜z｜=1,z的实部的取值范围是(-，1)
(2)由(1)知｜z｜=1，可设z=cosθ+isinθ
而u=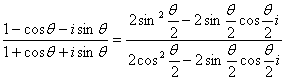
=tg·
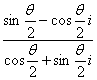=tg (sin-cosi)(cos-sini)
=tg (-cos２-sin2)i=-tgi
若tg=0,则sin=0，那么z=cosθ∈R与已知z虚矛盾
故u是纯虚数
(3)设z=cosθ+isinθ,则ω=2cosθ,u=-tgi
ω-u2=2cosθ+tg2,令t=tg2则
ω-u2=
+t=
=t-2+
=(t+1)+ -3≥4-3=1
故ω-u2的最小值是1
9.解法一 z=i=cos(-)+isin( -)
ω=
+i=cos+isin
得zω=cos
+isin
=cos(-)+isin(-)
z２ω3=(cos(-)+isin(-))×(cos
+isin)
=cos
+isin
因 OP与OQ的夹角为-(-)=
所以 OP⊥OQ
又｜OP｜=｜｜=1,｜OQ｜=｜z２ω３｜=1
则｜OP｜=｜OQ｜
由此知△OPQ有两边相等且其夹角为直角，故△OPQ为等腰直角三角形。
解法二 因z=
i=cos(-)+isin( -)
得z3=-i
因ω=i=cos+isin
得ω4=-1
则
·
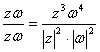=i
所以OP⊥OQ，｜OP｜＝｜OQ｜
故△OPQ有两边相等且其夹角直角，故△OPQ为等腰直角三角形。
10.解：
(1)Z1=(cosπ+isinπ) Zn=Zn-1(cos+isin)(n≥2)
∴Zn=Z1［(cos+isin)］n-1
=2
(cos
π+isinπ)
=2(-sin
+icosπ)(n =1,2,3…)
(2)Zn为实数cosπ=0
π=kπ+n=4k+2 (k∈Z)由n∈N知k=1,2,3……时Z n为实数
∴b1=
,
=
∴bn=-(-
)n-1
∴(b1+b2+…bn)=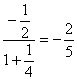
(3)∵｜Zn+1-Zn｜=｜Zn｜·｜(cos+isin)-1｜=2
∴｜Z1-Z2｜+｜Z2-Z3｜+…+｜Zn-Zn+1｜=+()2…+()n
=(2+)(2-1)
11.解：
(1)∵Z+∈R ∴Z+=(
) 即
=0
又Z为虚数 ∴Z-≠0,∴Z=4即｜Z｜=2其中Z≠±2
∴点Z的集合是圆心在原点，半径是2的圆且去掉点(±2，0)
(2)由w1=3iZ+1Z=
(w1-1)(-i)
代入｜Z｜=2 得｜w1-1｜=6 又Z≠±2
∴W1≠1±6i
∴点p的集合是以(1，0)为圆心，6为半径的圆，且去掉点(1，±6)
(3)由｜Z｜=2,且Z≠±2,设Z=2(cosθ+isinθ) θ∈(0,π)∪(π,2π) w2=x+yi(x,y∈R) 则
x+yi=2(cosθ+isinθ)+
=
cos θ+isinθ
∴
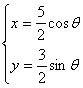消去θ得
x2+
y2=1，其中x∈(-,)
即点Q的集合为一椭圆，且去掉在x轴上的两个顶点(±，0)
12.设Z1、Z2和Z点对应的复数分别为z1、z2和z，且z1=r1(cosθ+isinθ)，z 2=r2(cosθ-isinθ)
因Z是△OZ1Z2的重心，由复数加法的几何意义
3z=r1(cosθ+isinθ)+r2(cosθ-isinθ)
=(r1+r2)cosθ+(r1-r2)isinθ
｜3z｜2=(r1+r2)2cos2+(r1-r2)2sin2θ
=r12(cos2θ+sin2θ)+Z22(cos2θ+sin2θ)+2r1r2(cos2θ-si n2θ)
=r12+r22+2r1r2cos2θ
=(r1-r2)2+2r1r2(cos2θ+1)=(r1-r2)2+4r1r2cos2θ ①
又 0＜θ＜，0＜2θ＜π，sin2θ＞0
△OZ1Z2的面积S=OZ1·OZ2sin2θ=r1·r2sin2 θ
得 r1·r2=
②
将②式代入①得：
｜3z｜2=(r1-r2)2+4cos2θ=(r1-r2)2+4Sctgθ
由②和③可知
当r1=r2=
时，｜z｜最小=
13.解法一：设Z=x+yi(x,y∈R)
则Z+=(x+yi)+
=(x+
)+(y-)i
即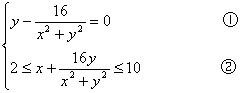
由①得y=0或 x2+y2=16 分别代入②中2≤x≤18或1≤x≤5的轨迹分别为：x轴上连结( 2，0)和(8，0)的一条线段或以原点为圆心，4为半径的圆上的一段圆弧(包括端点)
解法二：
∵Z+∈R
∴Z+=+
∴Z·｜Z｜2+16=·｜Z｜2+16Z
∴｜Z｜2(Z-)=16(Z-)
∴Z=或｜Z｜2=16
由Z=知Z∈R
根据 2≤Z+≤10 知
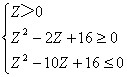∴2≤Z≤8
由｜Z｜2=16知｜Z｜=4 设Z=4(cosθ+isinθ)
由2≤4(cosθ+isinθ)+
≤10
2≤4(cosθ+isinθ)+4(cosθ-isinθ)≤10
≤cosθ≤1
∴2θπ-arccos≤θ≤2θπ+arccos (k∈Z)
∴轨迹方程为
2≤Z≤8
或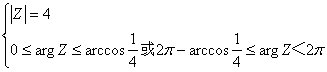
14.解 (1)设z1=a+bi,z2=a-bi(a,b∈R,且b≠0)(因为实系数的一元二次方程的虚根共 轭)
由z12=z2得a2-b2+2abi=a-bi
即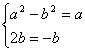
解得
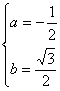和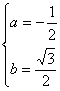
所以z1=-
i,z2=-
i,
(2)由且z1=1+mi,｜z1｜≤且m≠0，得
0＜m2≤1，
又z2=Z12,ω=z2+3，所以ω=(4-m2)+2mi，
｜ω｜=
由0＜m2≤1得，13≤(m2-2)2+12＜16
即
≤ω＜4，故｜ω｜的取值范围是［,4)
15.解法一：
W=
=
=
=
=tg2θ·
=tg2θ(sin4θ+icos4θ)
∵｜W｜=
∴｜tg2θ(sin4θ+icos4θ)｜=｜tg2θ｜=
∴tg2θ=±
∵0＜θ＜π
∴0＜2θ＜2π
当tg2θ=时 θ=或
π此时 w=(cos+isin)
∴argw=＜满足题意。
当tg2θ=-时 θ=
π或
π，此时w=(cos
+isinπ)
此时argw=π＞符合题意。
∴θ=或π
解法二：
∵｜W｜=
∴｜｜=｜｜=｜
｜=
即：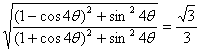
即：
=｜tg2θ｜=
16.解：
(1)∵Z22=Z1Z3
∴(a+bi)2=b+ai即
∵a＞0
∴b=,a=
∴Z2=+i=cos+isin
(2)公比q=Z2=cos+isin 且Sn=0
∴qn-1=0 即cos
+isin=1,n的最小值为 12
此时Z1Z2……Zn=q1+2+…+11=q66=cos
+isin =-1
(3)an=a1qn-1=cos
π+isin π∈R时
sinπ=0,n=6k+1(k为非负整数)
当6k+1≤100时 0≤k≤16 共有17个实数项，它们构成等比数列，首项为1，公比为q 6=-1,17个实数项的和为1。
17.解：(1)集合m的图形是两个图形的公共部分，一个图形是由｜Z-(2-i)｜≤2表示的圆面 ，另一个图形是以点A(2，1)，B(4，-1)为端点的线段的垂直平分线，它们的公共部分是一 条线段，如图中的DE，其方程为x-y-3=0 (2-≤x≤2+)
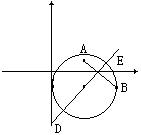
(2)由(1)知E(2+，-1)，tg＜x0E=
=
D(2-,--1)
tg＜xOD=｜
｜=
∴线段DE上的点Z的辐角主值的取值范围
［0,arctg
］∪［2π-arctg，2π］
(3)｜OD｜=
｜OE｜=
原点O到直线x-y-3=0的距离d=
∴线段DE上的点Z的模的取值范围为［
,
］
18.解法一 依题可设z1=cosα+isinα,z2=cosβ+isinβ,不妨设α≤β且α、β∈［0 ，2π)
因 z1+z2=i,得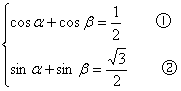
由①2+②2得，cos(α-β)=-,又α,β∈〔0,2π〕
所以α,β=或αβ=
把α=β+代入①、②得cosβ=1,sinβ=0,cosα=-,sinα=
则z1=-+i,z2=1
把α=β+代入①、②得cosβ=-,sinβ=,cosα=1,sinα=0
则z1=1,z2=-+i
所以
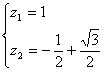或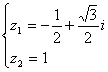
解法二 由｜z1+z2｜=1,得(z1+z2)(
+ 
)=1
展开左边并注意｜z1｜=｜z2｜=1得，
z1
2+z22=-1
所以z12的实部等于z22的实部，等于-
又｜1z2｜=1，从而1z2的虚部为±
得1z2=-±i
则z2=z1·1z2=z1(-±i)
z1+z2=z1+z1(-±i)= ±i
z1=1,z2=-±i
或z1=-±iz2=1
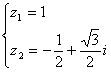或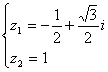
19.解：关于x的二次方程的判别式Δ=4-4t=4(1-t)
(1)当t≤1时，Δ≥0 α=-1-
β=-1+
∴｜α｜+｜β｜=1++｜-1｜
①当t≤0时｜α｜+｜β｜=2
②当0＜t≤1时｜α｜+｜β｜=2
(2)当t＞1时Δ＜0 α=-1-i β=-1+
i
∴｜α｜+｜β｜=
20.解：设α是方程的一个根且｜α｜=1
(1)当α∈R时α=±1 当α=1代入原方程有
a2+2a+2=0 无实解
当α=-1时 代入原方程有a2-4a+2=0解得a=2±
(2)当α为虚数时，
是方程的一个根
由α·=
及｜a｜=1知a2-a-2=0解得a=2或a=-1
又Δ=a2+8a＜0-8＜a＜0
∴a=-1
综上所述 a=-1或a=2±
21.设φ=argα,θ=argβ,｜α｜=r,则有｜β｜=4-｜α｜=4-r,于是由α+β=-3得
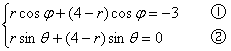
①2+②2，得
cos(φ-θ)=1+
由于0＜r＜4,所以0≤2(r-2)2＜8
所以-8≤2(r-2)2-8＜0
所以，当r=2时，cos(φ-θ)有最大值
cos(φ-θ)没有最小值
22.解：设方程为2x2-x+k=0,k∈R，它的根有两种可能的状况
α，β都是实数；α，β互为共轭虚数。
若方程有二实根，则(-1)2-8k≥0 即k≤
由｜α-β｜=
得k=-
α，β=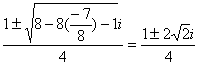
若方程有二互为共轭的虚根，则(-1)2-8k＜0,k＞
由｜α-β｜=
得k=
∴α，β=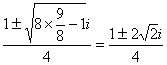
综上所述：当k=-时，方程有二实根，它们是
当k=时，方程有二互为共轭的虚根，它们是
23.解：由｜Z+｜＝1，知｜Z｜=｜Z2+1｜
对｜Z2+1｜可能的不等变形有
｜｜Z2｜-1｜≤｜Z2+1｜≤｜Z2｜+1
即是｜｜Z2｜-1｜≤｜Z｜≤｜Z2｜+1
∴
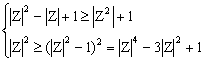
解之得 
≤
≤
即≤｜Z｜≤
方法二：
1＝｜Z+｜≥｜｜Z｜-
｜
∴(｜Z｜-)2≤1
∴｜Z｜2+
-3≤0
∴｜Z｜4-3｜Z｜2+1≤0
方法三：
1＝｜Z+｜2
＝(Z+)(+
)
＝Z·+
+
＝｜Z｜2++()
注意到：-2＝-2｜
｜≤≤2｜
｜＝2
∴｜Z｜2+＝1-()≤1+2 ＝3
∴｜Z｜4-3｜Z｜2+1≤0
24.解：依题意，可设圆的方程为｜Z-
｜=
即 ｜Z-a｜=｜Z1-Z2｜
当Δ≥0 即a2≥b时
∵Z1-Z2为实数
∴｜Z1-Z2｜=
=
=
=2
∴｜Z-a｜=
又∵圆过(1，1)点，代入有｜(1-a)+i｜=
化简整理得 b-2a+2=0(a2≥b)为所求轨迹方程
当Δ＜0即a2＜b时
｜Z1-Z2｜=｜
｜
=｜
｜
=2
∴｜Z-a｜=
又∵圆过点(1，1)，代入有｜(1-a)+i｜=化简整理得
b=2a2-2a+2(a2＜b)为所求轨迹方程。
25.解：∵Z·μ=(1-cosθ+isinθ)(a2+ai)
=［a2(1-cosθ)-asinθ］+［a2sinθ+a(1-cosθ)i］
∵Z·μ是纯虚数
∴
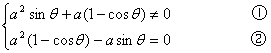
由①2asin(acos+sin)≠0
∴a≠0 且sin≠0
由②2sin (asin-cos)=0
∴asin-cos=0
∴a=ctg (∵a≠0,∴θ≠π)
∴μ=a2+ai=ctg2+ictg=
(cos+i sin)
当0＜θ＜π时0＜＜ 此时 argμ=
当π＜θ＜2π时 ＜＜π
此时μ=-［cos( π+)+isin(π+)］
且π+∈(π,2π)
∴argμ=π+