课时7 复数的有关概念
一.复习目标
了解引进复数的必要性;理解复数的有关概念;掌握复数的代数表示及向量表示。
二.例题讲解
例1.下列四个命题中是真命题的是( D )
A.![]() 的共轭复数是
的共轭复数是![]()
B.若两个复数的差的纯虚数,则它们一定为共轭复数
C.若两个复数的和为实数,则它们为共轭复数
D.若两个虚数的和与积都为实数,则它们为共轭复数
例2.实数![]() 分别取什么数值时,复数
分别取什么数值时,复数![]() 是:(1)实数;(2)虚数;(3)纯虚数;(4)对应点在
是:(1)实数;(2)虚数;(3)纯虚数;(4)对应点在![]() 轴上方;(5)对应点在直线
轴上方;(5)对应点在直线![]() 上。
上。
解:(1)由![]() ,得知:
,得知:![]() 或
或![]() 时,
时,![]() 为实数;
为实数;
(2)由![]() ,得知:
,得知:![]() 且
且![]() 时,
时,![]() 为虚数;
为虚数;
(3)由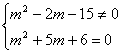 ,得
,得![]() 时,
时,![]() 为纯虚数;
为纯虚数;
(4)由![]() ,得知:
,得知:![]() 或
或![]() ,
,![]() 的对应点在直线
的对应点在直线![]() 上。
上。
例3.设关于![]() 的的方程是
的的方程是![]() ;
;
(1)若方程有实数根,求锐角![]() 和实数根;
和实数根;
(2)证明:对任意![]() ,方程无纯虚根。
,方程无纯虚根。
解:(1)设实数根是![]() ,则
,则![]() ,即
,即![]()
![]() ,∵
,∵![]() 、
、![]() ,
,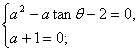
∴![]() 且
且![]() ,又
,又![]() ,∴
,∴![]() ;
;
(2)若有纯虚数根![]() ,则
,则![]() ,
,
∴![]() ,且
,且![]() 这不可能。
这不可能。
例4.已知![]() ,其中
,其中![]() ,且
,且![]() 为纯虚数。
为纯虚数。
(1)求![]() 的对应点的轨迹;
的对应点的轨迹;
(2)求![]() 的最大值、最小值。
的最大值、最小值。
解:设![]() ,则
,则![]()
∵![]() 为纯虚数,∴
为纯虚数,∴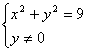
![]() 的对应点的轨迹是以原点为圆心,3为半径的圆,并除去(-3,0),(3,0)两点。
的对应点的轨迹是以原点为圆心,3为半径的圆,并除去(-3,0),(3,0)两点。
(2)由![]() 的轨迹可知
的轨迹可知![]() ∴
∴![]() ,圆心对应
,圆心对应![]() ,半径为3。
,半径为3。
∴![]() 的最大值为9,最小值为3。
的最大值为9,最小值为3。
三、同步练习:《高考三人行—学生用书》P362
课时8 复数的代数形式及其运算
一、复习目标
熟练掌握复数代数形式的加、减、乘、除运算法则,灵活利用![]() 、
、![]() 的性质,或适当变形,创造条件,从而转化为关于
的性质,或适当变形,创造条件,从而转化为关于![]() 、
、![]() 的计算问题,同理要注意复数整体思想的把握以及复数运算几何意义的利用。
的计算问题,同理要注意复数整体思想的把握以及复数运算几何意义的利用。
二、例题讲解
例1.(1)对于![]() ,下列列结论成立的是( D )
,下列列结论成立的是( D )
A.![]() 是零 B.
是零 B.![]() 是纯虚数 C.
是纯虚数 C.![]() 是正实数 D.
是正实数 D.![]() 是负实数
是负实数
(2)![]() 的值为( B
)
的值为( B
)
A.-2 B.0 C.2 D.4
(3)设非零复数![]() 、
、![]() 满足
满足![]() 则代数式
则代数式![]() 的值是( B )
的值是( B )
A.![]() B.-1
C.1
D.0
B.-1
C.1
D.0
(4)已知函数![]() ,则
,则![]() 的值是_____________(
的值是_____________(![]() )
)
例2.设![]() 为虚数单位,复数
为虚数单位,复数![]() 和
和![]() 满足
满足![]() 。
。
(1)若![]() 和
和![]() 又满足
又满足![]() ,求
,求![]() 和
和![]() 的值。
的值。
(2)求证:如果![]() ,那么
,那么![]() 的值是一个常数,并求这个常数。
的值是一个常数,并求这个常数。
解:(1)∵![]() ,∴
,∴![]() ,代入
,代入![]() 得:
得:
![]() 即
即![]() ,
,
设![]() ,则上式可变为:
,则上式可变为:![]() 。
。
∴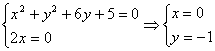 或
或![]() 。
。
∴![]() 或
或![]() 。
。
(2)法一:由![]() 有
有![]()
设![]() ,则有
,则有![]() ,
,
∴![]()
![]() ,
,
∴![]() 的值是一个常数,且等于
的值是一个常数,且等于![]() 。
。
证法二:由![]() 有
有![]()
![]() ,
,
所以,![]() ,以下同上。
,以下同上。
例3.设![]() 是虚数,
是虚数,![]() 是实数,但
是实数,但![]() ,
,
(1)求![]() 的值及
的值及![]() 的实部的取值范围;
的实部的取值范围;
(2)设![]() ,求证:
,求证:![]() 为纯虚数;
为纯虚数;
(3)求![]() 的最小值。
的最小值。
(1)解:![]() =1,
=1,![]() 的实部的取值范围是
的实部的取值范围是![]()
(2)证明:略
(3)解:![]() 的最小值为1。
的最小值为1。