高三数 学 专 题 测 量
概率和随机变量
一、选择题：（4x8=32）
1．现有10张奖票，只有1张可中奖，第一人与第十人抽中奖的概率为 （ ）
(A)
(B) 
(C)
(D)
2．若“A+B”发生的概率为
，则
、
同时发生的概率为
（ ）
(A) (B)
(C)
(D)
3．在四个数字0，1，2，3中任取三个组成一个无重复数字的三位数，则得到偶数的概率为 ( )
(A) 
(B)
(C)
(D)
4．掷两颗骰子，设出现点数之和为12,11,10的概率依次为
，
，
（ ）
(A)=<
(B)<= (C)<< (D) >>
5.下面说法正确的是 （ ）
A．离散型随机变量ξ的期望Eξ反映了ξ取值的概率的平均值
B．离散型随机变量ξ的方差Dξ反映了ξ取值的平均水平
C．离散型随机变量ξ的期望Eξ反映了ξ取值的平均水平
D．离散型随机变量ξ的方差Dξ反映了ξ取值的概率的平均值
6．同时抛掷4枚均匀的硬币80次，设4枚硬币正好出现2枚正面向上，2枚反面向上的次数为ξ，则ξ的数学期望是 （ ）
A．20 B．25 C．30 D．40
7. 已知随机变量
的分布列为
|
| －1 | 0 | 1 |
| P | 0.5 | 0.3 | 0.2 |
则最可能出现的值是 (
)
A. 0.5 B. －1 C. 0 D. 1
8. 有N件产品,其中有M件次品,从中不放回地抽n 件产品,抽到的次品数的数学期望值是( )
A.
n
B. 
C. 
D. 
二、填空题(4x4=16)
9．有红、黄、篮三种颜色的旗帜各三面，在每种颜色的三面旗帜上分别标上号码
1、2和3．现任取出三面，则它们的颜色和号码均不相同的概率为 ．
10．在3次独立重复试验中，随机事件A恰好发生1次的概率不小于其恰好发生2次的概率，则A在一次试验中发生的概率P的取值范围是
11．袋中有一些大小相同的小球，其中号数为1的小球1个，号数为2的小球2个，号数为3的小球3个，……，号数为n的小球n个，从袋中取一球，其号数记为随机变量ξ，则ξ的数学期望Eξ= .
12．抛掷两个骰子，当至少有一个的点数的3的倍数时，就说这次试验成功，设在50次试验中成功的次数为，则E=
，D=
（精确到0.01）
三、 解答题(13,14,16,17每题10分;15题12分)
13．在某次考试中，甲、乙、丙三人合格（互不影响）的概率分别是
,
考试结束后，最容易出现几人合格的情况？
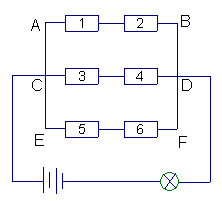
14．有如图连接的6个元件，它们断电的概率第一个为P1=0.6，第二个为P2=0.2，其余四个都为P=0.3.求电器断电的概率．
15.设一射手平均每射击10次中靶4次,求在5次射击中:(1)恰击中1次的概率;(2)第二次击中的概率;(3)恰击中2次的概率;(4)第二、三两次击中的概率;(5)至少击中1次的概率.
16．摇奖器有10个小球，其中8个小球上标有数字2，2个小球上标有数字5，现摇出3个小球，规定所得奖金（元）为这3个小球上记号之和，求此次摇奖获得奖金数额的数学期望.
17.甲、乙两名射手在一次射击中的得分是两个随机变量,分别记为和
,它们的分布列分别为
|
| ０ | １ | ２ |
| P | ０.1 | a | 0.4 |
|
| 0 | 1 | 2 |
| P | 0.2 | 0.2 | b |
(1) 求a , b 的值
(2) 计算和的期望与方差,并以此分析甲、乙两射手的技术情况.
答案：
1-8 CDAC CCBC
9-12 1/14 ,
, 
27.78,12.35
13．解：按以下四种情况计算概率,概率最大的就是最容易出现的情况.
⑴三人都合格的概率
⑵三人都不合格的概率为
⑶恰有两人合格的概率
⑷恰有一人合格的概率
由此可知，最容易出现恰有１人合格的情况
14．分别设AB、CD、EF三线路断电事件为M、N、G，每个线路断电则二个元件至少有一个断电，且它们是相互独立的，于是
=1－（1－0.6）（1－0.2）=1－0.4×0.8=0.68，
=1－（1－0.3）（1－0.3）=1－0.7×0.7=0.51．由于事件M、N、G相互独立，所以电器断电的概率
=0.68×0.51×0.51=0.177．
另解：分别设AB、CD、EF三线路断电事件为M、N、G，每个线路断电则二个元件至少有一个断电，且它们是相互独立的，于是=1－（1－0.6）（1－0.2）=1－0.4×0.8=0.68，
=1－（1－0.3）（1－0.3）=1－0.7×0.7=0.51．由于事件M、N、G相互独立，所以电器断电的概率=0.68×0.51×0.51=0.177．
15．由题设,此射手射击1次,中靶的概率为0.4,此射手射击5次,是一独立重复试验,可用公式
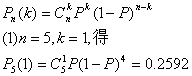
(2)事件“第二次击中”表示第一、三、四、五次击中或击不中都可,它不同于“击中一次”,也不同于“第二次击中,其他各次都不中”,不能用独立重复试验的概率公式,其实,“第二次击中”的概率,就是此射手“射击一次击中”的概率为0.4.
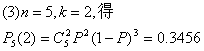
(4)“第二、三两次击中”表示第一次、第四次及第五次可中可不中,所以概率为0.4×0.4=0.16
(50设“至少击中一次”为事件B,则B包括“击中一次”,“击中两次”,“击中三次”,“击中四次”,“击中五次”,所以概率为
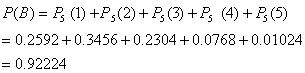事件B是用“至少”表述的,可以考虑它的对立事件.B的对立事件是“一次也没有击中”,所以B事件的概率可以这样计算:
16．设此次摇奖的奖金数额为ξ元，当摇出的3个小球均标有数字2时，ξ=6；当摇出的3
个小球中有2个标有数字2，1个标有数字5时，ξ=9；当摇出的3个小球有1个标有
数字2，2个标有数字5时，ξ=12。
所以，
Eξ=6×
（元）
答：此次摇奖获得奖金数额的数字期望是
元
17. (1) a = 0.5 b = 0.6
(2) 
=1.3 
=0.41 
= 1.4 
= 0.64
两者比较略去.