高考模拟试卷3
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1、已知f（x）=
，则f －1（
）=（ ）
（A）
（B）－1 （C）
（D）
2、一个单位职工150人，其中有业务人员110人，管理人员15人，后勤服务人员25人。为了了解职工的某种情况，要从中抽取一个容量为30的样本，则应抽取管理人员 （ ）
A、15人 B、5人 C、3人 D、2人
3、已知
，则下列不等式一定成立的是（ ）
（A）a2＞b2 （B）ln a＞ln b （C）
（D）
＞
4、如果
=a，
=b，，则a=b是四点A、B、D、C构成平行四边形的（ ）
（A）充分为必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
5、已知{
}的前n项和Sn=n2－4n+1，则a1+a2+…+a10=（ ）
（A）67 （B）65 （C）61 （D）56
6、一个凸多面体的顶点数为20，棱数为30。则它的各面多边形的内角总和为（ ）
A、2160° B、5400° C、6480° D、7200°
7、方程
=
的解集是
（ ）
（A）（－1，0）∪（3，+∞） （B）（－∞，－1）∪（0，3）
（C）（－1，0]∪[3，+∞） （D）（－∞，－1）∪[0，3]
8、曲线y=2x－x3在横坐标为－1的点处的切线为l，则点（3，2）到l的距离等于
A、
B、
C、
D、
（ ）
9、已知cos（α－β）=
，sinβ=－
，且α∈（0，
），β∈（－，0）则
sinα=（ ）
（A）
（B）
（C）－ （D）－
10、已知x、y满足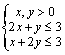
，则z=x+y的最大值为 （ ）
（A）
（B）4 （C）1 （D）2
11、等差数列{
}与{
}的前n项和分别为
与
，且
，则
=
（A）
（B）
（C）1 （D）
（ ）
12、由等式x 4+a1x3+a2x2+a3x+a4=（x+1）4+b1（x+1）3+b2（x+1）2+b3（x+1）+b4。定义映射f:（a1，a2，a3，a4）
（b1，b2，b3，b4），则f（4，3，2，1）等于（ ）
A、（1，2，3，4） B、（0，3，4，0）
C、（－1，0，2，－2） D、（0，－3，4，－1）
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
13、若球的体积是
π，则其表面积为
14、等比数列{}中，a4+a6=3，则a5（a3+2a5+a7）=
15、某物体一天中的温度T是时间t的函数，T（t）=t3－3t+60，时间单位是小时，温度单位是℃。t=0时表示12时，其后t取正值。则上午9时该物体的温度为 ℃
16、关于函数f（x）=2sin（3x－
），有下列命题：
①其最小正周期是
；②其图象可由y=2sin3x向左平移
个单位得到；
③其表达式可改写为y=2cos（3x－）；④在x∈[
，
]上为增函数。
其中正确的命题的序号是
三、解答题：本大题共6小题共74分．解答应写出文字说明．证明过程或演算步骤．
17、（本小题满分12分）
已知10件产品中有2件是次品。（1）任意取出4件产品作检验，求其中恰有1件是次品的概率。（2）为了保证使2件次品全部检验出的概率超过0.6，至少应抽取几件产品作检验？
18、（本小题满分12分）
已知向量ａ＝（x，x－4），向量ｂ＝（x2，
x），x∈[－4，2]
⑴试用x表示ａ·ｂ
⑵求ａ·ｂ的最大值，并求此时ａ、ｂ夹角的大小。
19、（本小题满分12分）
如图，直四棱柱ABCD-A1B1C1D1的底面是
梯形，AB∥CD，AD⊥DC，CD=2，DD1=AB=1，
P、Q分别是CC1、C1D1的中点。点P到直线
AD1的距离为
⑴求证：AC∥平面BPQ
⑵求二面角B-PQ-D的大小
20、（本小题满分13分）
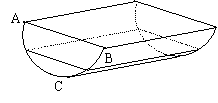如图，平地上有一条水沟，沟沿是两条长100米的平行线段，沟宽AB长2米，与沟沿垂直的平面与沟的交线是一段半圆弧，圆弧中点为C，对称轴与地面垂直，沟中水深为0.4米。
⑴求水面宽；
⑵沟中水有多少立方米？
（柱体的体积=柱体的底面积×高，
sin0.927=0.8）
⑶若要把水沟改挖（不得填土）成截面为等腰梯形的沟，使沟的底面与地面平行，改挖后的沟底宽为多少时，所挖的土最少？（结果保留根号）
21、（本小题满分12分）
已知f（x）=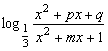
。是否存在实数p、q、m，使f（x）同时满足下列三个条件：①定义域为R的奇函数；②在[1，+∞）上是减函数；③最小值是－1。若存在，求出p、q、m；若不存在，说明理由。
22、（本小题满分13分）
已知椭圆C的方程为
（a＞b＞0），双曲线
的两条渐近线为l1、l2，过椭圆C的右焦点F作直线l，使l⊥l1，又l与l2交于P点。设l与椭圆C的两交点从左到右依次为B、A。求
的最大值及取得最大值时椭圆C的离心率e的值。
答 案
一、1、B 2、C 3、D 4、B 5、A 6、C 7、C 8、A 9、A 10、D
11、A 12、D
二、13、9π 14、9 15、42 16、①④
三、17、⑴
=
（5分）
⑵设抽取n件产品作检验，则
＞0.6， （8分）
得n（n－1）＞54
∴n≥8 即至少应抽取8件产品才能满足题意。 （12分）
18、⑴ａ·ｂ=
（3分）
⑵设f（x）=，则f '（x）=3x2+3x－6
令f '（x）=0 得x=1或－2。当x∈（－∞，－2）时，f '（x）＞0，f（x）为增函数，x∈（－2，1）时，f '（x）＜0，f（x）为减函数，x∈（1，+∞）时，f '（x）＞0，f（x）为增函数。
故f（x）极大值为f（－2）=10
又x∈[－4，2]，f（－4）=－16 f（2）=4
∴当x=－2时，ａ·ｂ的最大值为10 （9分）
此时，ａ=（－2，－6），ｂ=（4，－3），ａ=
，ｂ=5
设夹角为θ，cosθ=
=
，∴ａ、ｂ的夹角为arccos （12分）
19、⑴连接CD1 ∵P、Q分别是CC1、C1D1的
中点。∴CD1∥PQ 故CD1∥平面BPQ
又D1Q=AB=1，D1Q∥AB，
得平行四边形ABQD1，故AD1∥平面BPQ
∴平面ACD1∥平面BPQ
∴AC∥平面BPQ （4分）
⑵设DD1中点为E，连EF，则PE∥CD
∵CD⊥AD，CD⊥DD1 ∴CD⊥平面ADD1
∴PE⊥平面ADD1
过E作EF⊥AD1于F，连PF。则PF⊥AD1，PF为点P到直线AD1的距离（6分）
PF=，PE=2 ∴EF= 又D1E=，D1D=1，∴AD=1
（8分）
取CD中点G，连BG，由AB∥DG，AB=DG得GB∥AD。∵AD⊥DC，AD⊥DD1∴AD⊥平面DCC1D1，则BG⊥平面DCC1D1
过G作GH⊥PQ于H，连BH，则BH⊥PQ，故∠BHG是二面角B-PQ-D的平面角。 （10分）
由△GHQ∽△QC1P得GH=
，又BG=1，得tan∠BHG=
∴二面角B-PQ-D大小为arctan
（12分）
|
|
=OE·∠DOE=2∠EOF
扇形ODE的面积=
×1×=0.927
（5分）
△ODE的面积=×OF×DE=0.48
∴沟中水有100×（0.927－0.48）= 44.7（立方米） （7分）
S=
=
（9分）
Ssin2θ－cos2θ=2，
sin（2θ－arctan
）=2
得
≤1 ∴S≥
即S最小值为，此时sin（2θ－30°）=1
∴θ=60°，MN=2PN=2OPcot60°=
。
即改挖后的沟底宽为米
（13分）
21、∵f（x）是奇函数 ∴f（0）=0 得q=1 （1分）
又f（－x）=－f（x） ∴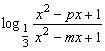
=－
=
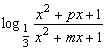
即（x2+1）2－p2x2=（x2+1）2－m2x2
∴p2=m2
若p=m，则f（x）=0，不合题意。故p=－m≠0
∴f（x）=
（5分）
由f（x）在[1，+∞）上是减函数，令g（x）=
=1－
=1－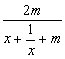
∵
在[1，+∞）上递增，在（－∞，－1]也递增，只有m＞0时，在[1，+∞）上g（x）递增，从而f（x）递减。
（7分）
∴x=－1时，在（－∞，－1]上取得最大值－2，此时由f（x）的最小值为－1得g（x）的最大值为3。
1－
=3 得m=1，
（10分）
从而p=－1
∴存在p=－1，q=1，m=1。 （12分）
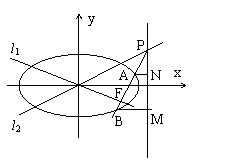22、设C的半焦距为c，l1：y=
，l2：y=
得
P（
，
），故P点在椭圆的右准线上 （2分）
设A分FP的比为λ，则A（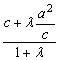
，
）
∵A在椭圆上，代入得
（c2+λa2）2+λ2a4=a2c2（1+λ）2
两边同除以a4，由
得 λ2=
（0＜e＜1）
∴λ2=－[（2－e2）+
]+3≤3－2=（－1）2
当且仅当2－e2=，即e=
时，λ最大值－1 （6分）
分别过A、B作椭圆C的右准线的垂线，垂足分别为N、M。设=t，则MB=tNA。
∵BM=
，AN=
∴BF=tAF
∴AB=BF+AF=（t+1）AF
又PB=AB+PA ∴AB=PB－PA=（t－1）PA
∴（t+1）AF=（t－1）PA 又AF=λAP
∴λ=
（11分）
∵λ≤－1 得t≤+1
的最大值为+1，此时椭圆C 的离心率e= （13分）