高考能力测试步步高数学基础训练22
基础训练22 不等式的应用
●训练指要
利用基本不等式求解最值问题及范围问题.
一、选择题
1.若函数y=lg［1＋
(1＋log2x)］的值域为(0,+∞)，则其定义域为
A.(0,+∞) B.(1，＋∞)
C.(
，＋∞) D.(，1)
2.当0≤x≤1时，x2(3－x)的最大值是
A.0 B.2 C.
D.4
3.若关于x的方程9x＋(４＋a)3x＋４＝0有解，则实数a的取值范围为
A.(－∞，－8
∪［0，＋∞
B.(－∞，－4)
C.［－8，4 D.(－∞，－8］
二、填空题
4.已知关于x的方程()x＝
有正根，则实数a的取值范围是_________.
5.若x∈［0，1］，则y=x-x3的最大值是_________.
三、解答题
6.已知关于x的方程lg(ax－2)－lg(x－2)＝1有解，求实数a的取值范围.
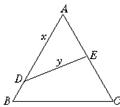
7.如图，某山区有一块边长为2a的等边△ABC实验田，DE把它分成面积相等的两部分作对比试验.
(1)设AD=x,DE=y，试求用x表示y的函数关系式；
(2)求使分界线DE为最短或最长的分法.
8.对于任意x∈R,x2-4ax+2a+30≥0(a∈R)恒成立，求关于x的方程
=a-1+1的根的范围.
高考能力测试步步高数学基础训练22答案
一、1.D 2.D 3.D
二、4.
＜a＜1
5.
三、6.1＜a＜10.
7.(1)y=
(a≤x≤2a).
(2)当x=
a时，DE取最小值a;
当x=2a时，DE取最大值
a.
8.［
,18］