高考数学创新填空题训练题
填空题一直成为高考数学改革创新的“试验田”,常出现以各类探索性试题,主要有:新定义题、新运算题、新定理题、多选题、开放题(条件、结论、综合开放题)、图表题等.下面精选29道开放探索性试题,供练习.
1.对于任意定义在R上的函数f(x),若实数x0满足f(x0)=x0,则称x0是函数f(x)的一个不动点,若函数f(x)=x2+ax+1没有不动点,则实数a的取值范围是_______.
2.设复数z=a+bi (a,b∈R),写出两个z为纯虚数的必要且不充分条件是_____或_____。
3.关于复数![]() 有下列命题。
有下列命题。
①
若![]() ;
;
②
将复数z在复平面内对应的向量![]() 逆时针旋转90°得向量
逆时针旋转90°得向量![]() ,则向量
,则向量![]() 对应的复数是:
对应的复数是:![]() ;
;
③ 复数z在复平面内对应点的轨迹是单位圆;
④
复数![]() 的辐角主值是a。
的辐角主值是a。
其中正确命题的序号是_____。
4.对于函数f(x)=2x-2-x,下列命题中,写出你认为正确的命题的所有序号_______.
① f(x)的图象关于原点对称;
② f(x)在R上是增函数;
③ f-1(2)=log23;
④ f(x)有最小值0.
5.下列命题中,写出你认为正确的命题的所有序号_______.
①![]() 是f(x)的反函数,如果它们的图象有交点,则交点必在直线y=x上;
是f(x)的反函数,如果它们的图象有交点,则交点必在直线y=x上;
②若![]() 是f(x)的反函数,那么方程f(x)=0至少有一个根;
是f(x)的反函数,那么方程f(x)=0至少有一个根;
③如果函数f(x)满足f(x-a)=f(a-x),则函数f(x)的图象关于直线x=a对称;
④函数y=f(x-a)与y=f(a-x)的图象关于直线x=a对称;
⑤若y=f(x)为单调增函数,则y=f(ax)(a>0,且a≠1)也为单调增函数.
6.定义域为R的奇函数f(x)是减函数,设a+b≤0,给出下列不等式
① f(a)·f(-a)≤0;
② f(b)·f(-b)≥0;
③ f(a)+f(b)≤f(-a)+f(-b);
④ f(a)+f(b)≥f(-a)+f(-b).
其中正确不等式的所有序号_______.
7.等差数列{an}中,Sn是它的前n项之和,且S6<S7,S7>S8,则
① 数列{an}中,前七项是递增的,从第八项开始递减;
② S9一定小于S6;
③ a1是各项中最大的;
④ S7不一定是Sn的最大值.
其中正确的命题的所有序号是_______.
8.下列命题中,写出你认为正确的命题的所有序号_______.
① 虚数的平方根仍是虚数;
② ![]() 、
、![]() ∈C且
∈C且![]() 2+
2+![]() 2=0,则
2=0,则![]() =
=![]() =0;
=0;
③ 复数k为纯虚数的充要条件是z+![]() =0;
=0;
④ z1、z2∈C,则![]() ∈R;
∈R;
⑤ ![]() 是z的一个五次方根,则
是z的一个五次方根,则![]() 也是z的五次方根;
也是z的五次方根;
⑥ 关于x的实系数二次方程ax2+bx+c=0的两个根是![]() 、
、![]() ,则
,则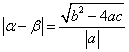 .
.
9.关于复数z=cos![]() +isin
+isin![]() ,
,![]() ∈(0,2
∈(0,2![]() ],有下列命题:
],有下列命题:
① 若z=![]() ,则
,则![]() 必是
必是![]() 的整数倍;
的整数倍;
② 将复数z在复平面内对应向量![]() 逆时针旋转90°得向量
逆时针旋转90°得向量![]() ,则
,则![]() 对应的复数是-sin
对应的复数是-sin![]() +icos
+icos![]() ,
,![]() ∈(0,2
∈(0,2![]() ];
];
③ 复数z在复平面内对应点的轨迹是单位圆;
④ 复数z2的辐角主值是![]() .
.
其中错误命题的所有序号是_______.
10.下列命题中,写出你认为正确的命题的所有序号_______.
① 存在实数![]() ,使得sin
,使得sin![]() cos
cos![]() =1成立;
=1成立;
② 存在实数![]() ,使得sin
,使得sin![]() +cos
+cos![]() =
=![]() 成立;
成立;
③ y=![]() 是偶函数;
是偶函数;
④ x=![]() 是函数y=
是函数y=![]() 的图象的一条对称轴方程;
的图象的一条对称轴方程;
⑤ 若![]() 、
、![]() 是第一象限,且
是第一象限,且![]() >
>![]() ,则tan
,则tan![]() >tan
>tan![]() .
.
11.下列命题中,写出你认为正确的命题的所有序号_______.
① 若2![]() +
+![]() =
=![]() ,则y=cos
,则y=cos![]() -6sin
-6sin![]() 有最大值为7,最小值为-5;
有最大值为7,最小值为-5;
② 函数y=2sin2x的图象沿x轴向左平移![]() 个单位(0<
个单位(0<![]() <
<![]() )后图象的一个对称中心为(
)后图象的一个对称中心为(![]() ,0),则
,0),则![]() 的值为
的值为![]() ;
;
③ 函数y=arc cosx-![]() 是奇函数且增函数;
是奇函数且增函数;
④ 对于函数f(x)=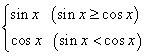 ,当且仅当x=2k
,当且仅当x=2k![]() +
+![]() (k∈Z)时取最大值1.
(k∈Z)时取最大值1.
12.下列命题中,写出你认为正确的命题的所有序号_______.
① 函数y=-4sin(-![]() x+
x+![]() )的相位是-
)的相位是-![]() x+
x+![]() ,初相是
,初相是![]() ;
;
② 若sinx+siny=![]() ,则siny-cos2x的最大值是
,则siny-cos2x的最大值是![]() ;
;
③ 函数y=sin(![]() -2x)的单调增区间是[k
-2x)的单调增区间是[k![]() -
-![]() ,k
,k![]() +
+![]() ](k∈Z);
](k∈Z);
④ 函数f(x)=![]() 是奇函数;
是奇函数;
⑤ 函数f(x)=tan![]() -
-![]() 的最小正周期是
的最小正周期是![]() ;
;
⑥ 设![]() 是第二象限,则tan
是第二象限,则tan![]() >cot
>cot![]() ,且sin
,且sin![]() >cos
>cos![]() .
.
13.下列命题中,写出你认为错误的命题的所有序号_______.
① 在ΔABC中,已知sinA=![]() ,cosB=
,cosB=![]() ,则cosC=
,则cosC=![]() ;
;
② 函数y=3sin(2x+![]() )的图象可看作把y=3sin2x的图象向左平移
)的图象可看作把y=3sin2x的图象向左平移![]() 个单位而得到;
个单位而得到;
③ 在ΔABC中,A>B是sinA>sinB的充要条件;
④ 函数f(x)=![]() 的最小正周期是
的最小正周期是![]() .
.
14.已知m、n是不重合的两条直线,![]() 、
、![]() 、
、![]() 是不重合的三个平面,下列命题中,写出你认为正确的命题的所有序号_______.
是不重合的三个平面,下列命题中,写出你认为正确的命题的所有序号_______.
①若![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,则
,则![]() ∥
∥![]() ;
;
②若n⊥![]() ,n⊥
,n⊥![]() ,则
,则![]() ∥
∥![]() ;
;
③若![]() 内有不共线的三点到
内有不共线的三点到![]() 的距离相
的距离相![]() 等,则
等,则![]() ∥
∥![]() ;
;
④若n、m在![]() 内,且n∥
内,且n∥![]() ,m∥
,m∥![]() ,则
,则![]() ∥
∥![]() ;
;
⑤ 若n、m为异面直线,且n![]()
![]() ,n∥
,n∥![]() ,m
,m![]()
![]() ,n∥
,n∥![]() ,则
,则![]() ∥
∥![]() .
.
15.在空间,下列命题中,写出你认为正确的命题的所有序号______.
①a、b是异面直线,过a有且只有一个平面与b平行;
②a、b是异面直线,过a有且只有一个平面与b垂直;
③a是平面![]() 的一条斜线,过a有且只有一个平面与
的一条斜线,过a有且只有一个平面与![]() 垂直;
垂直;
④a是平面![]() 个的一条直线,过a有且只有一个平面与
个的一条直线,过a有且只有一个平面与![]() 平行.
平行.
16.设a、b、c表示不重合的三条直线,![]() 、
、![]() 、
、![]() 表示不重合的三个平面,下列命题中,写出你认为正确的命题的所有序号_______.
表示不重合的三个平面,下列命题中,写出你认为正确的命题的所有序号_______.
①若a∥c,b∥c,则a∥b;
②若a∥![]() ,b∥
,b∥![]() ,则a∥b;
,则a∥b;
③![]() ∥
∥![]() ∥
∥![]() ,a与
,a与![]() ,b与
,b与![]() ,c与
,c与![]() 所成的角相等,则a∥b∥c;
所成的角相等,则a∥b∥c;
④![]() ∥c,
∥c,![]() ∥c,则
∥c,则![]() ∥
∥![]() ;
;
⑤![]() ∩
∩![]() =c,
=c,![]() ∩
∩![]() =a,
=a,![]() ∩
∩![]() =b,若a∩b=
=b,若a∩b=![]() ,则a∥b∥c.
,则a∥b∥c.
17.下列命题中,写出你认为正确的命题的所有序号_______.
①侧棱长均相等的棱锥的顶点在底面内的射影为底面多边形外接圆的圆心;
②在正棱锥中,若侧面与底面所成的角为![]() ,记侧面面积为S1,底面积为S2,则S2=S1cos
,记侧面面积为S1,底面积为S2,则S2=S1cos![]() ;
;
③四面体侧面的四个三角形中,直角三角形最多有三个;
④平面![]() 截正方体ABCD—A1B1C1D1,与AB、AD、AA1分别交于P、Q、R,则截面ΔPQR一定是锐角三角形;
截正方体ABCD—A1B1C1D1,与AB、AD、AA1分别交于P、Q、R,则截面ΔPQR一定是锐角三角形;
⑤圆锥过两条母线的截面中,以轴截面的面积为最大.
18.三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为凹数,如524、746等都是凹数.那么,各个数位上无重复数字的三位凹数共有 个.
19.用![]() 克的某种溶质配制成一定浓度的
克的某种溶质配制成一定浓度的![]() 克溶液
克溶液![]() 。若将其溶质减少
。若将其溶质减少![]() 克
克![]() ,会使溶液的浓度降低;而将其溶质增加
,会使溶液的浓度降低;而将其溶质增加![]() 克,会使溶液的浓度增大。请根据这一现象提炼出一个不等式:
克,会使溶液的浓度增大。请根据这一现象提炼出一个不等式:
20.若对n个复数![]() 1,
1,![]() 2,…,
2,…,![]() n,存在n个不全为零的实数k1,k2,…,kn使得k1
n,存在n个不全为零的实数k1,k2,…,kn使得k1![]() 1+k2
1+k2![]() 2+…+kn
2+…+kn![]() n=0成立,则称
n=0成立,则称![]() 1,
1,![]() 2,…,
2,…,![]() n为“线性相关”.依此规定,能使
n为“线性相关”.依此规定,能使![]() 1=1,
1=1,![]() 2=1-i,
2=1-i,![]() 3=2+2i“线性相关”的实数k1,k2,k3依次可以取 .(写出一组数值即可,不必考虑所有情况)
3=2+2i“线性相关”的实数k1,k2,k3依次可以取 .(写出一组数值即可,不必考虑所有情况)
21.电子计算机中使用二进制,它与十进制的换算关系如下表示:
| 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 二进制 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | … |
观察二进制为1位数、2位数、3位数时,对应的十进制的数,当二进制为6位数时,能表示十进制中的最大数是 。
22.已知二次函数y=f(x)在[-1,2]上存在反函数,请你写出满足此条件的f(x)的一个解析式:f(x)=_______.
23.对于平面几何中的命题:“如果两个角的两边分别对应垂直,那么这两个角相等或互补.”在立体几何中,类比上述命题,可以得到命题:“ .”这个类比的命题的真假性是 .
24.已知α、β是两个平面,直线a不在平面α内,设①a⊥α,②a∥β,③α⊥β,若取①、②、③中的两个为条件,另一个为结论构造三个命题,写出一个正确的命题是: .
25.设U={1,2,…,9},A与B是U的子集,若A∩B={1,2,3},就称集对(A,B)为“好集”,那么所有好集的个数是_______.
26.对于实数x,y,新运算x※y=ax+by+c,其中a,b,c是常数,等式右边是通常的加法和乘法运算.若3※5=15,4※7=28,则 1※1=_______.
27.对于实数x,若n≤x<n+1(n∈N),规定[x]=n,则不等式4[x]2-36[x]+45<0的解集是_______.
28.在正实数集上定义一个新运算※,其规则为:当a≥b时,a※b=b3;当a<b时,a※b=b2.根据这个规则,方程3※x=27的解是_______.
29.对于顶点在原点的抛物线,给出下列条件:
①焦点在![]() 轴上;②焦点在
轴上;②焦点在![]() 轴上;
轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的通径的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为![]() 。
。
能使这抛物线方程为![]() 的条件是 (要求填写合适条件的序号).
的条件是 (要求填写合适条件的序号).
练习答案
1. (-1,3)
2.a=0或z+![]() =0 .
=0 .
3.①②.
4.①②④
5.④
6.①④
7.②③
8.①④⑤
9.③④
10. ③④
11.①②
12.⑤
13.①②④
14.②⑤
15.①③
16.①⑤
17.③⑤
18.240
19.![]()
20.-4,2,1等等.
21.![]() .
.
22.答案不唯一,只要写一个正确的即可。例:f(x)=(x+1)2
23.答案多种,如①如果一个角的两边与一个二面角的两个半平面分别对应垂直,那么这个角与二面角的平面角相等或互补,这个命题是正确的;②如果两个二面角的两个半平面分别对应垂直,那么这两个二面角的平面相等或互补,这个命题是错误的。
24.![]()
25. 36个.
解析
令A1=A-{1,2,3},B1=B-{1,2,3},则A1∩B1=![]() ,且(A1,B1)与(A,B)一一对应,A1,B1
,且(A1,B1)与(A,B)一一对应,A1,B1![]() {4,5,6,7,8,9}.
{4,5,6,7,8,9}.
又所有(A1,B1)的个数为![]() =(1+2)6=36.
=(1+2)6=36.
26.-11.
解析 依题设,有
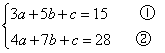 ,①×3-②×2,得a+b+c=-11.
,①×3-②×2,得a+b+c=-11.
故1※1=a+b+c=-11.
27.{ x│2≤x<8 }.
解析 由题意得,![]() ,再由新定义知2≤[x]≤7,故原不等式的解集是{ x│2≤x<8 }.
,再由新定义知2≤[x]≤7,故原不等式的解集是{ x│2≤x<8 }.
28.3或3![]() .
.
解析 当3≥x时,3※x=x3;当3<x时,3※x=x2.于是原题可转化为两个常规方程
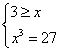 或
或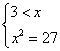 ,解得x=3或x=3.
,解得x=3或x=3.
29.②、⑤