高三数学月考试卷
班级 姓名 考试号
一：选择题（共计60分，每小题5分）
1．若U是全集，A是U的一个真子集，则下列结论中错误的是 【 】
A． U∩A=A B．U∪A=U C．CUA∪A=U D．CUA∩A≠Φ
２．下列命题中，使命题M是命题N成立的充要条件的一组命题是 【 】
A．M：a>b; N：ac2>bc2 B．M：a>b,c>d, N：a－d >b－c
C．M：a>b>0,c>d>0, N：ac>bd D．M：a－b=a+b, N：ab≤0
3．已知
在区间（4，
）上是增函数，则a的范围是【 】
A．a≤－２ Ｂ.a≥－2 C.a≥－6 D. a≤－6
4．设角α满足条件sin2α＜0，cosα－sinα＜0，则角α在 【 】
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．已知sin（x+y）cosx－cos（x+y）sinx = 
，
，则tan2y的值是 【 】
A．
B．
C．
D．
6．函数
的最大值为 【 】
A．10 B．9 C．8 D．7
7．已知等差数列
满足
则有
【 】
A．
B．
C．
D．
8．首项为31，公差为－6的等差数列
中，前n项的和为Sn，则数列
中与零最近的项是 【 】
A．第9项 B．第10项 C．第11项 D．第12项
9．函数
的反函数的图象经过点（4，2），则
的值是 【 】 A．－
B．
C．2 D．4
10．已知
是定义在R上的偶函数，且
在（0，+∞）上是减函数，如果
，
且
则有 【 】
A．
B．
C．
D．
11．函数
的值域是 【 】 A．（－∞，0） B．[－3，0] C．
D．
12．已知f (x)定义在R上的奇函数，当x<0时
，那么
的值是 【 】
A．9 B．
C．
D．
二：填空题（共计16分，每小题4分）
13．已知点（1，2）既在函数
的图象上，又在它的反函数图象上，则a=
b=
.
14．已知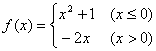
，若f(x)=10,则x=
。
15．已知
=
.
16．已知奇函数f(x)在定义域 [－a,a](a>0)上是增函数，且 f(a)=1, 其反函数为
则函数
的定义域为
三：解答题（共计74分）
１7：已知等比数列{an}及等差数列{bn}其中b1=0，公差d≠0，将这两个数列对应项相加得一新数列1，1，2，……求这个新数列前10项之和。（本题11分）
18．已知
的值.
（本题12分）
19．有两个命题：M：关于x的方程4x2－4kx+k+2＝0有实数根；命题N：关于x的不等式2－x+x－1>k－2的解集为R。若复合命题“M或N”为真，“M且N”为假，求实数k的取值范围。（本题12分）
20．已知函数f(x)=ax2－2x＋1（a>0）.
（1）求 f(x)在区间[1，3]上的最小值；
（2）令g（x）=
当a=1时，试判定函数g（x）在区间（1，+∞）上的单调性. （本题13分）
21．：设数列{an}是以a为首项，t为公比的等比数列，令bn=1+a1+a2+…+an,
cn=2+ b1+b2+…+bn,n∈N*.
（Ⅰ）试用a, t表示bn和cn;
（Ⅱ）若a>0,t>0且t≠1，试比较cn与cn+1（n∈N*）的大小；
（Ⅲ）是否存在实数对（a, t），其中t≠1，使{cn}成等比数列，若存在，求出实数对（a,t）和{cn},若不存在说明理由. （本题13分）
22．已知二次函数
满足
，对于任意x都有
并且当
时，有
．
(1) 求f (1)的值；
(2) 证明a>0，c>0；
(3) 当
时，函数
是单调的，
求证：m≤0，或m≥1．（本题13分）
参考答案：
一：选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | D | B | B | B | D | C | C | B | C | D | D |
二：填空题
13．a＝－3，b＝7 14.－3 15。 －3 16。[
，
]
三：解答题
17．【解】：设等比数列首项为a,公比为q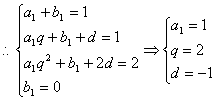
……6分
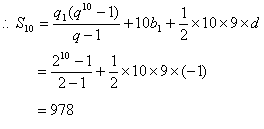……………………………11分
18．【解】：
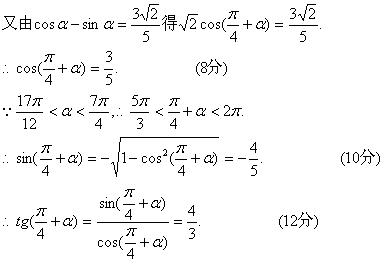
19．【解】：由关于x的方程4x2－4kx+k+2＝0有实数根得：
△＝(－4k)2－16(k+2)≥0, k≥2或者k≤-1.………………………2分
由关于x的不等式2－x+x－1>k－2的解集为R得k－2<1 ,k<3………5分
因为：复合命题“M或N”为真，“M且N”为假
（1）M为假，N为真时，
－1<k<2………………8分
(2) M为真，N为假时，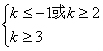
k≥3…………11分
综上得：实数k的取值范围是－1<k<2或k≥3………………………12分
20．【解】：（1）
……2分
∵>0∴抛物线开口向上.
当
<1，即a>1时，f(x)在[1，3]上单调递增，最小值为f(1)=a－1;
当1≤≤3，即
时，最小值为f（）=1－；……6分
当3,即0<a<
时，
在[1，3]上单调递减，最小值为f(3)=9a－5 .……8分
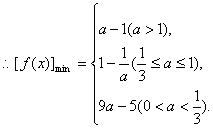……9分
（2）当a=1时，
…………………………10分
任取1<x1<x2 ,
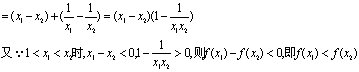
∴f(x)在（1，+∞）上为增函数.…………………………………………………………13分
21．【解】：Ⅰ）
…2分
当
……4分
（Ⅱ）
……5分
当
所以cn+1—cn>0 ……6分
同理当0<t<1时，1―t>0,1―tn+1>0,又a>0,
所以
……7分
综上所述cn+1>cn. ……8分
（Ⅲ）若
成等比数列，
|
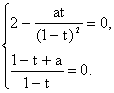……………………………10分由（2）得a=t－1,将
…………13分
所以存在实数对（a，t）为（1，2），使{cn}成为以4为首项，2为公比的等比数列.
22．【解】：(1) f(1)=1
(2)
a＝c＝
b= f(x)＝x2+x+
(3). m≤0，或m≥1