高三数学质量检测1
数 学
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共150分,考试时间120分钟。
第I卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率
P![]() (k)=C
(k)=C![]() P
P![]() (1-P)
(1-P)![]()
正棱锥、圆锥的侧面积公式S![]() =
=![]() cl 其中c表示底面周长,l 表示斜高或母线长
cl 其中c表示底面周长,l 表示斜高或母线长
球的体积公式V![]() =
=![]() 其中R表示球的半径
其中R表示球的半径
一、 选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题
目要求的。
1.已知集合M={xx-a=0},N={xax-1=0},若M![]() N=N,则实数a的值是
N=N,则实数a的值是
A.1 B.-1 C.1或-1 D.0或1或-1
2.若椭圆![]() +
+![]() =1过点(-2,
=1过点(-2,![]() ),则其焦距为
),则其焦距为
A.2![]() B.2
B.2![]() C.4
C.4![]() D.4
D.4![]()
3.已知直线l![]() :A
:A![]() x+B
x+B![]() y+C
y+C![]() =0,l
=0,l![]() :A
:A![]() x+B
x+B![]() y+C
y+C![]() =0,则
=0,则![]() =-1是l
=-1是l![]()
![]() l
l![]() 的
的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.
两非零复数z![]() 、z
、z![]() 分别对应向量
分别对应向量![]() 、
、![]() ,若 z
,若 z![]() +z
+z![]() = z
= z![]() -z
-z![]() ,则向量
,则向量![]() 与
与![]()
的关系
A.![]() =
=![]() B.
B.![]() =
=![]()
C.![]()
![]()
![]() D.
D.![]() 与
与![]() 共线
共线
5.用1,2,2,3,3,3这六个数字组成的不同六位数共有
A.20个 B.60个 C.90个 D.120个
6.若log![]() (a
(a![]() +1)<log
+1)<log![]() 2a<0,则a的取值范围是
2a<0,则a的取值范围是
A.0<a<1 B.0<a<![]() C.
C.![]() <a<1 D.a>0且a
<a<1 D.a>0且a![]() 1
1
7.已知函数y=f(x)对任意实数都有f(-x)= f(x),f(x)= -f(x+1)且在[0,1]上单调递减,则
A.f(![]() )< f(
)< f(![]() )< f(
)< f(![]() ) B.f(
) B.f(![]() )<f(
)<f(![]() )<f(
)<f(![]() )
)
C.f(![]() )<f(
)<f(![]() )<f(
)<f(![]() ) D.f(
) D.f(![]() )< f(
)< f(![]() )< f(
)< f(![]() )
)
8.把函数y=cos x的图象上的所有点的横坐标缩小到原来的一半,纵坐标扩大到原来的两倍,然后把图象向左平移![]() 个单位,则所得图形表示的函数的解析式为
个单位,则所得图形表示的函数的解析式为
A.y=2sin 2x B.y=-2sin 2x C.y=2cos(x+![]() )
D.y=2cos(
)
D.y=2cos(![]() +
+![]() )
)
9.若曲线f(x)=x![]() -x在点P处的切线平行于直线3x-y=0,则点P的坐标为
-x在点P处的切线平行于直线3x-y=0,则点P的坐标为
A.(1,3) B.(-1,3) C.(1,0) D.(-1,0)
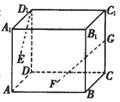 10.如图正方体ABCD—A
10.如图正方体ABCD—A![]() B
B![]() C
C![]() D
D![]() 中,E、F分别是正方形ADD
中,E、F分别是正方形ADD![]() A
A![]() 和ABCD的中心,G是CC
和ABCD的中心,G是CC![]() 的中点,
的中点,
设GF、C![]() E与AB所成的角分别为
E与AB所成的角分别为![]() 、
、![]() ,则
,则![]() +
+![]() 等于
等于
A.120° B.90° C.75° D.60°
11.若集合A![]() 、A
、A![]() 满足A
满足A![]()
![]() A
A![]() =A,则称(A
=A,则称(A![]() ,A
,A![]() )为集合A的一个分拆,并规定:当且仅当A
)为集合A的一个分拆,并规定:当且仅当A![]() =A
=A![]()
时,(A![]() 、A
、A![]() )与(A
)与(A![]() 、A
、A![]() )为集合A的同一种分拆,则集合A={a
)为集合A的同一种分拆,则集合A={a![]() ,a
,a![]() ,a
,a![]() }的不同分拆种数是
}的不同分拆种数是
A.27 B.26 C.9 D.8
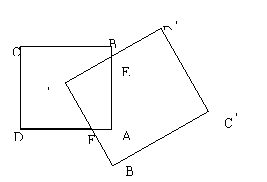 12.如图所示,正方形ABCD的中心是A
12.如图所示,正方形ABCD的中心是A![]() ,A
,A![]() B
B![]() C
C![]() D
D![]() 也是正方形,若正方形ABCD的面积是1,且A
也是正方形,若正方形ABCD的面积是1,且A![]() B
B![]() >
>![]() AB,AE>BE,两正方形的公共部分四边形AEA
AB,AE>BE,两正方形的公共部分四边形AEA![]() F的面积为S,则
F的面积为S,则
A.S=![]() B.S>
B.S>![]()
C.S<![]() D.S的大小由正方形A
D.S的大小由正方形A![]() B
B![]() C
C![]() D
D![]() 的大小与AE的大小而定
的大小与AE的大小而定
第I卷(选择题 共90分)
二、 填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13.复数![]() 满足i-
满足i-![]() =1,arg(1-
=1,arg(1-![]() )=
)=![]() ,则
,则![]() 的值
。
的值
。
14.若对n个向量a![]() ,a
,a![]() ,…,a
,…,a![]() 存在n个不全为零的实数k
存在n个不全为零的实数k![]() ,k
,k![]() ,…,k
,…,k![]() ,使得k
,使得k![]() a
a![]() + k
+ k![]() a
a![]() +…+
+…+
k![]() a
a![]() =0成立,则称向量a
=0成立,则称向量a![]() ,a
,a![]() ,…,a
,…,a![]() 为“线性相关”。依此规定,能说明a
为“线性相关”。依此规定,能说明a![]() =(1,0),a
=(1,0),a![]() =(1,-1),a
=(1,-1),a![]() =(2,2)“线性相关”的实数k
=(2,2)“线性相关”的实数k![]() ,k
,k![]() ,k
,k![]() 依次可以取 (写出一组数值即可,不必考虑所有情况)。
依次可以取 (写出一组数值即可,不必考虑所有情况)。
15.对于实数x、y,定义新运算x![]() y=ax+by+1,其中a、b是常数,等式右边是通常的加法和乘法运算,若3
y=ax+by+1,其中a、b是常数,等式右边是通常的加法和乘法运算,若3![]() 5=15,4
5=15,4![]() 7=28,则1
7=28,则1![]() 1=
。
1=
。
16.设![]() 、
、![]() 表示平面,l表示不在
表示平面,l表示不在![]() 内也不在
内也不在![]() 内的直线,存在下列三个事实,①l
内的直线,存在下列三个事实,①l![]()
![]() ,②l//
,②l//![]() ,③
,③![]()
![]()
![]() ,若以其中两个作为条件,别一个作为结论,可构成三个命题,其中真命题是 。(要求写出所有真命题)
,若以其中两个作为条件,别一个作为结论,可构成三个命题,其中真命题是 。(要求写出所有真命题)
三、 解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)
一个口袋中装有大小相同的2个白球和3个黑球。
(1) 从中摸出两个球,求两球恰好颜色不同的概率;
(2) 从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率。
18.(本小题满分12分)
数列{a![]() }中,a
}中,a![]() =1,n
=1,n![]() 2时,其前n项的和S
2时,其前n项的和S![]() 满足S
满足S![]()
![]() = a
= a![]() (S
(S![]() -
-![]() )
)
(1)
求S![]() 的表达式;
的表达式;
(2)
|
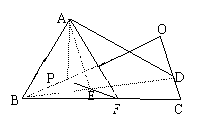
19.(本小题满分12分)
在Rt![]() ABC中,
ABC中,![]() ACB=30
ACB=30![]() ,
,![]() B=90
B=90![]() ,D为AC中点,E为BD的中点,AE的延长线交BC于F,
,D为AC中点,E为BD的中点,AE的延长线交BC于F,
将![]() ABD沿BD折起,二面角A-BD-C大小记为
ABD沿BD折起,二面角A-BD-C大小记为![]() 。
。
 |
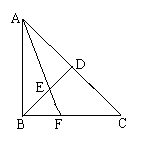
(1)
求证:面AEF![]() 面BCD;
面BCD;
(2)
![]() 为何值时,AB
为何值时,AB![]() CD。
CD。
20.(本小题满分12分)
在中国轻纺市场,当季节即将来临时,季节性服装价格呈上升趋势,设某服装开始时定价为10元,
并且每周(七天)涨价2元,5周后保持20元的价格平稳销售,10周后当季节即将过去时,平均每
周削价2元,直到16周末,该服装已不再销售。
(1) 试建立价格P与周次t的函数关系;
(2)
若此服装每件进价Q与周次t之间的关系Q=-0.125(t-8)![]() +12,t∈[0,16],t∈N。试问该服装第几周每件销售利润L最大?
+12,t∈[0,16],t∈N。试问该服装第几周每件销售利润L最大?
21.(本小题满分12分)
设双曲线C的中心在原点,以抛物线y![]() =2
=2![]() x-4的顶点为双曲线的右焦点,抛物线的准线为双曲
x-4的顶点为双曲线的右焦点,抛物线的准线为双曲
线的右准线。
(1) 试求双曲线C的方程;
(2) 设直线l:y=2x+1与双曲线C交于A、B两点,求AB;
(3) 对于直线y=kx+1,是否存在这样的实数k,使直线l与双曲线C的交点A、B关于直线y=ax(a为常数)对称,若存在,求出k的值;若不存在,请说明理由。
22.(本小题满分14分)
对于函数y=f(x),若存在实数x![]() ,满足f(x
,满足f(x![]() )= x
)= x![]() ,则称x
,则称x![]() 为f(x)的不动点,已知F
为f(x)的不动点,已知F![]() (x)=
(x)=
f(x),F![]() =f [F
=f [F![]() (x)],F
(x)],F![]() (x)=f [F
(x)=f [F![]() (x)],…,F
(x)],…,F![]() (x)=f [F
(x)=f [F![]() (x)](n
(x)](n![]() N
N![]() n
n![]() 2)。
2)。
(1)
若f(x)存在不动点,试问F![]() (x),F
(x),F![]() (x),…,F
(x),…,F![]() (x)是否也存在不动点?写出你的结论并加以证明:
(x)是否也存在不动点?写出你的结论并加以证明:
(2)
设f(x)=2x-x![]() ,求使所有F
,求使所有F![]() (x)<0(n
(x)<0(n![]() N
N![]() n
n![]() 2)成立的所有正实数x值的集合。
2)成立的所有正实数x值的集合。
高三质量检测答案
1.D a=0时,N为空集。
2.D
3.A A![]() =0,B
=0,B![]() =0时,l
=0时,l![]() 与l
与l![]() 垂直。
垂直。
4.C 对角线相等的四边形为矩形。
5.B 6!/(2!3!)
6.C 直接解不等式或者特殊值法。
7.B f(x)为以2为周期的偶函数,图象法。
8.B
9.C f![]() (x)=3
(x)=3
10.B
11.A 1C![]() +2C
+2C![]() +2
+2![]() C
C![]() +2
+2![]() C
C![]()
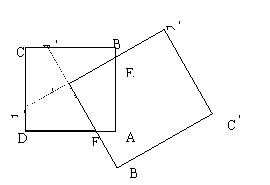 12.A 如图,延长D
12.A 如图,延长D![]() A
A![]() 交CD于E
交CD于E![]() ,延长B
,延长B![]() A
A![]() 交BC于F
交BC于F![]() ,则根据对称性,正方形被分成四个全等的四边形。
,则根据对称性,正方形被分成四个全等的四边形。
13.1+i
14.只要写出-4c,2c,c中一组即可,如-4,2,1等。
15.-11
16.①②![]() ③,①③
③,①③![]() ②
②
17.(1)记“摸出两个球,两球恰好颜色不同”为A,摸出两个球共有方法C![]() =10种,其中,两球一白一黑有C
=10种,其中,两球一白一黑有C![]() ·C
·C![]() =6种,
=6种,
![]() P(A)=
P(A)=![]() =
=![]()
(2)记摸出一球,放回后再摸出一个球“两球恰好颜色不同”为B,摸出一球得白球的概率为![]() =0.4,
=0.4,
摸出一球得黑球的概率为![]() =0.6,
=0.6,
“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,![]() P(B)=0.4×0.6+0.6×0.4=0.48
P(B)=0.4×0.6+0.6×0.4=0.48
18.(1)n![]() 2,S
2,S![]()
![]() =(S
=(S![]() -S
-S![]() )(S
)(S![]() -
-![]() )
)
![]() S
S![]() =-
=-![]()
即![]() =2(n
=2(n![]() 2)
2)
![]()
![]() =2n-1
=2n-1 ![]() S
S![]() =
=![]()
(2)b![]() =
=![]()
T![]() =
=![]() …+
…+![]() =
=![]()
![]() lim T
lim T![]() =
=![]()
19.(1)证明:在Rt![]() ABC中,
ABC中,![]() C=30
C=30![]() ,D为AC的中点,则
,D为AC的中点,则![]() ABD是等边三角形又因E是BD的中
ABD是等边三角形又因E是BD的中
点,![]() BD
BD![]() AE,BD
AE,BD![]() EF,折起后,AE
EF,折起后,AE![]() EF=E,
EF=E,![]() BD
BD![]() 面AEF
面AEF ![]() BD
BD![]() 面BCD,
面BCD,![]() 面AEF
面AEF![]() 面BCD。
面BCD。
(2)过A作AP![]() 面BCD于P,则P在FE的延长线上,设BP与CD相交于Q,令AB=1,则
面BCD于P,则P在FE的延长线上,设BP与CD相交于Q,令AB=1,则![]() ABD
ABD
是边长为1的等边三角形,若AB![]() CD,则BQ
CD,则BQ![]() CD
CD![]() PE=
PE=![]() AE=
AE=![]() 又AE=
又AE=![]()
![]() 折后有cosAEP=
折后有cosAEP=![]() =
=![]()
由于![]() AEF=
AEF=![]() 就是二面角A-BD-C的平面角,
就是二面角A-BD-C的平面角,
|
|
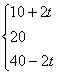 P-Q=
P-Q=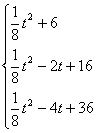
(2)t=5时,L![]() =9
=9![]() ,即第五周销售利润最大。
,即第五周销售利润最大。
21.(1)由抛物线y![]() =2
=2![]() x-4,即y
x-4,即y![]() =2
=2![]() (x-
(x-![]() ),可知抛物线顶点为(
),可知抛物线顶点为(![]() ,0),准线方程为
,0),准线方程为
x=![]() 。
。
在双曲线C中,中心在原点,右焦点(![]() ,0),右准线x=
,0),右准线x=![]() ,
,
![]()
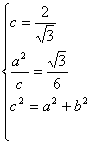
![]()
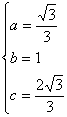
![]() 双曲线C的方程3x
双曲线C的方程3x![]() -y
-y![]() =1
=1
(2)由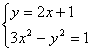
![]() 3x
3x![]() -(2x+1)
-(2x+1)![]() =1
=1![]() x
x![]() +4x+2=0
+4x+2=0
![]() AB=2
AB=2![]()
(3)假设存在实数k,使A、B关于直线y = ax对称,设A(x![]() ,y
,y![]() )、B(x
)、B(x![]() ,y
,y![]() ),则
),则
|
|
|
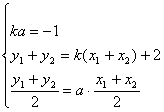
|
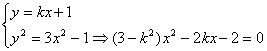
|
由④知:x![]() +x
+x![]() =
=![]() 代入⑤
代入⑤
整理得ak=3与①矛盾,故不存在实数k,使A、B关于直线y = ax对称。
22.(1)y=f(x)存在不动点x![]() ,则f(x
,则f(x![]() )= x
)= x![]() ,下证x
,下证x![]() 是F
是F![]() (x)的不动点
(x)的不动点
![]() F
F![]() (x
(x![]() )=f [ F
)=f [ F![]() (x
(x![]() )]=f [ f(x
)]=f [ f(x![]() )]= f(x
)]= f(x![]() )= x
)= x![]()
![]() x
x![]() 也是F
也是F![]() (x)的不动点
(x)的不动点
若F![]() (x)存在不动点x
(x)存在不动点x![]() ,即F
,即F![]() (x
(x![]() )= x
)= x![]()
![]() F
F![]() (x
(x![]() )=f [ F
)=f [ F![]() (x
(x![]() )]= f(x
)]= f(x![]() )= x
)= x![]()
即F![]() (x)也存在不动点x
(x)也存在不动点x![]()
综上,由数学归纳法知F![]() (x)(n
(x)(n![]() N
N![]() n
n![]() 2)都存在不动点,并且有相同的不动点
2)都存在不动点,并且有相同的不动点
(2)解不等式f(x)<0,即2x-x![]() <0
<0
得x>2或x<0
要使F![]() (x)<0(n
(x)<0(n![]() 2),即f [ F
2),即f [ F![]() (x)]<0,即2 F
(x)]<0,即2 F![]() (x)-[ F
(x)-[ F![]() (x)]
(x)]![]() <0
<0
得F![]() (x)<0或F
(x)<0或F![]() (x)>2
(x)>2
依类推,要使F![]() (x)<0,即f [ F
(x)<0,即f [ F![]() (x)]<0,即f [ f(x)]<0
(x)]<0,即f [ f(x)]<0
即2f(x)-[ f(x)]![]() <0,得f(x)<0或f(x)>2
<0,得f(x)<0或f(x)>2
由2x-x![]() <0得,x>2或x<0(舍去,x为正实数)
<0得,x>2或x<0(舍去,x为正实数)
由2x-x![]() >2得
>2得![]()
![]() 所求x的取值集合为(2,+
所求x的取值集合为(2,+![]() )
)
另解:显然,f(x)<0的解集为(-![]() ,0)
,0)![]() (2,+
(2,+![]() )
)
x=0,x=1,是y=f(x)的两个不动点,对于x<0,由数学归纳法不难得出F![]() (x)<0
(x)<0
对于x>2有F![]() (x)<0 又
(x)<0 又![]() x
x![]() (0,1)时f(x)
(0,1)时f(x)![]() (0,1),
(0,1),
![]() F
F![]() (x)= f [ f(x)]
(x)= f [ f(x)] ![]() (0,1)
(0,1)
由数学归纳法不难得出:F![]() (x)
(x)![]() (0,1),当x
(0,1),当x![]() (1,2)时,f(x)
(1,2)时,f(x)![]() (0,1)
(0,1)
从而也可得出F![]() (x)
(x)![]() (0,1),而F
(0,1),而F![]() (0)=0,F
(0)=0,F![]() (1)=1,F
(1)=1,F![]() (2)=2
(2)=2
![]() F
F![]() (x)<0成立的所有正实数x值的集合为(2,+
(x)<0成立的所有正实数x值的集合为(2,+![]() )
)