高三数学专题(平面向量)复习
班级 姓名
一、选择题
1、下列各式中正确的是 【 】
（1）(λ·a)·b=λ·(a b)=a·(λb), （2）a·b=a·b,
（3）(a·b)·c=a·(b·c), （4）(a+b)·c= a·c+b·c
A．（1）（3） B．（2）（4） C．（1）（4） D．以上都不对.
2、已知a=(2,3)，b=(－4,7)，则a在b上的投影值为 【 】
A．
B．
C．
D．
3、若向量a=(1,－2)，b=4a,且a,b共线,则b可能是 【 】
A．(4,8) B．(－4,8) C．(－4,－8) D．(8,4)
4．己知
的夹角为
,则以
为邻边的平行四边形的对角线长为 【 】
A．15
B．
C．14
D．16
5．己知P1(2,－1)、P2(0,5)且点P在P1P2的延长线上,
,则P点坐标为
【 】
A．(－2,11) B．(
C．(
,3) D．(2,－7)
6．已知：
且
∥
,
⊥
,则点C的坐标为A．(－3,－
) B．(－3,)C． (3, ) D．(3,－)【 】
7.已知向量＝（2，0），向量
＝（2，2），向量
＝（
cosα， sinα）则向量
与向量的夹角的范围为
【
】
A.[0，
] B.[，
] C.[，
] D.[
，]
8.若O为△ABC所在平面内一点，且满足
则一定有
【
】
A．
B．
C． 
D．
9、设坐标原点为O，抛物线y2＝2x与过焦点的直线交于A,B两个，则
等于
【 】
A．
B．－ C．3 D．－3
10．已知△ABC中，
S△ABC＝
,
则
与
的夹角为
A.300 B.－1500 C．1500 D．300或1500 【 】
11.若
那么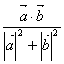
的取值范围是
【 】
A.(-∞,2) B.[0,
] C.[-,] D.
12．O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足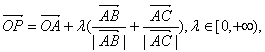
则P的轨迹一定通过△ABC的A．外心 B．内心 C．重心 D．垂心 【 】
二、填空题
13、已知a=(3,4),b⊥a且b的起点为(1,2),终点为(x,3x),则b=_______.
14、已知a=(2,－1),b=(λ,3).
1)若a与b的夹角为锐角,则λ的取值范围是________.
2)若a与b的夹角为钝角,则λ的取值范围是_________.
3)若a⊥b,则λ的取值范围是_________.
4)若a∥b,则λ的取值范围是_________.
15、已知点A(4,2)、B(－6,－4)、C(x,－2
)三点共线,则C点分AB的比
λ=____,x=_____.
16．已知I为△ABC的内心，当AB＝AC＝5，BC＝6时，
，则实数x、y的值为
.
三、解答题
17、已知：a=5,b=4,且a与b的夹角为60°,问当且仅当k为何值时,向量ka－b与a+2b垂直？
19．设平面内有两个向量
，
，且
，1）证明向量
与向量
垂直；2）若对于常数
）有
，求
的值。
20.平面上三个向量a、b、c的模均为1，它们相互之间的夹角均为120°.
（Ⅰ）求证：（a－b）⊥c；
（Ⅱ）若（ka+b+c）>1（k∈R），求k的取值范围.
18．已知向量
满足
的夹角为600，设向量
与向量
的夹角为θ（t∈R）.
(1) 若θ＝900，求实数t的值；
(2)若θ∈（900,1800）,求实数t的取值范围.
21．已知平面向量
若存在不同时为零的实数k和t,使 
（1）试求函数关系式k=f（t）;（2）求使f（t）>0的t的取值范围。
22．已知向量
①
;②求函数
的最小、最大值以及分别
取得最小、最大值时x的值．
③若