![]()
|
|
学科: 数学 |
| 教学内容:第三章 不等式 |
一、考纲要求
1.明确不等式的意义,掌握不等式的主要性质,并能正确灵活地应用这些性质解决问题.
2.在熟练掌握一元一次不等式(组)、一元二次不等式的解法的基础上掌握高次不等式和分式不等式的解法.
3.掌握一些简单的无理不等式的解法.
4.掌握一些简单绝对值不等式的解法.
5.掌握一些简单指数与对数不等式的解法.
6.能利用分类讨论的方法解含参数的不等式.
7.掌握不等式的证明,掌握证明不等式的比较法、综合法、分析法、数学归纳法、放缩法、反证法、换元法、判别式法.
8.掌握二个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理.
9.理解不等式|a|-|b|≤|a+b|≤|a|+|b|
二、知识结构
1.不等式的基本概念.
(1)两个实数a与b之间具有以下性质:如果a-b是正数,那么a>b;如果a-b是负数,那么a< b;如果a-b等于零,那么a=b,反过来也对.即:
a-b>0![]() a>b
a>b
a-b=0![]() a=b
a=b
a-b<0![]() a<b
a<b
(2)同解不等式:如果第一个不等式的解都是第二个不等式的解;并且第二个不等式的解也都是第一个不等式的解,那么这两个不等式叫做同解不等式.
2.不等式的性质
(1)基本性质
①a>b![]() b<a(对称性)
b<a(对称性)
②a>b,b>c![]() a>c(传递性)
a>c(传递性)
③a>b![]() a+c>b+c(加法单调性)
a+c>b+c(加法单调性)
④a>b,c>0![]() ac>bc
ac>bc
a>b,c<0![]() ac<bc(乘法单调性)
ac<bc(乘法单调性)
(2)运算性质
①a>b,c>d![]() a+c>b+d(同向不等式相加)
a+c>b+d(同向不等式相加)
②a>b,c<d![]() a-c>b-d(异向不等式相减)
a-c>b-d(异向不等式相减)
③a>b>0,c>d>0![]() ac>bd(同向不等式相乘)
ac>bd(同向不等式相乘)
④a>b>0,0<c<d![]()
![]() >
>![]() (异向不等式相除)
(异向不等式相除)
⑤a>b>0![]()
![]() >
>![]() (n
(n![]() Z,且n>1)(开方法则)
Z,且n>1)(开方法则)
⑥a>b>0![]() an>bn(n
an>bn(n![]() Z,且n>1)(乘方法则)
Z,且n>1)(乘方法则)
3.重要的基本不等式
(1)若a![]() R,则|a|≥0,a2≥0
R,则|a|≥0,a2≥0
(2)若a、b![]() R,则a2+b2≥2ab
R,则a2+b2≥2ab
(3)若a、b![]() R+,则
R+,则![]() (当且仅当a=b时等号成立)
(当且仅当a=b时等号成立)
(4)若a、b、c![]() R+,则
R+,则![]() (当且仅当a=b=c时等号成立)
(当且仅当a=b=c时等号成立)
(5)a>0时
|x|>a![]() x2>a2
x2>a2![]() x<-a或x>a
x<-a或x>a
|x|<a![]() x2<a
x2<a![]() -a<x<a
-a<x<a
(6)若a、b![]() R,则||a|-|b||≤|a±b|≤|a|+|b|
R,则||a|-|b||≤|a±b|≤|a|+|b|
4.解不等式的基本思想是化归为一元一次或一元二次不等式,主要依据是不等式的基本性质 ,要特别注意等价转化.
①![]() >a
>a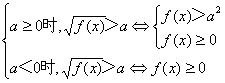
②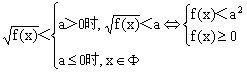
③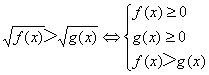
④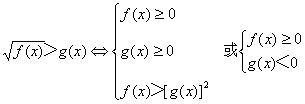
⑤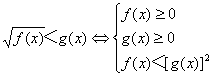
(6)指数不等式:转化为代数不等式.
af(x)<ag(x)(a>1)![]() f(x)<g(x);
f(x)<g(x);
af(x)<ag(x)(0<a<1)![]() f(x)>g(x);
f(x)>g(x);
af(x)<b(a>0,b>0,a≠b) ![]() f(x)·lga=lgb
f(x)·lga=lgb
(7)对数不等式,转化为代数不等式.
logaf(x)<logag(x)(a>1) ![]() 0<f(x)<g(x)
0<f(x)<g(x)
logaf(x)<logag(x)(0<a<1)![]() f(x)>g(x)>0
f(x)>g(x)>0
(8)含有绝对值符号不等式
|f(x)|<a(a>0)![]() -a<f(x)<a
-a<f(x)<a
|f(x)|>a(a>0)![]() f(x)>a或f(x)<-a
f(x)>a或f(x)<-a
另外,对于含有参数的不等式,要能正确地运用分类讨论方法求解.
5.证明不等式
不等式的证明的方法很多,主要应掌握比较法、分析法与不等式的解法
(1)一元一次不等式ax>b
①a>0时,解集为{x|x>a}
②a<0时,解集为{x|x<a}
③a=0时,(ⅰ)b≥0,解集为Φ;(ⅱ)b<0,解集为R
(2)一元二次不等式:(如下表)其中a>0,x1,x2是二次三项式ax2+bx+c=0的两实根,且x1<x2
| 类 型 解 集 | ax2+bx+c>0 | ax2+bx+c≥0 | ax2+bx+c<0 | ax2+bx+c≤0 |
| Δ>0 | {x |x<x1或x>x2} | {x|x≤x1或x≥x2} | {x|x1<x<x2 | {x|x1≤x ≤x2} |
| Δ=0 | {x|x≠- | R | Ф | {x|x=- |
| Δ<0 | R | R | Φ | Φ |
(3)简单的一元高次不等式:可用区间法(或称根轴法)求解,其步骤是:
①将f(x)的最高次项的系数化为正数;
②将f(x)分解为若干个一次因式的积;
③将每一个一次因式的根标在数轴上,从右上方依次通过每一点画曲线;
④根据曲线显示出的f(x)值的符号变化规律,写出不等式的解集.
(4)分式不等式:先整理成一般形式![]() >0或
>0或![]() ≥0的形式,转化为整式不等式求解,即:
≥0的形式,转化为整式不等式求解,即:
![]() >0
>0![]() f(x)·g(x)>0
f(x)·g(x)>0
![]() ≥0
≥0![]()
![]()
然后用“根轴法”或化为不等式组求解.
(5)无理不等式:转化为有理不等式求解,常见类型有数学归纳法,另外,对反证法,放缩法和判别式法利用函数单调性等方法也应明确.
A.比较法:
a.求差比较法:a>b![]() a-b>0;a<b
a-b>0;a<b![]() a-b<0;a=b
a-b<0;a=b![]() a-b=0
a-b=0
b.求商比较法:b>0,![]() >1
>1![]() a>b;b<0,
a>b;b<0,![]() >1
>1![]() a<b
a<b
步骤:作差(或商)![]() 变形
变形![]() 判断.
判断.
B.综合法
利用某些已经证明的不等式作为基础,再运用不等式的性质推导出所求证的不等式,这种证明方法叫综合法.综合法的思索路线是“由因导果”,也就是从一个(组)已知的不等式出发,不断地用必要条件代替前面的不等式,直至推导出要求证的不等式.
常用性质有:
a.(a+b)2≥0;
b.若a、b∈ R,a2+b2≥2ab(当且仅当a=b时取等号);
c.若a>0,b>0,c>0,则有:
a+b≥2![]() (当且仅当a=b时取等号);
(当且仅当a=b时取等号);
a+b+c≥3![]() (当且仅当a=b=c时取等号);
(当且仅当a=b=c时取等号);
a3+b3+c3≥3abc(当且仅当a=b=c时取等号).
C.分析法:
从求证的不等式出发,分析使这个不等式成立的充分条件把证明这个不等式的问题转化为这 些条件是否具备的问题.如果能够肯定这些条件都已具备,那么就可以判定所求证的不等式 成立,这种证明方法叫分析法,分析法的思索路线是“执果索因”,即从求证的不等式出发,不断地用充分条件来代替前面的不等式,直至找到已知不等式为止.
6.不等式的应用
利用不等式求最值,主要利用公式
![]() ,其中ai>0(i=1,2,…n)
,其中ai>0(i=1,2,…n)
(1)当a1+a2+…+an=m(常数)时,乘积a1·a2…an有最大值,其最大值为(![]() )n,当且仅当a1=a2=…=an时取最大值.
)n,当且仅当a1=a2=…=an时取最大值.
(2)当a1·a2…an=N(常数)时,和a1+a2+…+an有最小值,其最小值为n![]() ,当且仅当a1=a2=…=an时取最小值.
,当且仅当a1=a2=…=an时取最小值.
利用此公式求最值,必须同时满足下面三个条件:
①各项均为正数;
②其和或积为常数;
③等号必须成立.
利用此公式求最值,只需掌握n=2,3时的情形.
三、知识点、能力点提示
(一)“相等”与“不等”的关系
“相等”和“不等”是现实世界物质形式中量与量的两种重要的关系,它们是相互关联,相互依存的,在一定的条件下,互相转化.在数学学习过程中,要注意“相等”与“不等”的相互关系,抓住实质性联系,通过“相等”与“不等”的转化,找到解决问题的途径,达到解决问题的目的.为便于说明,举例如下:
1.“相等”与“不等”相互转化.
a)“相等”向“不等”的转化
例1 在ΔABC中,已知lgtgA+lgtgc=2lgtgB.求证:![]() ≤B<
≤B<![]() .
.
这个问题的已知是三角形中量的一种相等关系,要求从相等的条件出发,去推证出关于另一 (些)量的不等关系.虽说本题考查的是对数、三角函数、不等式的一些相关基础知识,并要求把分析法、综合法加以综合运用,但问题的实质却是某种“相等关系”向“不等关系”的转化,抓住这一实质特征,就可以找到解决问题的方法.当然要熟练掌握对数、三角函数及不等式的知识,在这里根据题意激活知识也是必不可少的.
简解:lgtgA+lgtgC=2lgtgB=lgtgA·tgc![]() tg2B=tgA·tgc
tg2B=tgA·tgc
tgB=tg(π-(A+C))=-![]()
∴tgA+tgC=tgB(tg2B-1)
∵tgA+tgC≥2![]() =2tgB
=2tgB
即 tg2B-1≥2
∴tgB≥![]() ∵B≥
∵B≥![]() ……
……
这里,抓住了tg2B=tgA·tgC这一相等关系及tgB=-![]() 隐含关系.通过tgA+tgC≥2
隐含关系.通过tgA+tgC≥2![]() 这一恒成立的不等式得出关于tgB的不等式,求解即得结论.
这一恒成立的不等式得出关于tgB的不等式,求解即得结论.
b)“不等”向“相等”的转化.
ⅰ)由实数理论知:若a≥b且a≤b则必有a=b,这是由“不等”变为“相等”的典型模型,在数学运算中经常用到,例如:由(x-y)2≤0及隐含条件(x-y)2≥0可以导出(x-y)2=0
ⅱ)添加变量使“不等”变“相等”.例如:由x+y>0![]() y>-x可含y=-x+t,这里t>0,从而把x,y的“不等”关系转化为某种“相等”关系.
y>-x可含y=-x+t,这里t>0,从而把x,y的“不等”关系转化为某种“相等”关系.
例2 已知a、b、c∈R,函数f(x)=ax2+bx+c,g(x)=ax+b ,当-1≤x≤1时,f(x)≤1
(1)证明:当|x|≤1时,|g(x)|≤2
(2)设a>0,当|x|≤1时,g(x)的最大值是2,求f(x).
本题综合了函数、方程、不等式的知识与方法,由于是以证明不等式为主,对逻辑思维和推理论证能力的要求很高,难度很大,它以二次函数和一次函数为载体,侧重考查函数的概念,含绝对值的不等式的性质,函数的单调性等数学知识的综合灵活运用,并利用函数作为材料,考查恒等变形,放缩变形的方法和技能,等式和不等式的联系和转化.这里仅剖析第(2)小题.
已知告诉我们:对一切x∈[-1,1],g(x)≤2恒成立,这是不等的关系,由此(加上“a>0 ”)要得出f(x)的表达式,即给出一组值,使之分别与a、b、c相等,很明显是“不等”向“ 相等”的转化.
简解如下:
∵a>0,∴g(x)=ax+b是[-1,1]上的增函数,当x=1时,g(x)max=g(1)
即:a+b=g(1)=2=f(1)-f(0) ①
∵-1≤f(0)=f(1)-2≤1-2≤-1
∴c=f(0)=-1
∵当-1≤x≤1 时f(x)≥-1恒成立,即f(x)≥f(0)
∴直线x=0是抛物线y=f(x)的对称轴,由此可得-![]() =0,即b=0代入①得a=2
=0,即b=0代入①得a=2
∴f(x)=2x2-1
2.“相等”与“不等”的构造
从上可以看出,“相等”向“不等”的转化,其关键之处在于构建出相关的不等关系,再将这个不等关系向目标(不等式)作进一步的变形处理即可.
a)在“相等关系”中构造出“不等关系”:
途径:①利用重要不等式:ⅰ)a2+b2≥2ab ⅱ)a、b、c∈R+,
a+b≥2![]() ,a+b+c≥3
,a+b+c≥3![]() ⅲ)
ⅲ)![]() +
+![]() ≥2(a、b>0)等等
≥2(a、b>0)等等
②利用函数单调性:f(x)是区间I上的增函数,若x1、x2∈I,则f(x2 )<f(x1);f(x)是区间I上的减函数,若x1、x2∈I,则f(x1)>f(x2);
③利用等量关系中的隐含条件,如
y=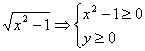 x2+y2=a2
x2+y2=a2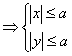
例3 已知a、b为正数,且a+b=1,求证(a+![]() )2+(b+
)2+(b+![]() )2≥(
)2≥(![]() ).
).
证明一 因a、b为正数,a+b=1,于是
(a+![]() )2+(b+
)2+(b+![]() )2
)2
=(a+![]() )2+(b+
)2+(b+![]() )2
)2
=(a+1+![]() )2+(b+1+
)2+(b+1+![]() )2
)2
=a2+1+![]() +2a+2b+2·
+2a+2b+2·![]() +b2+1+
+b2+1+![]() +2b+2a+2·
+2b+2a+2·![]()
=6+(a2+b2)+( ![]() +
+![]() )+2(
)+2(![]() +
+![]() )
)
=6+(a+b)2-2ab+(![]() )+2(
)+2(![]() )+
)+![]() ≥13-2ab
≥13-2ab
由![]() ≤
≤![]() =
=![]() 得,ab≤
得,ab≤![]()
所以13-2ab≥![]()
故 (a+![]() )2+(b+
)2+(b+![]() )2≥
)2≥![]() (当且仅当a=b=
(当且仅当a=b=![]() 时取等号)。
时取等号)。
证明二 由定理a2+b2≥2ab,易得a2+b2≥![]() ,于是
,于是
(a+![]() )2+(b+
)2+(b+![]() )2≥
)2≥![]() (a+
(a+![]() +b+
+b+![]() )2
)2
=![]() 〔(a+b)+
〔(a+b)+![]() 〕2=
〕2=![]() (1 +
(1 +![]() )2
)2
由 ![]() ≤
≤![]() =
=![]() ,得ab≤
,得ab≤![]() 又有
又有![]() ,即
,即![]() ≥4
≥4
例4 求满足(x2+2x+3)(y2+1)=2的实数x,y
解:∵x2+2x+3=(x+1)2+2≥2 y2+1≥1
∴(x2+2x+3)(y2+1)≥2 当且仅当x2+2x+3=2,y2+1=1时成立
解之得x=-1且y=0
b)在“不等”关系中构造“相等”关系.
途径:①设元构造.例:x2+y2≤1![]()
②数形结合,构造函数(或方程).例:![]() ≥x可设y1=
≥x可设y1=![]() ,y2=x
,y2=x
例5 求证:![]() (n∈N,n≥2)
(n∈N,n≥2)
证明:∵2n=(1+1)n=1+n+![]() +…
+…
∴n≥2,n∈N,右端展开式中的各项为正
∴2n>![]()
即![]() <
<![]()
例6 为使不等式x2+4xy+4y2+10x+ay+b>0对任意实数x、y恒成立,求 实数a、b应满足的条件.
解:为使不等式恒成立,须且仅须x2+4xy+4y2+10x+ay+b为一个实数的平方加上一个正增量t,可令x2+4xy+4y2+10x+ay+b=(x+2y+m)2+t=x2+4xy+4y2+2mx+4my+m2+t
根据多项式相等的条件有: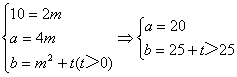
所以当a=20,b>25时,原不等式恒成立.
例7 已知x2+y2≤1,求x+y的最大值.
分析:这里,量x+y与x2+y2的直接关系可以通过2(x2+y2)≥(x+y)2得出,还可以通过换元令x=rcosθ,y=rsinθ,则有r2≤1
∴0≤r≤1
∴x+y=rcosθ+rsinθ=![]() rsin(θ+
rsin(θ+![]() )≤
)≤![]() r≤
r≤![]() 得出.
得出.
3.由不等进行估算
估计变数或式子的取值范围,对某些数学问题能起到挖掘隐含信息,找到思维的切入点,从而使困难的问题迎刃而解.
例8 求解方程组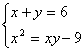
这是二个方程三个变量的方程组,按常规似乎有无数个解.但可对xy进行估算,可知xy>9 ,否则z2<0,x+y>0
∵x>0,且y>0且6=x+y≥2![]() xy≤9故z2=xy-9≤9-9=0
xy≤9故z2=xy-9≤9-9=0
∴z=0且x=y=3
4.由不等推出矛盾:
反证法是“数学家最精良的武器之一”,它在数学解题中确有奇效,若能有意识地挖掘问题中潜在的不等关系,使两者联手,往往可以及时找到矛盾点——由不等导出矛盾.
例9 已知锐角α,β满足![]() +
+![]() =2,求证α+β=
=2,求证α+β=![]()
证明:假设α+β>![]() ,则α>
,则α>![]() -β,β >
-β,β >![]() -α
-α
∵α,β,![]() -2,
-2,![]() -βε(0,
-βε(0,![]() )
)
∴cosα<cos(![]() -β)=sinβ
-β)=sinβ
cosβ<cos(![]() -α)=sinα
-α)=sinα
从而2=![]() +
+![]() <
<![]() =2矛盾
=2矛盾
故α+β≤![]() ,同理α+β≥
,同理α+β≥![]() ,∴α+β=
,∴α+β=![]()
(二)不等式与函数、方程的关系
前面谈到“不等”与“相等”的相互依存,转化,在不等式与函数、方程中尤为突出.
1.一元二次不等式与二次函数,一元二次方程的关系
(1)一元二次方程的根(二次函数图像与x轴交点的横坐标)是对应一元二次不等式解集的端点值,由此可引申出解一元高次不等式的“根轴法”,可以由数形结合,根据函数图像求不等式的解集.
(2)方程的条件根问题可以借助所设辅助函数与关于函数值的不等式,得出等价转化.
例10 解不等式![]() <2logax-1(a>0,a≠1)。
<2logax-1(a>0,a≠1)。
本小题主要考查对数函数的性质,对数不等式,无理不等式解法等基础知识,考查分类讨论 的思想。
解 原不等式等价于
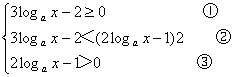
由①得 logax≥![]() ,
,
由②得 logax<![]() ,或logax>1
,或logax>1
由③得 logax>![]() ,
,
由此得 ![]() ≤logax<
≤logax<![]() ,或logax>1
,或logax>1
当a>1时得所求的解是{x|![]() }∪{x|x>a|};
}∪{x|x>a|};
当0<a<1时得所求的解集是
{x|![]() }∪{x|0<x<a}
}∪{x|0<x<a}
2.不等式与函数最值
(1)求函数的最大值与最小值涉及的范围极为广泛,可使用的方法很多,代数的,三角的,几何的问题中都有大量的求最值问题,求函数的值域也常归结为函数的最值;许多实际问题的应用题也能利用最值解决.
而最值问题往往归结为不等问题,用不等式的性质以及求解不等式的方法都可用于解决最值问题,代数课本上册P26例2实际上是两个极值定理,有着广泛的应用价值,(课本上虽为二个正数,但可推广到三、四个及多个的情形)在利用它解决问题时,要注意三个条件“一正
、二定、三能等”即:①这几个数都必须是正数.例如:当xy=4,如果没有x、y都为正数这个条件,就不能说x+y有最小值4,因为若x=y=-2虽满足xy=4但x+y=-4<4.②这几个数必须满 足条件“和为定值”或“积为定值”,如果找不出“定值”这个条件,就不能应用这两个定
理.例如:当x>0时,求y=x2+![]() 的最小值,若写成y=x2+
的最小值,若写成y=x2+![]() ≥2
≥2![]() (等号当且仅当x2=
(等号当且仅当x2=![]() 即x=1时ymin=2
即x=1时ymin=2![]() =2)则最小值为2,这是错误的. 而应该是这样的:由于x2·
=2)则最小值为2,这是错误的. 而应该是这样的:由于x2·![]() 为定值, 故y=x2+
为定值, 故y=x2+![]() =x2+
=x2+![]() =
=![]() ,即ymin=
,即ymin=![]() (显然(
(显然(![]() )3=
)3=![]() <8 即
<8 即![]() <2
<2![]()
③要保证等号能成立,如果等号不能成立,则求出的仍不是最值,例如:当0<x<![]() 时求y=sinx+
时求y=sinx+![]() 的最小值,尽管y=sinx+
的最小值,尽管y=sinx+![]() ≥2
≥2![]() =4.但ymin=4是错误的,因为当sinx=
=4.但ymin=4是错误的,因为当sinx=![]() 时可推出sinx=2(sinx>0)不成立,这只能说y> 4恒成立,因此ymin>4必成立,实际上由y=t+
时可推出sinx=2(sinx>0)不成立,这只能说y> 4恒成立,因此ymin>4必成立,实际上由y=t+![]() 在(0,1]上是
单调减函数可知,当sinx=1时ymin=5
在(0,1]上是
单调减函数可知,当sinx=1时ymin=5
(2)不等式与二次函数y=ax2+bx+c(a≠0)的最值
x∈R时
①当a>0时,x=-![]() 时,ymin=
时,ymin=![]() ;当a<0,x=-
;当a<0,x=-![]() 时ymax=
时ymax=![]()
②当xε[m,n](m<n)时,易画出图像(是抛物线的一部分)“看图说话”.
例11 若a>0,y=ax2+bx+c的最值如下表
| n≤- | m≤- |
| m≥- | |
| 最大值 | f(m) | f(m) | f(n) | f(n) |
| 最小值 | f(n) | f(- | f(- | f(m) |
当a<0时,可依上表写出类似结论.
(3)重要函数y=x+![]() ,(a>0,x>0)的单调性.
,(a>0,x>0)的单调性.
利用不等式的性质可证明,y=x+![]() 在(o,
在(o,![]() )上是减函数,在 QS[
)上是减函数,在 QS[![]() ,+∞)上是增函数.
,+∞)上是增函数.
例12 已知f(x)=x2+ax+b,-1≤x≤1,若|f(x)|的最大值是M。证明:M≥![]() .
.
证明 抛物线f(x)=x2+ax+b的顶点坐标是(-![]() ,
,![]() ),且f(1)=a+b+1, f(-1)=-a+b+1。
),且f(1)=a+b+1, f(-1)=-a+b+1。
(1)若|-(![]() )|>1,则M应是|f(-1)|与|f(1)|中最大的一个。 | f(-1)|+|f(1)|≥|f(1)-f(-1)|=2|a|>4
)|>1,则M应是|f(-1)|与|f(1)|中最大的一个。 | f(-1)|+|f(1)|≥|f(1)-f(-1)|=2|a|>4
得|f(-1)|、|f(1)|中必有一个大于![]() 者。
者。
(2)若|-![]() |≤1,则M应是|f(-1)|、|f(1)|、|
|≤1,则M应是|f(-1)|、|f(1)|、|![]() |中最大的一个。
|中最大的一个。
①若b≥-![]() ,则|f(1)|+|f(-1)|≥|f(1)+f(-1)|=|2+2b|≥1, 故在|f(-1)|与|f(1)|中必有一个大于等于
,则|f(1)|+|f(-1)|≥|f(1)+f(-1)|=|2+2b|≥1, 故在|f(-1)|与|f(1)|中必有一个大于等于![]() 。
。
②若b<-![]() ,则△=a2-4b>0,|
,则△=a2-4b>0,|![]() |=
|=![]() -b≥-b>
-b≥-b>![]() ,故必有M>
,故必有M>![]() 。
。
综上,M≥![]() 总成立。
总成立。
(三)不等式与几何的关系
数学关系实质上是反映现实生活中的量与量的关系的,因而往往具有一些实际意义(或几何意义),不等关系也是这样.
1.构造几何图形证明不等式
1)对于一些含有“A+B≥C”结构的不等式问题,可联想“三角形两边之和大于第三边.”构造三角形证明
例13 x、y、zεR+,求证:![]()
简析:
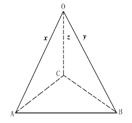
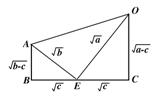
由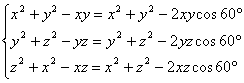 联想到余弦定理,构造三棱锥
联想到余弦定理,构造三棱锥
o-ABC得证(如图),AB=![]() BC=
BC=![]() CA=
CA=![]() 及ΔABC中,AB+BC>AC
及ΔABC中,AB+BC>AC
2)对于一些含有“A·B或![]() (A+B)·C”结构的不等式问题,可联想面积证明之
(A+B)·C”结构的不等式问题,可联想面积证明之
例14 设a>c,b>c>0,求证:![]()
简析:∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2
)2
(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2即勾股定理,
)2即勾股定理,
![]() =
=![]() (
(![]() +
+![]() )联想到梯形面积可用补形法构造一个梯形.(如右图)
)联想到梯形面积可用补形法构造一个梯形.(如右图)
3)对于含有“a2+b2+c2”结构的不等式问题,可联想长方体中的对角线与棱长的公式,构造长方体.
4)对于一些含有“(a-m)2+(b-n)2”或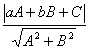 ”结构的不等式问题可用解几中的两点间的距离,点到直线的距离公式进行构图求证.
”结构的不等式问题可用解几中的两点间的距离,点到直线的距离公式进行构图求证.
5)对含有“a2+b2=R2且aA+bB+C=0”结构的不等问题,可构造圆与直线的位置关系求 证.
2.运用不等式知识解决几何最值
这类问题主要是通过建立目标函数之后,应用不等式知识(如函数单调性,基本不等式等)求 出函数最值,这里不作详述.
(四)不等式与其它杂题
1.不等关系的探索.
现实生活中量与量的不等关系是普遍的、大量的,高考中探索性问题即包含对不等关系的探索,下面举例说明之:
例15 已知Sn=1+![]() +
+![]() +…
+…![]() (n∈N),设f(n)=S2n+1-Sn+1.试确定m的取值范围,使得对于一切大于1的自然数,不等式f(n)>m恒成立.
(n∈N),设f(n)=S2n+1-Sn+1.试确定m的取值范围,使得对于一切大于1的自然数,不等式f(n)>m恒成立.
分析:依题意f(n)=S2n+1-Sn+1=![]() +
+![]() +…+
+…+![]() (n∈N)由于f(n)无法求和化简,故应把f (n)看作n的函数,只须求出f(n)的最小值即可.
(n∈N)由于f(n)无法求和化简,故应把f (n)看作n的函数,只须求出f(n)的最小值即可.
略解:∵f(n)= ![]() +
+![]() +…+
+…+![]() , f(n+1)=
, f(n+1)=![]() +…+
+…+![]()
且f(n+1)-f(n)= ![]() +
+![]() -
-![]() =(
=(![]() -
-![]() )+(
)+(![]() -
-![]() )>0
)>0
∴f(n+1)>f(n) (n>1,n∈N)
∴f(2)是f(n)(n>1,n∈N)的最小值f(2)=![]()
要使f(n)>m恒成立,只须f(2)>m恒成立,故m<![]()
例16 已知等差数列{an}和等比数列{bn}中,a1=b1,a2=b 2,a1≠a2,an>0,n∈N
(1)试比较a3,b3及a4,b4的大小.
(2)推测an与bn的大小,并证明你的结论.
(结论:bn>an对任意n![]() N,n≥3成立)
N,n≥3成立)
简析:运用归纳法进行探测,猜出一般性的结果,用数学归纳法证明之.
例17 定义在(-1,1)上的函数f(x)满足(ⅰ)对任意x、yε(- 1,1)有f(x)+f(y)=f(![]() ) (ⅱ)当xε(-1,0)时,有f(x)>0,试研究f(
) (ⅱ)当xε(-1,0)时,有f(x)>0,试研究f(![]() )+ f(
)+ f(![]() )+…+f(
)+…+f(![]() )与f(
)与f(![]() )的关系.
)的关系.
简析:由(ⅰ)、(ⅱ)可知f(x)是(-1,1)上的奇函数且是减函数.
f(![]() )=f(
)=f(![]() )
)
=f(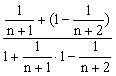 )
)
=f![]()
=f![]()
∴f(![]() )+f(
)+f(![]() )+…+f(
)+…+f(![]() )
)
=[f(![]() )-f(
)-f(![]() )]+[f(
)]+[f(![]() )-f(
)-f(![]() )]
)]
+…+[f(![]() )-f(
)-f(![]() )]
)]
=f(![]() )-f(
)-f(![]() )>f(
)>f(![]() )
)
(∵0<![]() <1,∴f(
<1,∴f(![]() )<0)
)<0)
2.不等式问题中的思维策略
1)反客为主
当从正面按常规方法不易得出问题的解时,可以变换角度从侧面入手寻找突破口.
例18 当|p|≤2时,不等式2x-1>p(x2-1)恒成立,求x的取值范围
简析:若按常规思路,将问题转化为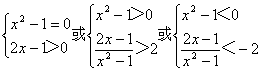 分别解三个不等式组获解,但太繁琐.
分别解三个不等式组获解,但太繁琐.
若“反客为主”将原不等式化为关于P的不等式:
(1-x2)p+(2x-1)>0构造函数f(p)=(1-x2)p+2x-1
问题转化为对一切|p|≤2,f(p)>0恒成立
当1-x2=0时易得x=1
当1-x2≠0时,当且仅当![]() 解之得
解之得![]() <x<
<x<![]() 且x≠1
且x≠1
综上 ![]() <x<
<x<![]()
2)以退为进
有时从问题的整体去思考颇为费解,但若退出局部着手,常能轻易找出问题的解决途径.
例19 在锐角ΔABC中,求证:sinA+sinB+sinC>cosA+cosB+cosC
简析:观察此题,求证式整体与局部,三个角的三角函数有轮换的特征可退出局部考察A、B 的关系是否有sinA>sinB
证明:∵A+B=π-C>![]()
∴![]() >A>
>A>![]() -B>0
-B>0
∴sinA>sin(![]() -B)=cosB
-B)=cosB
同理 sinB>cosC
sinC>cosA
三式相加得sinA+sinB+siC>cosA+cosB+cosC

【同步达纲练习】
1.某广场中心要建一灯柱,广场边缘A点距灯柱根部(B点)100米,已知该点的照明亮度I和灯 光射到这点的光线与地面夹角θ的正弦成正比,和这点的光源P的距离r的平方成反比,若要 使A点获得最好的照明亮度,灯柱应建多高?(精确到0.1米)
本题考查三角函数、立体几何解决实际问题的能力,同时考查数形结合思想、成比例的概念 ,利用不等式求最值的方法.
2.已知xn=sin2θ1·sin2θ2·sin2θ3…sin2θn
yn=1-(cos2θ1+cos2θ2+…+cos2θn)(n![]() N)
N)
(1)判断x1与y1,x2与y2的大小关系,加以证明.
(2)猜想xn与yn的关系,并证明你的结论.
(3)若cosθn=(cos![]() )n+1,证明xn>
)n+1,证明xn>![]() .
.
本题考查三角函数的恒等变形,不等式的证明及观察、归纳由特殊到一般的推理能力.
3.已知如图。为处理含有某种杂质的污水, 要制造一宽2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,问当a、b各 为多少米时,经沉淀流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)。
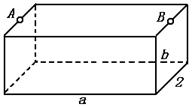
4.甲乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过C 千米/时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度V(千米/时)的平方成正比,且比例系数b;固定部分为a元。
(1)把全程运输成本y(元)表示为速度V(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
本题考查由实际问题转化为等比数列的能力,及求函数最值的方法,建立数学模型的能力, 阅读理解能力.
5.已知f(x)=x2+(lga+2)x+lgb,f(-1)=-2,且对任何实数都有f(x)≥2x,求a、b的值.
本题考查一元二次不等式恒成立的充要条件和实数的性质,及由“不等”向“相等”转化的能力.
6.渔场中鱼群的最大养殖量为m吨,为保证鱼群的生长空间,实际养殖量不能达到最大养殖 量,必须留出适当的空闲量,已知鱼群的年增长量y吨和实际养殖量x吨与空闲率的乘积成正 比,比例系数为k(k>0)
(1)写出y与x的函数关系式,并指出这个函数的定义域.
(2)求鱼群的年增长量达到的最大值.
(3)当鱼群的年增长量达到最大值时,求k的取值范围.
本题考查二次函数区间上的最值,及不等式的实际应用.
7.m为何值时,关于x的方程x2-2(m+2)x+m2-1=0,(1)有两个正根;(2)有两个大于2的根;(3)一根在(0,1)内,另一根在(1,2)内.
本题考查一元二次方程二次函数的图像,应用不等式与它们的关系进行问题转化的能力.
8.已知f(x)=x2+ax+b,求证:|f(1)|、|f(2)|、|f(3)|中至少有一个不小于![]() 。
。
本题考查不等式的运用.
9.求![]() ·
·![]() =7850中的数字x,y,z.(
=7850中的数字x,y,z.(![]() 表示该数百位数为a,十位数为b,个位数为c)
表示该数百位数为a,十位数为b,个位数为c)
本题考查整数及不等式知识,由相等向不等的转化.
10.已知a>0且a≠1,关于x的不等式ax>1的解集是{x|x<0}。求关于x的不等式loga(x-![]() )>0的解集.
)>0的解集.
本题考查不等式的解法.
11.若正整数p、q、r使方程px2-qx+r=0在区间(0,1)内有两个不同的实根,求p的最小值 .
本题考查方程,不等式知识,分析问题解决问题的能力.
12.边长为5的菱形,它的一条对角线的长不大于6,另一条对角线的长不小于6,则这个菱形 两对角线长度之和的最大值是多少?
本题考查几何极值与不等式的应用.
13.某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池由于地形限 制,长宽都不能超过16米,如果池四周围壁建造单价为每米长400元,中间两道隔墙造单价 为每米长248元,池底建造单价为每平方米80元,池壁的厚度忽略不计,试设计水池的长和 宽,使总造价最低,并求出总造价.(45000元)
本题考查均值不等式,函数的单调性及用之求最值,建模能力,分析解决问题的能力.
14.某地耕地10 000公顷,规化十年后粮食单产比现在增加22%,人均 粮食占有量比现在提高10%,如果人口增长率为1%,那么耕地平均每年至多只能减少多少公 顷(精确到1公顷)?(粮食单产=![]() ,人均粮食占有量=
,人均粮食占有量=![]() )
)
本题考查建模能力,不等式与数列知识
15.试用几何法证明:![]() ≥
≥![]() (a>0,b>0)
(a>0,b>0)
本题考查不等式的几何意义,构图法.

参考答案
【同步达纲练习】
1.解:设灯柱高为h米,由题意
I=k·sinθ/r2(k为正常数)
r=100/cosθ
∴I2=k2·sin2θ/(100/cosθ)4=k2sin2θcos4θ/108
=![]() ·(2sin2θ)(cos2θ)(cos2 θ)
·(2sin2θ)(cos2θ)(cos2 θ)
≤![]()
=![]() (定值)
(定值)
当且仅当2sin2θ=cos2θ 即tgθ=![]() /2时等式成立.
/2时等式成立.
A点照明度最好,这时h=AB·tgθ=100×![]() =50
=50![]() =70.7米
=70.7米
故为使A点获得最好的照明亮度,灯柱的高应为70.7米.
2.解(1):x1=sin2θ1,y1=1-cos2θ1=sin2θ1 ∴x1=y1
x2=sin2θ1sin2θ2,y2=1-(cos2θ1+cos2θ2)
x2-y2=sin2θ1sin2θ2-sin2θ1+cos2θ2
=-sin2θ1cos2θ2+cos2θ2
=cos2θ2·cos2θ1≥0
∴ x2≥y2≥2
(2)猜想xn≥yn
证明:当n=1时,不等式成立,假设当n=k时xk≥yk成立,即sin2θ1sin2θ2……sin2![]() k≥1-(cos2θ1+cos2θ2+…+cos2θk)
k≥1-(cos2θ1+cos2θ2+…+cos2θk)
则xk+1=sin2θ1sin2θ2…sin2k·sin2θk+1≥
[1-(cos2θ1+cos2θ2+…+cos2θk)]sin2θk+1
=[1-(cos2θ1+cos2θ2+…+cos2θk)][1-cos2θk+1]
=[1-(cos2θ1+cos2θ2+…+cos2θk+cos2θk+1)]+cos2θk+ 1(cos2θ1+cos2θ2+…+cos2θK)
≥1-(cos2θ1+cos2θ2+…+cos2θk+cos2θk+1)
=yk+1
∴n=k+1时,不等式成立.
故对n![]() N,都有xn≥yn
N,都有xn≥yn
(3)xn≥yn=1-(cos2θ1+cos2θ2+…+cos2θn)
=1-[(![]() )2+(
)2+(![]() )3+…+(
)3+…+(![]() )n+1]
)n+1]
=1-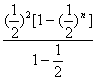
=1-![]() +(
+(![]() )n+1>
)n+1>![]()
3.解法一 设y为流出的水中杂质的质量分数,则y=![]() ,其中k>0为比
例系数。依题意,即所求的a、b值使y最小。
,其中k>0为比
例系数。依题意,即所求的a、b值使y最小。
根据题设有4b+2ab+2a=60(a>0,b>0)
得b=![]() {0<a<30
{0<a<30![]() ①
①
于是 y=![]() =
=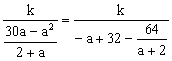
≥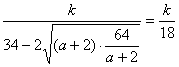
当a+2=![]() 时取等号,y达到最小值
时取等号,y达到最小值
这时a=6,a=-10(舍去),将a=6代入①得b=3
故当a为6为,b=3为是时,经沉淀后流出的水中该杂质的质量分数最小。
解法二 依题意,即所求的a、b值使ab最大。
由题设知4b+2ab+2a=60(a>0,b>0),即a+2b+ab=30
因a+2b≥2![]()
所以2![]() +ab≤30
+ab≤30
当且仅当a=2b时,上式取等号
由a>0、b>0解得0<ab≤18
即当a=2b时,ab取得最大值,其最大值为18
2b2=18,解得b=3,a=6
故当a=6米,b=3米时,经沉淀后流出的水中该杂质的质量分数最小。
4.解:(1)依题意知汽车从甲地匀速行驶到乙地所用时间为![]() ,全程运 输成本为y=a·
,全程运 输成本为y=a·![]() +bV2·
+bV2·![]() =S(
=S(![]() +bV),
+bV),
故所求函数及其定义域为y=S(![]() +bV),V∈(0,c)
+bV),V∈(0,c)
(2)依题意知S、a、b、V都为正数,故有S(![]() +bV)≥2S
+bV)≥2S![]()
当且仅当![]() =bV,即V=
=bV,即V=![]() 时上式中等号成立
时上式中等号成立
若![]() ≤c,则当V=
≤c,则当V=![]() 时 ,全程运输成本y最小
时 ,全程运输成本y最小
若![]() >c,当V∈(0,c)时,有
>c,当V∈(0,c)时,有
S(![]() +bV)-S(
+bV)-S(![]() +bc)=s[(
+bc)=s[(![]() -
-![]() )+(bV-bc)]
)+(bV-bc)]
=![]() (c-V)(a-bcV)
(c-V)(a-bcV)
因c-V≥0,且a>b2c,
得a-bcV≥a-b2c>0,
所以 S(a![]() +bV)≥S(
+bV)≥S(![]() +bc),且仅当V=c时等号成
立,也即当V=c时全程运输成本最小
+bc),且仅当V=c时等号成
立,也即当V=c时全程运输成本最小
综上知,为使全程运输成本y最小,当![]() ≤c时,行驶速 度应为V=
≤c时,行驶速 度应为V=![]() ;当
;当![]() >c时,行驶速度应为V=c
>c时,行驶速度应为V=c
5.解:f(-1)=1-(lga+2)+lgb=-2即lga-lgb=1
∵f(x)≥2x对任何x都成立即x2+(lga+2)x+lgb≥2x恒成立
∴Δ=(lga)2-4(lga-1)≤0
∴lga=2
即a=100
代入lga-lgb=1 得b=10
6.解(1)由题意得y=kx(1-![]() ) (0<x<m)
) (0<x<m)
(2)y=-![]() (x-
(x-![]() )2+
)2+![]() ,当x=
,当x=![]() 时ymax=km/4
时ymax=km/4
(3)依题意有:0<x+y<m即0<![]() +
+![]() <m
<m
∴-2<k<2但k>0
∴0<k<2
7.解(1)∵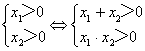
∴原方程有两正根的充要条件是
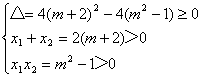
解得: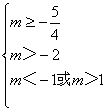
即当-![]() ≤m<-1或m>1时,原方程有两正根.
≤m<-1或m>1时,原方程有两正根.
(2)∵![]()
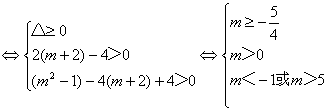
即当m>5时原方程有两个大于2的根.
(3)设f(x)=x2-2(m+2)x+m2-1,它的图像是开口向上的抛物线如图,方程f(x)=0的有两 实根x1,x2且满足0<x1<1<x2<2的充要条件是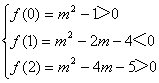
解得: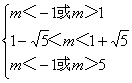
∴当1-![]() <m<-1时,及方程有两个实根,且一根位于(0,1)内,另一根位于(1, 2)内.
<m<-1时,及方程有两个实根,且一根位于(0,1)内,另一根位于(1, 2)内.
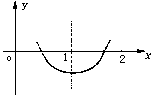
8.证明 假设|f(1)|、|f(2)|、|f(3)|均小于![]() ,
,
即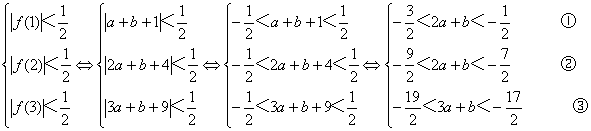 ①+③得-
①+③得-![]() 得-
得-![]() <2a+b<-
<2a+b<-![]() ,与②矛盾。
,与②矛盾。
故|f(1)|、|f(2)|、|f(3)|中至少有一个不小于![]() 。
。
9.解:∵![]() 表示一个百位数是3的三位数.
表示一个百位数是3的三位数.
∴300≤![]() <400
<400
∴![]() 即9<10x+5<27
即9<10x+5<27
∴x=2
∴![]() =
=![]() =
=![]() =314
=314
∴y=1,Z=4
10.因不等式ax>1的解集为{x|x<0},
故0<a<1。不等式loga(x-![]() )>0
)>0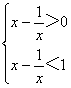
由此解得-1<x<![]() 或1<x<
或1<x<![]()
故原不等式的解集为{x|-1<x<![]() 或1<x<
或1<x<![]() }
}
11.解:依题意知: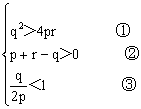
其中p,q,r![]() N
N
由②可设q=p+r-t,其中t≥1,代入①得p+r-t>2![]()
整理成(![]() )2-2
)2-2![]() +(
+(![]() )2-t>0即
)2-t>0即![]() >
>![]() +
+![]() (
(![]() <
<![]() ·
·![]() 与②③矛盾
与②③矛盾![]()
∴p>(![]() +
+![]() )2取r=t=1得p>(1+1)2=4
)2取r=t=1得p>(1+1)2=4
∴p≥5即Pmin=5
此时q=5,r=1
12.解:设菱形ABCD的对角线AC、BD相交于O点,AC≥6,BD≤6,则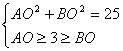 (1)令AO=3+x,BO=3-y(x≥0,y≥0)
(1)令AO=3+x,BO=3-y(x≥0,y≥0)
![]()
由(1)知,x,y不同时为零且x>0,AO2+BO2=(3+x)2+(3-y)2=25
即(x-y)2+6(x-y)+9=16-2xyx-y=±![]() -3
-3
AC+BD=2(3+x)+2(3-y)=12+2(x-y)
当且仅当y=0时,x-y取得最大值1,∴AC+BD的最大值是14.
13.解:设污水池长为x米,则宽为![]() 米,于是总造价为y=400(2x+
米,于是总造价为y=400(2x+![]() ×2)+248×2×
×2)+248×2×![]() +80×200=800(x+
+80×200=800(x+![]() )+16000,其中
)+16000,其中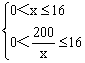 (若用x+
(若用x+![]() ≥2
≥2![]() =36,等号当且仅当x=
=36,等号当且仅当x=![]() 即x=18成立但x
即x=18成立但x![]() (0,16])
(0,16])
由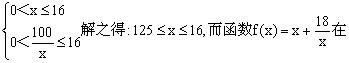
[12.5,16]上为减函数∴f(x)=x+![]() ≥16+
≥16+![]() =16+
=16+![]()
这时x=16 ∴y≥800(16+![]() )+16000=45000元,即最低造价为45000 元.
)+16000=45000元,即最低造价为45000 元.
14.设耕地平均每年至多只能减少x公顷,又设该地区现有人口为P人、粮食单产为M吨/公顷
依题意得不等式
![]()
![]() ×(1+10%)
×(1+10%)
化简得x≤103×[1-![]() ]
]
因
103×[1-![]() ]
]
=103×[1-(![]() )×(1+C110×0.01+C210×0.012+…)]
)×(1+C110×0.01+C210×0.012+…)]
≈103×[1-![]() ×1.1045]≈4.1
×1.1045]≈4.1
≤4(公顷)
15.证明:如图
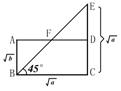
∵SΔBCE+SΔBAF≥S四边形ABCD(![]() =
=![]() 即D、E重合时
取等号)
即D、E重合时
取等号)
即![]() ≥
≥![]()
