不等式的概念和基本性质
重点:不等式的基本性质
难点:不等式基本性质的应用
主要内容:
1.不等式的基本性质
(1)a>b![]() b<a
b<a
(2)a>b,b>c![]() a>c
a>c
(3)a+b<c![]() a<c-b
a<c-b
a>b![]() a+c>b+c
a+c>b+c
(4)a>b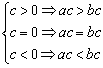
2.不等式的运算性质
(1)加法法则:a>b,c>d![]() a+c>b+d
a+c>b+d
(2)减法法则:a>b,c>d![]() a-d>b-c
a-d>b-c
(3)乘法法则:a>b>0,c>d>0![]() ac>bd>0
ac>bd>0
(4)除法法则:a>b>0,c>d>0![]()
![]() >
>![]() >0
>0
(5)乘方法则:a>b>0,an>bn>0 (n∈N, n≥2)
(6)开方法则:a>b>0,![]() >
>![]() >0 (n∈N, n≥2)
>0 (n∈N, n≥2)
3.基本不等式
(1)a∈R,a2≥0 (当且仅当a=0时取等号)
(2)a,b∈R,a2+b2≥2ab (当且仅当a=b时取等号)
(3)a,b∈R+,![]() ≥
≥![]() (当且仅当a=b时取等号)
(当且仅当a=b时取等号)
(4)a,b,c∈R+,a3+b3+c3≥3abc (当且仅当a=b=c时取等号)
(5)a,b,c∈R+,![]() ≥
≥![]() (当且仅当a=b=c时取等号)
(当且仅当a=b=c时取等号)
(6)a-b≤a±b≤a+b
4.不等式的概念和性质是进行不等式的变换,证明不等式和解不等式的依据,应正确理解和运用不等式的性质,弄清每条性质的条件与结论,注意条件与结论之间的关系。基本不等式可以在解题时直接应用。
例1.对于实数a,b,c判断以下命题的真假
(1)若a>b, 则ac<bc; (2)若ac2>bc2, 则a>b;
(3)若a<b<0, 则a2>ab>b2;
(4)若a<b<0, 则a>b;
(5)若a>b, ![]() >
>![]() , 则a>0, b<0.
, 则a>0, b<0.
解:(1)因为c的符号不定,所以无法判定ac和bc的大小,故原命题为假命题。
(2)因为ac2>bc2, 所以c≠0, 从而c2>0,故原命题为真命题。
(3)因为![]() 所以a2>ab ①
所以a2>ab ①
又![]() 所以ab>b2 ②
所以ab>b2 ②
综合①②得a2>ab>b2
故原命题为真命题.
(4)两个负实数,绝对值大的反而小.故原命题为真命题.
(5)因为![]() 所以
所以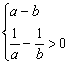
所以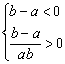 从而ab<0
从而ab<0
又因a>b 所以a>0,
b<0.
故原命题为真命题.
例2.已知f(x)=ax2-c且-4≤f(1)≤-1,-1≤f(2)≤5, 求f(3)的范围.
解:由题意可知:![]() ∴
∴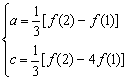
∴f(3)=9a-c=![]() f(2)-
f(2)-![]() f(1) ∴运算可知 -1≤f(3)≤20
f(1) ∴运算可知 -1≤f(3)≤20
错解:依题设有![]() ① 消元,得
① 消元,得![]() ②
②
∵f(3)=9a-c ∴-7≤f(3)≤26
错因:根源在于不等式组①与不等式组②并不等价,不等式组②扩大了不等式组①的解的范围,同向不等式在多次相加时要谨慎,一定要检查其同解性.
例3.设a,b是不相等的正数:A=![]() ,
G=
,
G=![]() ,
H=
,
H=![]() ,
Q=
,
Q=![]() , 试比较A、G、H、Q的大小.
, 试比较A、G、H、Q的大小.
解:由于a,b为不相等的正数.
所以:G-H=![]() -
-![]() =
=![]() -
-![]()
=![]() =
=![]()
=![]() >0
>0
从而 H<G
A-G=![]() -
-![]() =
=![]() =
=![]() >0
从而G<A
>0
从而G<A
Q-A=![]() -
-![]() =
=![]() -
-![]()
>![]() -
-![]() =0 从而A<Q
=0 从而A<Q
综上所述,当a, b为不相等的正实数时,H<G<A<Q.评述:本题直接比较G、H;A、G;Q、A的原因在于由特殊值可对四者排序,令a=1,
b=3则A=2, G=![]() ,H=
,H=![]() ,
Q=
,
Q=![]() ,这为我们解题指明了方向.
,这为我们解题指明了方向.
例4.设a, b∈N+ s
(1)求证:![]() 在
在![]() 与
与![]() 之间; (2)问
之间; (2)问![]() 与
与![]() 哪一个更接近
哪一个更接近![]() ?
?
证明:(1)由于(![]() -
-![]() )(
)(![]() -
-![]() )
)
=-![]() (*)
(*)
∵![]() a≠b
a≠b
所以(*)式的值小于0
从而![]() 在
在![]() 与
与![]() 之间
之间
解(2)由于![]() -
-![]() =
=![]()
![]() a-b
a-b
![]() =
=![]()
![]() a-b
a-b
∵![]() >
>![]() >
>![]()
∵![]()
![]() a-b>
a-b>![]()
![]() a-b
故而
a-b
故而![]() 更接近
更接近![]()
例5.船在流水中在甲地和乙地间来回驶一次平均速度和船在静水中的速度是否相等,为什么?
解:设甲、乙两地的距离为S,船在静水中的速度为u,水流速度为v(u>v>0)则船在甲、乙两地行驶的时间t为:
t=![]() +
+![]() =
=![]() 平均速度
平均速度![]() =
=![]() =
=![]()
∵![]() -u=
-u=![]() -u=
-u=![]() =
=![]() <0 ∴
<0 ∴![]() <u
<u
从而船在流水中来回一次的平均速度小于船在静水中的速度.
练习
1.若a,b,c为实数,判断下列命题的真假
(1)若a>b, 则ac2>bc2;(2)若a<b<0,则![]() <
<![]() ;
;
(3)若a<b<0,则![]() >
>![]() ;(4)若a<b<0,则
;(4)若a<b<0,则![]() <1;(5)若c>a>b>0,则
<1;(5)若c>a>b>0,则![]() >
>![]() .
.
2.设x,y∈R,判定下列两题中,命题甲与命题乙的充分必要条件.
(1)命题甲![]() 命题乙
命题乙![]() (2)命题甲
(2)命题甲![]() 命题乙
命题乙![]()
3.a∈R,试比较3(1+a2+a4)与(1+a+a2)2的大小.
4.a>1, m>n>0,比较am+![]() 和an+
和an+![]() 的大小.
的大小.
5.已知函数y=f(x), x∈R满足
(1)对x∈R,都有f(x)≥2;(2)对x1∈R,x2∈R, 都有f(x1+x2)≤f(x1)f(x2)
求证:对任意实数x1, x2,都有:lgf(x1+x2)≤lgf(x1)+lgf(x2)
参考答案
1.解(1)∵c2≥0,当c=0时ac2=bc2=0故原命题为假命题
(2)举特例-2<-1<0但-![]() >-1故原命题为假命题
>-1故原命题为假命题
(3)由于a<b<0 所以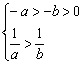 所以
所以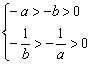 ∴
∴![]()
故原命题为假命题
(4)∵a<b<0 ∴a>b>0 ∴![]() <1 ∴
<1 ∴![]() <1故原命题为真命题.
<1故原命题为真命题.
(5)∵c>a>b>0 ∴![]() ∴c-b>c-a>0∴
∴c-b>c-a>0∴![]() >
>![]() >0
>0
又∵a>b>0 ∴![]() >
>![]() 故原命题为真命题.
故原命题为真命题.
2.解(1)当x>0,
y>0时,很明显x+y>0, xy>0
当xy>0时,x,y同号;又x+y>0,可知x, y同正,即x>0, y>0.
因此:命题甲是命题乙的充要条件.
(2)∵x>2>0,y>2>0∴x+y>4, xy>4
但是:![]()
![]()
![]()
反例如下:x=5, y=1, 这时x+y=6>4, xy=5>4, 但x>2, y<2
因此:命题甲是命题乙的充分但不必要条件.
3.解:3(1+a2+a4)(1+a+a2)2
=3+3a2+3a4-(1+a2+a4+2a+2a3+2a2)=2a4-2a3-2a+2
=2(a-1)2(a2+a+1)≥0 ∴3(1+a2+a4)≥(1+a+a2)2
4.解:∵(am+![]() )-(an+
)-(an+![]() )=(am-an)+(
)=(am-an)+(![]() )=
)=![]()
由a>1, m>n>0可知am>an,am+n>1
∴(am+![]() )-(an+
)-(an+![]() )>0即:am+
)>0即:am+![]() >an+
>an+![]()
5.证明:设x1∈R,x2∈R.
∵f(x1)f(x2)-[f(x1)+f(x2)]=f(x1)[![]() -1]+f(x2)[
-1]+f(x2)[![]() -1]
-1]
∵对任意x∈R
f(x)≥2 ∴![]() -1≥0
-1≥0 ![]() -1≥0∴f(x1)f(x2)≥f(x1)+f(x2)
-1≥0∴f(x1)f(x2)≥f(x1)+f(x2)
再由条件(2) f(x1+x2)≤f(x1)+f(x2)∴对任意实数x1∈R x2∈R有:
f(x1+x2)≤f(x1)·f(x2)∴lgf(x1+x2)≤lgf(x1)f(x2)=lgf(x1)+lgf(x2)
从而对任意实数x1∈R,x2∈R有:lgf(x1+x2)≤lgf(x1)+lgf(x2)
不等式综合能力测试
一、选择题:
1.设I=R,集合M={xlg(x+1)≤0},则![]() 等于( )
等于( )
A、(-∞,-1)∪(0,+∞) B、(-∞,0]
C、(-∞,-1)∪[0,+∞) D、(-∞,0)
2.若函数y=lg[1+![]() (1+log2x)]的值域为R+,则其定义域为( )
(1+log2x)]的值域为R+,则其定义域为( )
A、R+
B、(1,+∞) C、(![]() ,+∞)
D、(
,+∞)
D、(![]() ,1)
,1)
3.使方程cos2x+sinx=a有实数解的a的取值范围是( )
A、(-∞,![]()
![]() B、[-1,
B、[-1,![]() ]
C、[0,
]
C、[0,![]() ]
D、[-2,
]
D、[-2,![]() ]
]
4.已知函数:(1)
y=x+![]() (x≠0),
(2)y=cosx+
(x≠0),
(2)y=cosx+![]() (0<x<
(0<x<![]() ),
),
(3)y=![]() (x+8x+
(x+8x+![]() )(x>0),
(4) y=(1+cotx)(
)(x>0),
(4) y=(1+cotx)(![]() +2tgx)(0<x<
+2tgx)(0<x<![]() ).这四个函数中以4为最小值的个数为( )
).这四个函数中以4为最小值的个数为( )
A、0 B、1 C、2 D、3
5.如果a>b>c,则有( )
A、a>b>c B、a<b<c C、a-c>c-b D、a+b>b+c
6.不等式![]() ≥x+1的解集是( )
≥x+1的解集是( )
A、{x-1≤x≤1} B、{x0≤x≤1} C、{xx≤-1} D、{x-1≤x≤0)
二、填空题
7.已知a、b、c∈R+,且a+b+c=1,
则![]() 的最小值是____________.
的最小值是____________.
8.loga(1+a)与loga(1+![]() )
(a>0且a≠1)的大小关系是____________.
)
(a>0且a≠1)的大小关系是____________.
9.设x>0,
则函数y=![]() +x2,
当x=_______时,有最小值__________.
+x2,
当x=_______时,有最小值__________.
10.不等式lg(x2+2x+2)<1的解集是______________.
11.函数y=![]() +arcsin(2x-3)的定义域为___________.
+arcsin(2x-3)的定义域为___________.
12.不等式![]() x>
x>![]() 2-
2-![]() 的解集是___________.
的解集是___________.
三、解答题
13.解不等式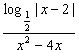 <0.
<0.
14.如果0<a<1,
0<b<1, 0<c<1, 试证:(1-a)b,
(1-b)c, (1-c)a不能同时大于![]() .
.
15.解不等式![]() +
+![]() >0.
>0.
16.已知a<1,
b<1, c<1, 求证:![]() <1.
<1.
17.若xy=100,
x≥![]() ,
y≥
,
y≥![]() ,
求lg(ylgx)的最大值和最小值.
,
求lg(ylgx)的最大值和最小值.
18.轮船航行的费用分为两部分,第一部分是轮船的折旧费或其它服务费用,每小时480元;第二部分为燃料费,它与速度的立方成正比.并且当速度为10公里/小时时,燃料费为每小时30元.问航行速度为多少时,才能使航行每公里的费用最小?并求出这个最小值,此时每小时的费用总和多少?
答案:
1.A 2.D 3.D 4.A 5.C 6.D
7.9
8.
loga(1+a)>loga(1+![]() )
9.
)
9.
![]()
10.
{x-4<x<2} 11.
[1, ![]() ]
12.
{xx<
]
12.
{xx<![]() }
}
13.
由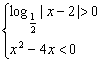 或
或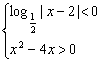
解得原不等式的解集为{xx<0或1<x<2或2<x<3或x>4}.
14.假设(1-a)b,
(1-b)c, (1-c)a同大于![]() ,∴
abc(1-a)(1-b)(1-c)>(
,∴
abc(1-a)(1-b)(1-c)>(![]() )3.....(1)
)3.....(1)
又
a(1-a)≤(![]() )2=
)2=![]() ,
即a(1-a)≤
,
即a(1-a)≤![]() ,同理b(1-b)≤
,同理b(1-b)≤![]() ,
c(1-c)≤
,
c(1-c)≤![]() ,∴
abc(1-a)(1-b)(1-c)≤(
,∴
abc(1-a)(1-b)(1-c)≤(![]() )3.......(2)
)3.......(2)
(1)与(2)矛盾,所以结论成立.
15.设x=tana
(-90°<a<90°),则![]() =sina,
=sina,
![]() =cos2a,原不等式化为sina+cos2a>0,
=cos2a,原不等式化为sina+cos2a>0,
即
2sin2a-sina-1<0,
∴ -![]() <sina<1.-
<sina<1.-![]() <a<
<a<![]() ,
∴
x=tana>-
,
∴
x=tana>-![]() .故
原不等式的解集是(-
.故
原不等式的解集是(-![]() ,+¥).
,+¥).
16.![]() <1Û
<1Û![]() <1Ûa2+b2+c2+a2b2c2<1+a2b2+b2c2+c2a2Û(1-a2)(1-b2)(1-c2)>0,即 原不等式成立.
<1Ûa2+b2+c2+a2b2c2<1+a2b2+b2c2+c2a2Û(1-a2)(1-b2)(1-c2)>0,即 原不等式成立.
17.设M=lg(ylgx)=lgx·lgy,∵
x≥![]() ,
y≥
,
y≥![]() ,
∴ lgx>0, lgy>0∴ M≤(
,
∴ lgx>0, lgy>0∴ M≤(![]() )2=(
)2=(![]() )2=1,
)2=1,
当x=y=10时等号成立,又 xy=100, ∴ lgx+lgy=2∴ M=-(lgx-1)2+1,
由x≥![]() ,
y≥
,
y≥![]() ,得lgx≥
,得lgx≥![]() ,
lgy≥
,
lgy≥![]() ,∴
lgx∈[
,∴
lgx∈[![]() ,
,
![]() ]
当lgx=
]
当lgx=![]() 或lgx=
或lgx=![]() 时,M有最小值
时,M有最小值![]() ,
,
故lg(ylgx)的最大值为1,最小值为![]() .
.
18.设每小时的费用总和为t元,航行速度为x公里/小时,∴t=kx3+480(x≥0),
由已知得103k=30得k=![]() ,
即t=
,
即t=![]() x3+480,
x3+480,
设每公里的航行费用为y元,得y=![]() (
(![]() x3+480)=
x3+480)=![]() x2+
x2+![]() +
+![]() ≥3
≥3![]() =36,当x=20时取等号,答(略).
=36,当x=20时取等号,答(略).