|
|
学科:数学 |
| 教学内容:参数方程、极坐标 |
一、考纲要求
1.理解参数方程的概念,了解某些常用参数方程中参数的几何意义或物理意义,掌握参数方 程与普通方程的互化方法.会根据所给出的参数,依据条件建立参数方程.
2.理解极坐标的概念.会正确进行点的极坐标与直角坐标的互化.会正确将极坐标方程化为 直角坐标方程,会根据所给条件建立直线、圆锥曲线的极坐标方程.不要求利用曲线的参数 方程或极坐标方程求两条曲线的交点.
二、知识结构
1.直线的参数方程
(1)标准式 过点Po(x0,y0),倾斜角为α的直线l(如图)的参数方程是
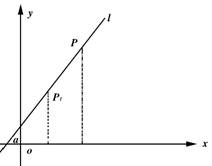
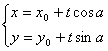 (t为参数)
(t为参数)
(2)一般式 过定点P0(x0,y0)斜率k=tgα=![]() 的直线的参数方程是
的直线的参数方程是
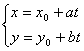 (t不参数) ②
(t不参数) ②
在一般式②中,参数t不具备标准式中t的几何意义,若a2+b2=1,②即为标准式,此时, | t|表示直线上动点P到定点P0的距离;若a2+b2≠1,则动点P到定点P0的距离是
![]() |t|.
|t|.
直线参数方程的应用 设过点P0(x0,y0),倾斜角为α的直线l的参数方程是
![]() (t为参数)
(t为参数)
若P1、P2是l上的两点,它们所对应的参数分别为t1,t2,则
(1)P1、P2两点的坐标分别是
(x0+t1cosα,y0+t1sinα)
(x0+t2cosα,y0+t2sinα);
(2)|P1P2|=|t1-t2|;
(3)线段P1P2的中点P所对应的参数为t,则
t=![]()
中点P到定点P0的距离|PP0|=|t|=|![]() |
|
(4)若P0为线段P1P2的中点,则
t1+t2=0.
2.圆锥曲线的参数方程
(1)圆 圆心在(a,b),半径为r的圆的参数方程是
![]() (
(![]() 是参数)
是参数)
φ是动半径所在的直线与x轴正向的夹角,![]() ∈[0,2π](见图)
∈[0,2π](见图)
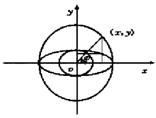
(2)椭圆 椭圆![]() =1(a>b>0)的参数方程是
=1(a>b>0)的参数方程是
![]() (
(![]() 为参数)
为参数)
椭圆 ![]() =1(a>b>0)的参数方程是
=1(a>b>0)的参数方程是
![]() (
(![]() 为参数)
为参数)
3.极坐标
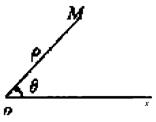
极坐标系 在平面内取一个定点O,从O引一条射线Ox,选定一个单位长度以及计算角度的正 方向(通常取逆时针方向为正方向),这样就建立了一个极坐标系,O点叫做极点,射线Ox叫 做极轴.
①极点;②极轴;③长度单位;④角度单位和它的正方向,构成了极坐标系的四要素,缺一 不可.
点的极坐标 设M点是平面内任意一点,用ρ表示线段OM的长度,θ表示射线Ox到OM的角度 ,那么ρ叫做M点的极径,θ叫做M点的极角,有序数对(ρ,θ)叫做M点的极坐标.(见图)
极坐标和直角坐标的互化
(1)互化的前提条件
①极坐标系中的极点与直角坐标系中的原点重合;
②极轴与x轴的正半轴重合
③两种坐标系中取相同的长度单位.
(2)互化公式
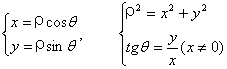
三、知识点、能力点提示
(一)曲线的参数方程,参数方程与普通方程的互化
例1 在圆x2+y2-4x-2y-20=0上求两点A和B,使它们到直线4x+3y+19=0的距离分别最短和最长.
解: 将圆的方程化为参数方程:
![]() (θ为参数)
(θ为参数)
则圆上点P坐标为(2+5cosθ,1+5sinθ),它到所给直线的距离为d=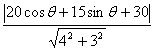 =|4cosθ+3sinθ +6|=5·|(
=|4cosθ+3sinθ +6|=5·|(![]() cosθ+
cosθ+![]() sinθ)+
sinθ)+![]() | =5|cos(φ-θ)+
| =5|cos(φ-θ)+ ![]() |,其中cosφ=
|,其中cosφ=![]() ,sinφ=
,sinφ=![]() .故当cos(φ-θ)=1,即φ=θ时 ,d最长,这时,点A坐标为(6,4);当cos(φ-θ)=-1,即θ=φ-π时,d最短,这时,点B坐标为(-2,2).
.故当cos(φ-θ)=1,即φ=θ时 ,d最长,这时,点A坐标为(6,4);当cos(φ-θ)=-1,即θ=φ-π时,d最短,这时,点B坐标为(-2,2).
(二)极坐标系,曲线的极坐标方程,极坐标和直角坐标的互化
说明 这部分内容自1986年以来每年都有一个小题,而且都以选择填空题出 现.
例2 极坐标方程表示的曲线C1∶ρ=f(θ),C2∶ρ=-f(π+θ)必定是( )
A.关于直线θ=![]() 对称
B. 关于极点对称
对称
B. 关于极点对称
C.关于极轴对称 D.同一曲线
解:因(ρ,θ)与(-ρ,π+θ)表示相同的点,
故选D.
(三)综合例题赏析
例3 椭圆![]() (Φ是参数)的两个焦点坐标是( )
(Φ是参数)的两个焦点坐标是( )
A.(-3,5),(-3,-3) B.(3,3),(3,-5)
C.(1,1),(-7,1) D.(7,-1),(-1,-1)
解:化为普通方程得![]() =1
=1
∴a2=25,b2=9,得c2=16,c=4.
∴F(x-3,y+1)=F(0,±4)
∴在xOy坐标系中,两焦点坐标是(3,3)和(3,-5).
应选B.
例4 参数方程
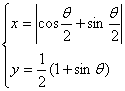 (0 <θ<2π)表示( )
(0 <θ<2π)表示( )
A.双曲线的一支,这支过点(1,![]() )
)
B.抛物线的一部分,这部分过(1,![]() )
)
C.双曲线的一支,这支过(-1,![]() )
)
D.抛物线的一部分,这部分过(-1,![]() )
)
解:由参数式得x2=1+sinθ=2y(x>0)
即y=![]() x2(x>0).
x2(x>0).
∴应选B.
例5 曲线的参数方程为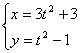 (0≤t≤5)则曲线是( )
(0≤t≤5)则曲线是( )
A.线段 B.双曲线的一支
C.圆弧 D.射线
解 消去t2得,x-2=3(y-1)是直线
又由0≤t≤5,得2≤x≤77,故为线段
应选A.
例6 下列参数方程(t为参数)与普通方程x2-y=0表示同 一曲线的方程是( )
A.![]() B.
B.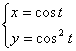
C.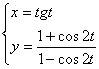 D.
D.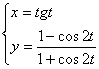
解:普通方程x2-y中的x∈R,y≥0,A.中x=|t|≥0,B. 中x=cost∈〔-1,1〕,故排除A.和B.
C.中y=![]() =ctg 2t=
=ctg 2t=![]() =
=![]() ,即x2y=1,故排除C.
,即x2y=1,故排除C.
∴应选D.
例7 曲线的极坐标方程ρ=4sinθ化 成直角坐标方程为( )
A.x2+(y+2)2=4 B.x2+(y-2)2=4
C.(x-2)2+y2=4 D.(x+2)2+y2=4
解:将ρ=![]() ,sinθ=
,sinθ=![]() 代入ρ=4sinθ,得
代入ρ=4sinθ,得
x2+y2=4y,即x2+(y-2)2=4.
∴应选B.
例8 极坐标ρ=cos(![]() -θ)表示的曲线是( )
-θ)表示的曲线是( )
A.双曲线 B.椭圆 C.抛物线 D.圆
解:原极坐标方程化为ρ=![]() (cosθ+sin θ);
(cosθ+sin θ);![]() ρ2=ρcosθ+ρsinθ,
ρ2=ρcosθ+ρsinθ,
∴普通方程为![]() (x2+y2)=x+y,表示圆.
(x2+y2)=x+y,表示圆.
应选D.
例9 在极坐标系中,与圆ρ=4sinθ相切 的条直线的方程是( )
A.ρsinθ=2 B.ρcos θ=2
C.ρcosθ=-2 D.ρcosθ=-4
解:如图.
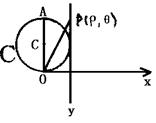
⊙C的极坐标方程为ρ=4sinθ,CO⊥OX,OA为直径,|OA|=4,l和圆相切,l 交极轴于B(2,0)点P(ρ,θ)为l上任意一点,则有
cosθ=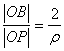 ,得ρcosθ=2,
,得ρcosθ=2,
∴应选B.
例10 极坐标方程4sin2θ=3表示曲线是 ( )
A.两条射线 B.两条相交直线
C.圆 D.抛物线
解:由4sin2θ=3,得4·![]() =3,即y2=3
x2,y=±
=3,即y2=3
x2,y=±![]() x,它表示两相交直线.
x,它表示两相交直线.
∴应选B.

【同步达纲练习】
(一)选择题
1.点P的直角坐标为(1,-![]() ),则点P的极坐标为( )
),则点P的极坐标为( )
A.(2,![]() )
B.(2,
)
B.(2,![]() )
C.(2,-
)
C.(2,-![]() )
D.(-2,-
)
D.(-2,-![]() )
)
2.直线:3x-4y-9=0与圆:![]() ,(θ为参数)的位置关系是( )
,(θ为参数)的位置关系是( )
A.相切 B.相离
C.直线过圆心 D.相交但直线不过圆心
3.若(x,y)与(ρ,θ)(ρ∈R)分别是点M的直角坐标和极坐标,t表示参数,则下列各组曲 线:①θ=![]() 和sinθ=
和sinθ=![]() ;②θ=
;②θ=![]() 和tgθ=
和tgθ=![]() ,③ρ2-9=0和ρ= 3;④
,③ρ2-9=0和ρ= 3;④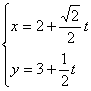 和
和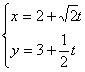 .
.
其中表示相同曲线的组数为( )
A.1 B.2
C.3 D.4
4.设M(ρ1,θ1),N(ρ2,θ2)两点的极坐标同时满足下列关系:ρ1+ρ2=0 ,θ1+θ2=0,则M,N两点位置关系是( )
A.重合 B.关于极点对称
C.关于直线θ=![]() D.关于极轴对称
D.关于极轴对称
5.实数x,y,θ满足x+yi=(cosθ+isinθ)(3cosθ+isinθ),当θ
变化时,点(x,y)的轨迹是( )
A.椭圆 B.双曲线 C.抛物线 D.圆
6.经过点M(1,5)且倾斜角为![]() 的直线,以定点M到动 点P的位移t为参数的参数方程是( )
的直线,以定点M到动 点P的位移t为参数的参数方程是( )
A.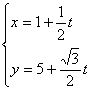 B.
B.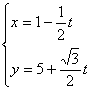
C.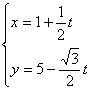 D.
D.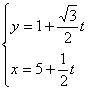
7.将参数方程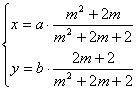 (m是参数,ab≠0)化为普通方程是( )
(m是参数,ab≠0)化为普通方程是( )
A.![]() =1(x≠a)
B.
=1(x≠a)
B.![]() =1(x≠-a )
=1(x≠-a )
C. ![]() =1(x≠a)
D.
=1(x≠a)
D. ![]() =1(x≠-a )
=1(x≠-a )
8.把极坐标方程ρ=2sin(![]() +θ)化为直角坐标方程为( )
+θ)化为直角坐标方程为( )
A.(x-![]() )2+(y-
)2+(y-![]() )2=1
B.y2=2(x-
)2=1
B.y2=2(x-![]() )
)
C.(x-![]() )(y-
)(y-![]() )=0 D.
)=0 D.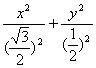 =1
=1
9.参数方程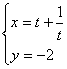 (t为参数)所表示的曲线是 ( )
(t为参数)所表示的曲线是 ( )
A.一条射线 B.两条射线
C.一条直线 D.两条直线
10.双曲线![]() (θ为参数)的渐近线方程为( )
(θ为参数)的渐近线方程为( )
A.y-1=±![]() (x+2)
B.y=±
(x+2)
B.y=±![]() x
x
C.y-1=±2(x+2) D.y+1=±2(x-2)
11.直线![]() (t为参数)与圆
(t为参数)与圆![]() (θ为参数)相切,则直线的倾斜角为( )
(θ为参数)相切,则直线的倾斜角为( )
A.![]() 或
或![]() B.
B. ![]() 或
或![]() C.
C. ![]() 或
或![]() D.-
D.- ![]() 或-
或-![]()
12.已知曲线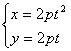 (t为参数)上的点M,N对应的参数分别为t1,t2,且t1+t2=0,那么M,N间的距离为( )
(t为参数)上的点M,N对应的参数分别为t1,t2,且t1+t2=0,那么M,N间的距离为( )
A.2p(t1+t2) B.2p(t21+t22)
C.│2p(t1-t2)│ D.2p(t1-t2)2
13.若点P(x,y)在单位圆上以角速度ω按逆时针方向运动,点M(-2xy,y2-x2)也在单位 圆上运动,其运动规律是( )
A.角速度ω,顺时针方向 B.角速度ω,逆时针方向
C.角速度2ω,顺时针方向 D.角速度2ω,逆时针方向
14.已知过曲线![]() (θ为参数,且0≤θ≤π)上一点P 与原点O的直线PO的倾斜角为
(θ为参数,且0≤θ≤π)上一点P 与原点O的直线PO的倾斜角为![]() ,则P点坐标是( )
,则P点坐标是( )
A.(3,4)
B.(![]() ,2
,2![]() )
)
C.(-3,-4)
D.(![]() ,
,![]() )
)
15.直线ρ=![]() 与直线l关于 直线θ=
与直线l关于 直线θ=![]() (ρ∈R)对称,则l的方程是( )
(ρ∈R)对称,则l的方程是( )
A.ρ=![]() B.ρ=
B.ρ=![]()
C.ρ=![]() D.ρ=
D.ρ=![]()
(二)填空题
16.双曲线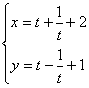 的中心坐标是
.
的中心坐标是
.
17.参数方程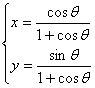 (θ为参数)化成普通方程为
.
(θ为参数)化成普通方程为
.
18.极坐标方程ρcos(θ-![]() )=1的直角坐标方程是
.
)=1的直角坐标方程是
.
19.抛物线y2=2px(p>0)的一条过焦点的弦被焦点分成m、n长的两段,则![]() =
.
=
.
(三)解答题
20.设椭圆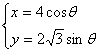 (θ为参数) 上一点P,若点P在第一象限,且∠xOP=
(θ为参数) 上一点P,若点P在第一象限,且∠xOP=![]() ,求点P的坐 标.
,求点P的坐 标.
21.曲线C的方程为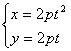 (p>0,t为参数),当t∈[-1,2]时 ,曲线C的端点为A,B,设F是曲线C的焦点,且S△AFB=14,求P的值.
(p>0,t为参数),当t∈[-1,2]时 ,曲线C的端点为A,B,设F是曲线C的焦点,且S△AFB=14,求P的值.
22.已知过点P(1,-2),倾斜角为![]() 的直线l和抛物线x2=y+m
的直线l和抛物线x2=y+m
(1)m取何值时,直线l和抛物线交于两点?
(2)m取何值时,直线l被抛物线截下的线段长为![]() .
.
23.如果椭圆的右焦点和右顶点的分别是双曲线![]() (θ 为参数)的左焦点和左顶点,且焦点到相应的准线的距离为
(θ 为参数)的左焦点和左顶点,且焦点到相应的准线的距离为![]() ,求这椭圆上的点到双曲线渐近线的最短距离.
,求这椭圆上的点到双曲线渐近线的最短距离.
24.A,B为椭圆![]() =1,(a>b>0) 上的两点,且OA⊥OB,求△AOB的面积的最大值和最小值.
=1,(a>b>0) 上的两点,且OA⊥OB,求△AOB的面积的最大值和最小值.
25.坐标平面上有动点P(cos2t+sin2t,-cos2t+sin2t),Q(![]() cost-sint,cost+
cost-sint,cost+![]() sint),t∈[0,π],当t变化时:
sint),t∈[0,π],当t变化时:
(1)求P,Q两动点的轨迹;
(2)当|PQ|=![]() 时,求t的值.
时,求t的值.

参考答案
【同步达纲练习】
(一)1.C 2.D 3.C 4.C 5.D 6.A 7.A 8.A 9.B 10.C 11.A 12.C 13.C 14.D 15.D
(二)16.(2,-1);17.y2=-2(x-![]() ),(x≤
),(x≤![]() );18.
);18.![]() x+y-z=0;19.
x+y-z=0;19.![]()
(三)20.(![]() ,
,![]() );21.
);21.![]() ;
;
22.(1)m>![]() ,(2)m=3;23.
,(2)m=3;23.![]() (27-3
(27-3![]() );24.Smax=
);24.Smax=![]() ,smin=
,smin=![]() ;
;
25.(1)P点轨迹为圆x2+y2=2,Q点的轨迹为半径圆x2+y2=4(y≥0),(2)t=![]() 或t=
或t=![]() .
.
