秘密★启用前
春季普通高中毕业考试数学试题
数 学
本试卷分选择题)和非选择题两部分,共6页,满分为100分,考试时间100分钟。
注意事项:
1.答卷前,考生务在答题卡上用黑色字迹的钢笔或签字笔填写自己的准考证号、姓名;填写考场试室号、座位号,再用2B铅笔把对应两号码的标号涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回。
第一部分 选择题 (共60分)
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)
S=4![]() R2
R2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是p, ![]()
那么n次独立重复试验中恰好发生k次的概 其中R表示球的半径
率![]()
一、选择题:本大题共20小题,每小题3分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)设全集U={a,b,c,d,},集合M={a,c,d},N={b, d},则(![]() UM)∩N=
UM)∩N=
(A) { b } (B) { d }
(C) { a, c } (D) {b, d }
(2)已知f(x)在区间(0,5)上是减函数,则下列不等式成立的是
(A)f(![]() )< f(
)< f(![]() ) (B)f(
) (B)f(![]() )< f(
)< f(![]() )
)
(C)f(![]() )< f(π)
(D)f(
)< f(π)
(D)f(![]() )< f(2)
)< f(2)
(3)已知向量![]() 的夹角大小为
的夹角大小为
(A)0° (B)45°
(C)90° (D)180°
(4)![]() 的展开式中,x2的系数是
的展开式中,x2的系数是
(A)-5 (B)5
(C)-10 (D)10
(5)已知![]()
(A)![]() (B)-
(B)-![]()
(C)![]() (D)-
(D)-![]()
(6)不等式![]()
![]() 的解集为
的解集为
(A){x ![]() ≤x≤2}
(B){x
≤x≤2}
(B){x ![]() ≤x<2}
≤x<2}
(C){x x>2或x≤![]() } (D){x x<2}
} (D){x x<2}
(7)双曲线![]() -
-![]() 的离心率为
的离心率为
(A)![]() (B)2
(C)
(B)2
(C)![]() (D)
(D)![]()
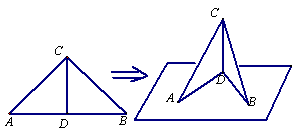 (8)如图Rt△
(8)如图Rt△![]() 中,
中,![]() ,
,
![]() ,沿
,沿![]() 将△
将△![]() 折成
折成![]() 的二面
的二面
角A—CD—B,则折叠后点![]() 到平面
到平面![]() 的距离是
的距离是
(A)1 (B)![]() (C)
(C)![]() (D)2
(D)2
(9)已知数列{an}的前n项和Sn=![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)命题甲“![]() ”,命题乙“
”,命题乙“![]() ”,那么甲是乙的
”,那么甲是乙的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分又不必要条件
(11)若函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则
(A)![]()
![]() (B)
(B)![]()
![]()
(C)![]()
![]() (D)
(D)![]()
![]()
(12)下列命题中,为真命题的是
(A)若![]() ,则
,则![]() (B)若
(B)若![]() ,则
,则![]()
(C)若![]() ,则
,则![]() (D)若
(D)若![]() ,则
,则![]()
(13)在![]() 则这个三角形一定是
则这个三角形一定是
(A)锐角三角形 (B)钝角三角形
(C)直角三角形 (D等腰三角形
(14)若函数![]()
![]() (
(![]() ),则
),则![]()
(A)在(![]() )内单调递增 (B)在(
)内单调递增 (B)在(![]() )内单调递减
)内单调递减
(C)在(![]() )内单调递增 (D)在(
)内单调递增 (D)在(![]() )内单调递减
)内单调递减
(15)在空间中,a、b、c是两两不重合的三条直线,![]() 、
、![]() 、
、![]() 是两两不重合的三个平面,下列命题正确的是
是两两不重合的三个平面,下列命题正确的是
(A)若两直线a、b分别与平面![]() 平行,则a//b
平行,则a//b
(B)若直线a与平面![]() 内的一条直线b平行,则
内的一条直线b平行,则![]()
(C)若直线a与平面![]() 内的两条直线b、c都垂直,则
内的两条直线b、c都垂直,则![]()
(D)若平面![]() 内的一条直线a垂直平面
内的一条直线a垂直平面![]() 则
则![]()
(16)某完全中学初一至高三共6个年级,全校学生总人数为1926名,其中初一年级有342人,现采用按年级分层抽样的方法从该校所有学生中抽取一个容量为107人的样本进行学习兴趣调查,则从初一年级应抽取
(A)17人 (B)18人 (C)19人 (D)20人
(17)一道竞赛题,甲同学解出它的概率为![]() ,乙同学解出它的概率为
,乙同学解出它的概率为![]() ,丙同学解出它的概率为
,丙同学解出它的概率为![]() ,则独立解答此题时,三人中只有一人解出的概率为
,则独立解答此题时,三人中只有一人解出的概率为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)1
(D)1
(18)函数![]() 在区间(0,6)上的最大值是
在区间(0,6)上的最大值是
(A)![]() (B)
(B)![]() (C)12 (D)9
(C)12 (D)9
(19)若直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() ,则实数a的值为
,则实数a的值为
(A)–1或![]() (B)1或3 (C)–2或6 (D)0或4
(B)1或3 (C)–2或6 (D)0或4
(20)已知甲、乙两地的公路线长400千米,用10辆汽车从甲地向乙地运送一批物资,假设汽车以![]() 千米/小时的速度直达乙地,为了某种需要,两汽车间距不得小于
千米/小时的速度直达乙地,为了某种需要,两汽车间距不得小于![]() 千米(汽车车身长度忽略不计),则这批物资全部到达乙地的最短时间是
千米(汽车车身长度忽略不计),则这批物资全部到达乙地的最短时间是
(A)10小时 (B)12小时 (C)![]() 小时 (D)24小时
小时 (D)24小时
第二部分 非选择题 (共40分)
二.填空题:本大题共4小题,每小题3分,共12分.把答案填在题中横线上.
(21)正方体的棱长为1,它的顶点都在同一个球面上,那么这个球的表面积为 .
(22)若直线![]() 与直线
与直线![]() 平行,则实数
平行,则实数![]() 等于 .
等于 .
(23)已知函数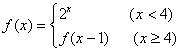 ,那么
,那么![]() 的值为
.
的值为
.
(24)一个口袋内有4个不同的红球,6个不同的白球,若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于8分的取法有_____________种 (用数字作答).
三.解答题:本大题共4小题,共28分.解答应写出文字说明、证明过程或演算步骤.
(25)(本小题满分6分)
已知函数![]() x
x![]() R.
R.
求![]() 的最大值,并求使
的最大值,并求使![]() 取得最大值时x的集合.
取得最大值时x的集合.
(26)(本小题满分6分)
某电影院大厅共有座位30排,第10排有座位38个,且从第二排起每排比前一排多2个座位,问这个大厅共有多少个座位?
(27)(本小题满分7分)
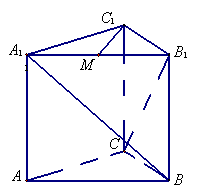 如图,直三棱柱
如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() , M是A1B1的中点.
, M是A1B1的中点.
(I) 求证C1M^平面![]() ;
;
(II) 求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
(28)(本小题满分9分)
已知向量![]() =(x,
=(x,![]() ),
),![]() =(1,0),且(
=(1,0),且(![]() +
+![]()
![]() )
)![]() (
(![]() –
–![]()
![]() ).
).
(I) 求点Q(x,y)的轨迹C的方程;
(II)设曲线C与直线![]() 相交于不同的两点M、N,又点A(0,-1),当
相交于不同的两点M、N,又点A(0,-1),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
春季普通高中毕业考试
数学试题参考答案及评分标准
一、选择题:本大题共20小题,每小题3分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)A (2)A (3)C (4)C (5)B (6)B (7)D
(8)C (9)A (10)D (11)B (12)A (13)B (14)D
(15)D (16)C (17)B (18)A (19)D (20)B
二、填空题:本大题共4小题,每小题3分,共12分,把答案填在题中横线上.
(21)![]() ; (22)
; (22)![]() ; (23)8; (24)66.
; (23)8; (24)66.
三、解答题:本大题共4小题,共28分.解答应写出文字说明、证明过程或演算步骤.
(25)解:∵![]()
=![]() ,
,
![]() .
.
∴ f(x)取到最大值为1. …… 3分
当 ![]() ,
,![]() Z时,
Z时,
![]() ,
,![]() Z,f(x)取到最大值为1.
Z,f(x)取到最大值为1.
∴ f(x)取到最大值时的x的集合为{![]()
![]() ,
,![]() Z }.
……6分
Z }.
……6分
(26)解:设该大厅第n排有![]() 个座位,
个座位,
则数列{![]() }是一个公差
}是一个公差![]() ,项数为30的等差数列,且
,项数为30的等差数列,且![]() =30;
=30;
∵![]() ,∴
,∴![]() ,
,
于是![]() ;
…… 3分
;
…… 3分
∴![]() .
…… 5分
.
…… 5分
答:该大厅一共有1470个座位. …… 6分
(27)解法一:(I)∵直三棱柱![]() ,
,
∴![]()
![]()
![]()
![]() , ∴
, ∴ ![]() ,
,
∵![]() , M是A1B1的中点, ∴
, M是A1B1的中点, ∴ ![]() .
.
 又
又![]()
![]() ∴ C1M^平面
∴ C1M^平面![]() . …… 3分
. …… 3分
(II)设![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,
,
连接![]() ,∴
,∴![]() ∥
∥![]() ,
,
连接![]() ,∴
,∴![]() ∥
∥![]() ,
,
∴![]() 是异面直线
是异面直线![]() 与
与![]() 所成角或其补角;
所成角或其补角;
-------------------------------------------------------5分
设点![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() ,
,
在Rt△![]() 中,
中,![]() ,
,
在△![]() 中,
中,![]() ,
,![]() ,
,
∴![]()
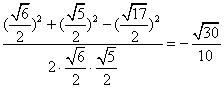 .
.
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
…… 7分
.
…… 7分
 解法二:(I)如图 以C为原点,
解法二:(I)如图 以C为原点,![]() 、
、![]() 、
、![]() 为坐标轴建立空间直角坐标系,
为坐标轴建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∵![]()
![]() =
=![]()
![]() =
=![]()
∴![]()
![]() .
.
同理![]() ⊥
⊥![]()
∴ C1M^平面![]() ……3分
……3分
(II) ∵![]() ,
,![]() ,
,
![]() ∴
∴![]() ,
,![]()
∴![]()
![]() ;
;![]() ,
,![]()
cos<![]() >=
>=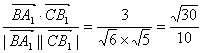 .
.
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
…… 7分
.
…… 7分
(28)解:(I)![]() +
+![]()
![]() =(x,
=(x,![]() )+
)+![]() (1,0)=(x+
(1,0)=(x+![]() ,
,![]() y)
y)
![]() –
–![]()
![]() =(x,
=(x,![]() )-
)-![]() (1,0)=(x-
(1,0)=(x-![]() ,
,![]() y)
y)
![]() (
(![]() +
+![]()
![]() )
)![]() (
(![]() -
-![]()
![]() )
)
![]() (
(![]() +
+![]()
![]() )·(
)·(![]() -
-![]()
![]() )=0
)=0
![]() (x+
(x+![]() )( x-
)( x-![]() )+
)+![]() y·
y·![]() y=0 得
y=0 得![]()
![]() Q点的轨迹C的方程为
Q点的轨迹C的方程为 ![]() .
……3分
.
……3分
(II)由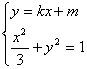 得
得 ![]()
由于直线与椭圆有两个交点,![]() 即
即 ![]() ① ……4分
① ……4分
(1)
当![]() ,设P为弦MN的中点,
,设P为弦MN的中点,
![]() 从而
从而![]()
![]() 又
又![]() ,则
,则
![]() 即
即 ![]() ② ……6分
② ……6分
把②代入①得 ![]() ,解得
,解得 ![]() ;
;
由②得 ![]() ,解得
,解得![]() .
.
故所求![]() 的取范围是(
的取范围是(![]() ,2).
…… 7分
,2).
…… 7分
(2)当![]() 时,
时,![]() ,
,![]() ,解得
,解得![]()
故所求![]() 的取范围是(
的取范围是(![]() ,1).
…… 8分
,1).
…… 8分
∴当![]() 时,
时, ![]() 的取值范围是(
的取值范围是(![]() ,2),当
,2),当![]() 时,
时, ![]() 的取值范围是(
的取值范围是(![]() ,1).
,1).
……9分