高三数学同步测试（3）

高中学生学科素质训练

　

高三数学同步测试（3）

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.

第Ⅰ卷（选择题 共60分）

参考公式：

如果事件A、B互斥，那么　　　　　　　　 球的表面积公式

P（A+B）=P（A）+P（B）　　　　　　　  S=4πR²

如果事件A、B相互独立，那么　　　　　　 其中R表示球的半径

P（A·B）=P（A）·P（B）　　　　　　球的体积公式

如果事件A在一次试验中发生的概率是P.　

那么n次独立重复试验中恰好发生k次的概　

率　　　　　　　　　　　　　　　　　　 其中R表示球的半径

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有

一项是符合题目要求的.

1．设集合，，是从集合到集合的映射，则在映射下，象的原象有　　　　　　　　　　　  　　　　　　　　　　　　　　　（　　）

A．1个　　　　　　　　　B．2个　　 　　　　　C．3个 　　　　　　　　　 D．4个

2. 若3个空汽水瓶可以换一瓶汽水，现有10个空汽水瓶，若不再交钱，最多可以喝汽水的瓶数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

　　　 A. 3　　　　　　  B. 4　　　　　　　　　 C. 5　　　　 　　　　　 D. 6

3．函数y=sin2x的图象按向量a平移后，所得函数的解析式是y=cos2x+1,则a等于（　　）

　 　A.  ( ,1)　 　　　　B.　(－ ,1) 　　　　C. (－ ,1)　　　　　 D.　(,1)

 

4. 已知等比数列的各项均为正数，公比Q=，则P与Q

的大小关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A.  P>Q　　　　　 B. P<Q　　　　  C.P=Q　　　　  　　D.无法确定

5．方程在上的解的个数是　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A. 4　　　　  　　　　B.3　　　　　  　　 C. 2　　　　  　　　　 D.1

6. 已知平面平面，直线，点，平面间的距离为8，则在内到点的距离为10，且到直线的距离为9的点的轨迹是　　　　　　　　　　　　　　　　　　　（　　）

　　　 A.一个圆　　　　　　　B.　两条直线　　　　　C. 四个点　　　　 D.　两个点

7．设，动点P到轴的距离为，则满足点P的轨迹方程是和的一个条件是　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　（　　）

　　　 A. 　　　　　　　　　 B.

　　　 C.　　　　　　　　　　D.

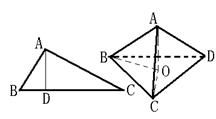
8．在⊿ABC中，AB⊥AC、AD⊥BC，D是垂足，则（射影定理）.类似有命题：三棱锥A-BCD（图2）中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在⊿BCD内，则.上述命题是　　　　　　　　　　　 （　　）

A.　　   真命题

B.　　   假命题

C.　　   增加AB⊥AC的条件才是真命题　　　

D.　　  增加三棱锥A-BCD是正三棱锥的

条件才是真命题

　　

9．圆C切y轴于点M且过抛物线与x轴的两个交点，O为原点，则OM的长是　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 （ 　 ）

　　A．4　　　　　　　　　　　　B．　　　　　　　　　　 C．　　　　　　　　　 D．2

10．甲船在千岛湖B岛的正南A处，AB = 3km. 甲船以8 km / h的速度向正北方向航行，同时乙船自B岛出发以12 km/ h的速度向北偏东60°的方向驶去，则行驶15分钟，两船之间的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　（ 　 ）

　 A.  km.　　　　B.  km.　　　　　C. km.　　　　　　D. km.

11．若是R上的减函数，且的图象过点和，则不等式的解集是　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A. 　　　　　　　B.　 　　　　 C.　　　　　 D.　

12. 我们用记号来表示复数cosq +isinq，即 (其中e= 2.71828…是自然对数的底数，q 的单位是弧度)．则：① ；　　 ② ； 　　　③ ． 其中正确的式子代号为　　　　　　　　　　　　　　　　  　　（　　）

A．①　　　　　  B．①②  　　　　 C．①③　 　　　　 D．②③

第Ⅱ卷（非选择题　共90分）

二、填空题：本大题共4小题，每小题4分，共16分.答案填在题中横线上.

13．若P为抛物线上任意一点，以P为圆心且与轴相切的圆必过定点M，则点M的坐标是__________________.

14．已知数列的通项公式为，又，则=__________.

 15．一个公司有N个员工，下设一些部门，现采用分层抽样方法从全体员工中抽取一个容量为n的样本 (N是n的倍数)．已知某部门被抽取了m个员工，那么这一部门的员工数是　　　　　　　　　  ．

 16．一次化学实验中需要用天平称出20g氧化铜粉末, 某同学发现自己所用的天平是不准的(其两臂不等长)，因此, 他采用了下列操作方法：选10g的法码放入左盘, 置氧化铜粉末于右盘使之平衡，取出氧化铜粉末, 然后又将10g法码放于右盘, 置氧化铜粉末于左盘, 平衡后再取出.  他这样称两次得到的氧化铜粉末之和应该　　　　　  20g. (选用“大于”，“小于”，“等于”，“不小于”，或“不大于”填空 )

三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.

17．（本小题满分10分）

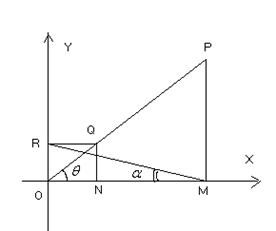
 如图，长为3的线段OP绕点O 旋转，设，Q　是OP上一点，且，过点P，Q向坐标轴作垂线，垂足为M，N，R，记.

(I) 求函数的解析式;

(II) 求的最大值，并求出相应的.

注意：考生在（18甲）、（18乙）两题中选一题作答，如果两题都答，只以（18甲）计分.

18．（本小题满分12分）

（甲）已知圆锥的侧面展开图是一个半圆，它被过底面中心O₁且平行于母线AB的平面所截，若截面与圆锥侧面的交线是焦参数（焦点到准线的距离）

为p的抛物线.

（I）求圆锥的母线与底面所成的角；

（II）求圆锥的全面积．

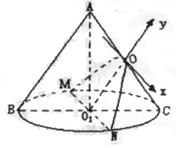
(乙) 已知：如图，直三棱柱ABC—A₁B₁C₁中，AC⊥BC，AC=BC=CC₁，M、N分别为A₁B、B₁C₁的中点.

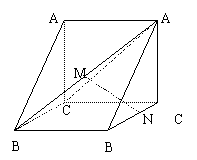（Ⅰ）求证：MN//平面ACC₁A₁；

（Ⅱ）求证：MN⊥平面A₁BC；

（Ⅲ）求二面角A—A₁B—C的大小.

19．（本小题满分12分）

某次国际网球邀请赛共有128位选手参加，比赛采用单淘汰制，即每轮淘汰一半的选手，剩下一半的选手进入下一轮. 在第1轮被淘汰的每位选手可获得出场费1万元，在第2轮被淘汰的选手可获得2万元，在第k轮被淘汰的选手可获得2 ^{k – 1} 万元，而冠军则可获得128万元.

（I）求本次网球邀请赛共需出场费多少万元？

（II）设网球场有3000个坐位，第一轮比赛门票价格为a元( a为整数)，第二轮比赛门票价格为a + 50元，第k轮比赛门票价格为a + 50(k – 1 )元. 假设每场比赛均满座，且每张门票可观看一轮的所有比赛，则要使本次邀请赛不亏本，第一轮门票价格a应该如何确定？

　　　　　　　　　　　　　　

20．（本小题满分12分）

　　如右图是在竖直平面内的一个“通道游戏”，图中竖直线段和斜线段都表示通道，并且在交点处相通，若竖直线段有一条的为第一层，有二条的为第二层，依次类推，现有一颗小弹子从第1层的通道里向下运动。求：

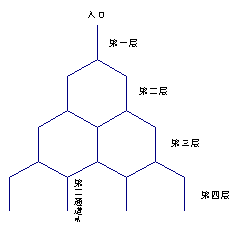（I）该小弹子落入第4层第2个竖直通道

的概率（从左向右数）；

（II）猜想落入第n+1层的第m个通道里的概率。

（III）该小弹子落入第层第个竖直通道的

　 路径数与该小弹子落入第层第个竖直通

 道的路径数之和等于什么？

[假设在交点处小弹子向左或向右是等可能的]．

21．（本小题满分14分）

　　　已知动点与双曲线的两个焦点、的距离之和为定值，且

的最小值为．

（I）求动点的轨迹方程；

（II）若已知，、在动点的轨迹上且，求实数的取值范围．

22．（本小题满分14分）

　 已知函数在区间[0，1]单调递增，在区间单调递减，

　　　 （I）求a的值；

　　　 （II）若点的图象上，求证点A关于直线的对称点B也在函数的图象上；

　　　 （III）是否存在实数b，使得函数的图象与函数的图象恰有3个交点，若存在，请求出实数b的值；若不存在，试说明理由.

高中学生学科素质训练

　

高三数学同步测试（3）

一、选择题

1.C　2.C  3.A　4.A　5.D  6.C　7.B　8.A  9.D  10.B　11.D　12.C

二、填空题

13． 　14． 　15．　 16. 大于  

三、解答题

17． （I）由图得　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

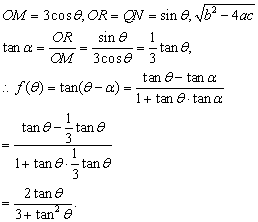
　　　　　　　　　　　　　　　　 ………6 分

（II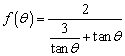）.　　………8分

当且仅当即时，最小值为2.

所以当时，最大，值为.

　　　　　　　　　　　　　　　 ……………12分

18．（甲小题）

　　 （I）设圆锥的底面半径为R，母线长为l，

由题意得：,　　　　　　　　　　 

即,　………4分所以母线和底面所成的角为　 ………6分

（II）设截面与圆锥侧面的交线为MON，其中O为截面与AC的交点，则OO₁//AB且　　 ………8分

在截面MON内，以OO₁所在有向直线为y轴，O为原点，建立坐标系，则O为抛物的顶点，所以抛物线方程为x²=－2py，点N的坐标为（R，－R），代入方程得

R²=－2p（－R），得R=2p，l=2R=4p.

∴圆锥的全面积为.　　 ………12分

18（乙小题）

（Ⅰ）连AC₁，AB₁. 由直三棱柱的性质，得AA₁⊥平面A₁B₁C₁，

∴AA₁⊥A₁B₁，则四边形ABB₁A₁为矩形.　　　　　　　　　 ……………………2分

由矩形性质得，AB₁过A₁B的中点M.

在△AB₁C₁中，由中位线性质，得MN//AC₁.

又AC₁平面ACC₁A₁，MN平面ACC₁A₁，

∴MN//平面ACC₁A₁.　　　　　　　　　 　　　　　 ……… …………4分

（Ⅱ）BC⊥平面ACC₁A₁，AC₁平面ACC₁A₁，

　　　∴BC⊥AC₁ 在正方形ACC₁A₁中，A₁C⊥AC₁

　　　又BC∩A₁C=C，∴AC₁⊥平面A₁BC.　　　　　　　  ………………………7分

　　　由MN//AC₁，∴MN⊥平面A₁BC.　　　　　　　　　　 ……………………8分

（Ⅲ）作CE⊥AB于E.

∵平面ABC⊥平面ABB₁A₁，∴CE⊥平面ABB₁A_{1 。}

 作EF⊥A₁B于F，连FC.　　由三垂线定理得A₁B⊥CF.

 ∠EFC为二面角A—A₁B—C的平面角　　　　　　　  …………………10分

令BC=2，在等腰Rt△ABC中，可求出.

在Rt△A₁BC中，由BC=2，A₁C=2，求出A₁B=2.

　　　　 由FC·A₁B=BC·A₁C, 求出

　　　　 故　 ∠EFC=60°.　　　　　　　　　　　　　　　　 …………………12分

19. （I）设奖金总数为W万元.则有

W = 64´1 + 32´2 + 16´2² + 8´2³ + 4´2⁴ + 2´2⁵ + 1´2⁶ + 2⁷

= 7´2⁶ + 2⁷ = 9´2⁶ (万元).　　　　　　　　　　　　　　　　　　  ……………4分　　　　　　　　　　　　　　　　 

　 (II) 设门票收入为y元，则

　 y = 3000[a + ( a + 50 ) + ( a + 100 ) + (a +150) + ( a + 200 ) + ( a +250) + ( a +300 ) ]

　　= 3000( 7a +1050 ) 　　　　　　　　　　　　　　　　　　　……………8分

比赛不亏本，则3000[7a + 1050] ³ 90000´2⁶ .

解得 a ³ 124.3　　　　　　　　　　　　　　　　　　　 　　　 ……………10分

故要使邀请赛不亏本，第一轮价格至少要定为125元.　　　　　  ……………12分

20．（I）∵在交点处小弹子向左或向右是等可能的，

∴小弹子落入第4层第1个竖直通道的路径只有1条，落入第4层第2个竖直通道的路径有3条，第3个有3条，第4个有1条，∴所求概率P= = .

……………4分

（II）利用杨辉三角的特点可猜想，所求的概率P= =.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……………8分

（III） ，即该小弹子落入第层第个竖直通道的路径数与该小弹子落入第层第个竖直通道的路径数之和等于该小弹子落入第层第个竖直通道的路径数.　　　　　　　　　　　　　　　　　　　　　　　　　　  ……………12分

21． (I)由题意，　　　　　　　　　　　　　　　　　　　　 ……………2分

设（），由余弦定理, 得

．

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……………4分

又·，　　　　　　　　　  ……………6分

当且仅当时，· 取最大值，

此时取最小值，令，

解得，，∴，故所求的轨迹方程为.　　 ……8分

（II）设，，则由，可得，

故.　　　　　　　　　　　　　　　 …………………10分

∵、在动点的轨迹上，故且，

消去可得，解得，　　　…………12分

又，∴，解得，

故实数的取值范围是．　　　　　　　　　　　　  ………………………14分

22．（I）由函数单调递增，在区间单调递减，

　　　　　　  ……………………………2分

　　　　　　　　　　　　　 …………………………4分

（II）点……6分

……………………………………………………8分

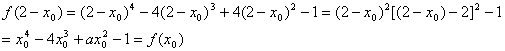
∴A关于直线x=1的对称点B也在函数f（x）的图象上.　………………………9分

（III）函数的图象与函数f（x）的图象恰有3个交点，等价于方程

个不等实根.　　 ……………………………10分

,

是其中一个根,

有两个非零不等实根.　　　　…………………12分

.　　　　　　 …………………………14分