高中学生学科素质训练
高三数学同步测试(4)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P. ![]()
那么n次独立重复试验中恰好发生k次的概
率 其中R表示球的半径
![]()
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.设P、Q是两个非空集合,定义P*Q={(a,b)a∈P,b∈Q},若P={0,1,2},Q={1,2,3,4},则P*Q中元素的个数是 ( )
A.4个 B.7个 C.12个 D.16个
2.某天清晨,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常,但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了. 下面大致能上反映出小鹏这一天(0时—24时)体温的变化情况的图是 ( )
 |
A B C D
3.一个容量为20的样本数据,分组后,组距与频数如下:
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
则样本在![]() 上的频数为 ( )
上的频数为 ( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
4.表示如图中阴影部分所示平面区域的不等式组是 ( )
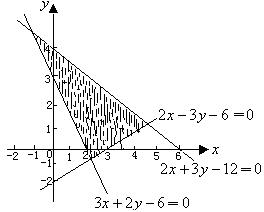 A.
A.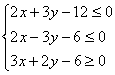
B.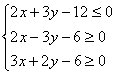
C.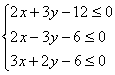
D.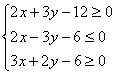
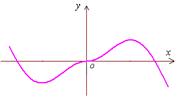
5.函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的解析式可能是 ( )
的解析式可能是 ( )
 A.
A.![]()
B.![]()
C.![]()
D.![]()
6. 已知向量a=![]() b=
b=![]() a与b的夹角为
a与b的夹角为![]() ,则直线
,则直线![]() 与圆
与圆![]() 的位置关系是 ( )
的位置关系是 ( )
A. 相切 B. 相交
C. 相离
D. 随![]() 的值而变化
的值而变化
7.已知线段AD∥平面α,且与平面α的距离等于4,点B是平面α内动点,且满足AB=5,若AD=10,则点D与点B的距离d满足 ( )
A. d的最大值为![]() ,无最小值
,无最小值
B. d的最小值为![]() ,无最大值
,无最大值
C.
d的最大值为![]() ,最小值
,最小值![]()
D. d的最大值为![]() ,最小值为
,最小值为![]()
8.三人传球由甲开始发球,并作第一传球,经5次传球后,球仍回到甲手中,则不同的传球方法共有 ( )
A. 6种 B. 8种 C. 10种 D. 16种
9.半径不等的两定圆![]() 无公共点,动圆
无公共点,动圆![]() 与
与![]() 都内切,则圆心O是轨迹是( )
都内切,则圆心O是轨迹是( )
A. 双曲线的一支 B. 椭圆
C. 双曲线的一支或椭圆 D. 抛物线或椭圆
10.正三棱锥![]() 的侧棱长和底面边长相等,如果E、F分别为SC,AB的中点,那么异面直线EF与SA所成角为 ( )
的侧棱长和底面边长相等,如果E、F分别为SC,AB的中点,那么异面直线EF与SA所成角为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.设二次函数![]() 对于任意t都有
对于任意t都有![]() ,且在闭区间[m,0]上有最大值5,最小值1,则m的取值范围是 ( )
,且在闭区间[m,0]上有最大值5,最小值1,则m的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12. 某地每年消耗木材约20万![]() ,每
,每![]() 价480元,为了减少木材消耗,决定按
价480元,为了减少木材消耗,决定按![]() 征收木材税,这样每年的木材消耗量减少
征收木材税,这样每年的木材消耗量减少![]() 万
万![]() ,为了既减少木材消耗又保证税金收入每年不少于180万元,则
,为了既减少木材消耗又保证税金收入每年不少于180万元,则![]() 的范围是 ( )
的范围是 ( )
A. [1,3] B.[2,4]
C. [3,5] D.[4,6]
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.答案填在题中横线上.
13.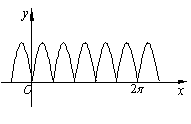 右图表示周期函数y=f(x)的变化规律,由
图象可以观察 出f(x)的最小正周期是_______.
右图表示周期函数y=f(x)的变化规律,由
图象可以观察 出f(x)的最小正周期是_______.
14.要制造一个底面半径为4cm,母线长为6cm的圆锥,用一块长方形材料做它的侧面,这样的长方形的长与宽的最小值分别是 .
15.在二项式![]() 和
和![]() 的展开式中,各项系数之和记为
的展开式中,各项系数之和记为![]() 是正整数,则
是正整数,则![]() =
=![]()
16.函数f(x)满足f(nx)=[ f(x)]n,写出一个满足上述条件的函数_______.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
是否存在常数c,使得不等式![]() 对任意正实数x、y恒成立?证明你的结论.
对任意正实数x、y恒成立?证明你的结论.
注意:考生在(18甲)、(18乙)两题中选一题作答,如果两题都答,只以(18甲)计分.
18.(本小题满分12分)
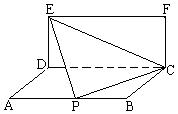
(甲)如图,已知矩形ABCD和矩形CDEF所在平面互相垂直,
(I)如果AB=2,P为AB中点,求点P到平面CDEF的距离及二面角D—EC—P的正切值;
(II)设AB=a,问在线段AB上是否存在点P使得EP⊥PC,并说明理由.
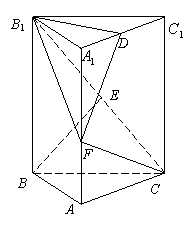 (乙) 如图,直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=
(乙) 如图,直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=![]() ,BB1=
,BB1=![]() ,D为A1C1的中点,E为B1C的中点,
,D为A1C1的中点,E为B1C的中点,
(Ⅰ)求直线BE与A1C所成的角;
(Ⅱ)在线段AA1上是否存在点F,使CF⊥平面B1DF,若存在,求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
19.(本小题满分12分)
若数列![]() 满足对一切
满足对一切![]() ,
,![]() ,且
,且![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项的和,求证:
项的和,求证:
(I)![]()
(II)![]()
20.(本小题满分12分)
已知:有6个房间安排4个旅游者住,每人可以进住任一房间,且进住房间是等可能的,试求下列各事件的概率:
(I)事件A:指定的4个房间各有1人;
(II)事件B:恰有4个房间各有1人;
(III)事件C:指定的某个房间有2人.
21.(本小题满分14分)
在平行四边形ABCD中,A(1,1),![]() ,点M是线段AB的中点,线段CM与BD交于点P.
,点M是线段AB的中点,线段CM与BD交于点P.
(I)若![]() ,求点C的坐标;
,求点C的坐标;
(II)当![]() 时,求点P的轨迹.
时,求点P的轨迹.
22.(本小题满分14分)
已知函数f(x)=x3+(b-1)x2+cx(b、c为常数).
(I) 若f(x)在x=1和x=3处取的极值,试求b、c的值;
(II) 若f(x)在x∈(-∞,x1)、(x2,+∞)上单调递增且在x∈(x1,x2)上单调递减,又满足
x2-x1>1,求证:b2>2(b+2c);
(III)在(2)的条件下,若t<x1,试比较t2+bt+c与x1的大小,并加以证明.
高中学生学科素质训练
高三数学同步测试(4)参考解答
一、选择题
1.C 2.C 3.D 4.A 5.C 6.C 7.D 8.C 9.C 10.C 11.B 12.C
二、填空题
13.![]() 14.12cm, 9cm. 15.
14.12cm, 9cm. 15. ![]() 16.f(x)=
16.f(x)=![]() 等.
等.
三、解答题
17.当![]() 时,由已知不等式得
时,由已知不等式得![]() …3分 下面分两部分给出证明:
…3分 下面分两部分给出证明:
⑴先证![]() ,
,
此不等式![]()
![]()
![]() ,此式显然成立; ………………7分
,此式显然成立; ………………7分
⑵再证![]() ,
,
此不等式![]()
![]()
![]() ,此式显然成立.………10分
,此式显然成立.………10分
综上可知,存在常数![]() ,是对任意的整数x、y,题中的不等式成立.……12分
,是对任意的整数x、y,题中的不等式成立.……12分
18. (甲小题)
(I) 过P作PQ⊥CD于Q,则PQ=AD=1. ∵平面ABCD⊥平面CDEF, ∴PQ⊥平面CDEF.
∴点P到平面CDEF的距离为1. ………2分
过P作PR⊥EC于R,连结QR,则QR⊥EC.
∴∠PRQ为二面角D—EC—P的平面角. ………4分∵![]() , △PQR中,PQ⊥QR.
, △PQR中,PQ⊥QR.
∴tan∠PRQ=![]() ………… 6分
………… 6分
(II)假定线段AB上存在点P使得EP⊥PC
连结PD,由ED⊥平面ABCD知
EP⊥PC![]() PD⊥PC …………8分 设∠BCP=
PD⊥PC …………8分 设∠BCP=![]() ,则BP=tan
,则BP=tan![]() ,AP=cot
,AP=cot![]() .
.
∵AB=AP+PB,
∴tan![]() +cot
+cot![]() =a, a………10分 ∵tan
=a, a………10分 ∵tan![]() +cot
+cot![]() ≥2,
≥2,
∴当a≥2时, 存在点P, 使EP⊥PC;
当0<a<2时, 不存在点P, 使EP⊥PC. ………12分
18(乙小题)
(Ⅰ)以![]() 为原点,建立如图所示的空间直角坐标系. ……2分
为原点,建立如图所示的空间直角坐标系. ……2分
![]()
![]()
![]() ,…………3分
,…………3分
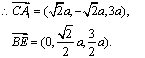 ,
,![]() ,
,
![]() ,
,
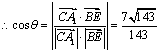 . ……………5分
. ……………5分
故![]() 与
与![]() 所成的角为
所成的角为![]() .
…………6分
.
…………6分
(Ⅱ)假设存在点![]() ,使
,使![]() ,不妨设
,不妨设![]() ,
,
![]() ,
,
![]() ,……………8分
,……………8分
![]() ……………………9分
……………………9分
由![]() , ……………11分
, ……………11分
故当![]() .……………………12分
.……………………12分
19.(I) 由![]() ,得
,得
![]() ……………4分
……………4分
所以
![]() …………6分
…………6分
(II)
由![]() ,得
,得
![]() ,
,
![]() ,
,
![]() ……,
……,
![]() ,
……………8分
,
……………8分
叠加这![]() 个不等式,得
个不等式,得
![]() , ……………10分
, ……………10分
即 ![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() …………12分
…………12分
20.由于每人可进住任1房间,进住哪间房是等可能的,每人都有6种等可能的方法, 根据乘法原理,4人进住6个房间共有64种方法
(I)指定的4个房间各有1人,有![]() 种方法,
种方法,![]() . …………4分
. …………4分
(II)从6间中选出4间有![]() 种方法,4个人每人去1间有
种方法,4个人每人去1间有![]() 种方法,
种方法,
![]()
![]() . ………8分
. ………8分
(III)从4人中选2个人去指定的某个房间,共有![]() 种选法,余下2人每人都可去5个房间中的任1间,因而有52种种方法.
种选法,余下2人每人都可去5个房间中的任1间,因而有52种种方法.![]() . ……………12分
. ……………12分
21. (I)设点C坐标为(![]() .
.
又![]() ,
……………3分
,
……………3分
即 ![]() ,
,
![]() , 即点C(0,6).
…………6分
, 即点C(0,6).
…………6分
(II)设![]() ,则
,则 ![]() ,…………8分
,…………8分
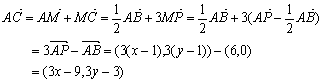
……………10分
![]()
![]() ABCD为菱形.
ABCD为菱形.
![]()
![]()
![]() .
…12分
.
…12分
故点P的轨迹是以(5,1)为圆心,2为半圆去掉与直线![]() 的两个交点. …………14分
的两个交点. …………14分
22. (I) f/(x)=x2+(b-1)x+c , ……………2分
据题意知,1和3是方程x2+(b-1)x+c=0的两根,
∴1-b=1+3=4, c=1×3=3,即b=-3, c=3 ……………4分
(II) 由题意知,当x∈(-∞,x1)、(x2,+∞)时, f/(x)>0;
当x∈(x1,x2)时, f/(x)<0. ……………6分
所以x1、x2是方程x2+(b-1)x+c=0的两根,则x1+x2=1-b, x1x2=c.
∴b2-2(b+2c)= b2-2b-4c=[1-(x1+x2)2]-2[1-(x1+x2)]-4x1x2=(x1+x2)2-1
∵x2-x1>1, ∴(x1+x2)2-1>0 ∴b2>2(b+2c). ……………9分
(III)在(II)的条件下,由上题知x2+(b-1)x+c=(x-x1)(x-x2)
即x2+bx+c=(x-x1)(x-x2)+ x ……………11分
所以 (t2+bt+c)-x1=(t-x1)(t-x2)+t-x1=(t-x1)(t+1-x2)
∵x2>1+x1>1+t,
∴1+t-x2<0.
又0<t<x1 ∴t-x1<0.
∴(t-x1)(t+1-x2)<0,
故t2+bt+c>x1. ……………14分