下学期
高中学生学科素质训练
高三数学同步测试(5)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P. ![]()
那么n次独立重复试验中恰好发生k次的概
率 其中R表示球的半径
![]()
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.下列不等式的在区间![]() 内恒成立的是 ( )
内恒成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.圆锥的侧面展开图是一个半径为12的半圆,则这个圆锥的内切球的体积是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知z∈C,满足不等式![]() 的点Z的集合用阴影表示为 ( )
的点Z的集合用阴影表示为 ( )
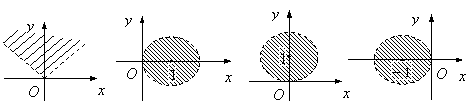 |
A. B. C. D.
4.一个单细胞以一分为二的方式,每3分钟分裂一次,恰一个小时充满某容器. 若开始时就放入两个单细胞,则充满容器的时间是 ( )
A. 正好半小时 B. 大于45分钟,小于50分钟
C. 大于50分钟,小于55分钟 D. 大于55分钟, 小于60分钟
5. 下列函数关系中,可以看作二次函数y=ax2+bx+c模型的是 ( )
A. 汽车的行驶公里数与耗油量的关系
B.我国人口年自然增长率为1%,这样我国人口总数随年份的变化关系
C.竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力)
D.核电站中,作为核燃料的某放射元素裂变后所剩的原子数随使用时间的变化关系
6. 如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是
( )
如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是
( )
A.6![]() 米 B.6
米 B.6![]() 米
米
C.3![]() 米 D.3
米 D.3![]() 米
米
7.设a<c<b,如果把函数![]() 的图象被两条平行的直线
的图象被两条平行的直线![]() 所截的一段近似地看作一条线段,则下列关系式中,
所截的一段近似地看作一条线段,则下列关系式中,![]() 的最佳近似表示式是 ( )
的最佳近似表示式是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.过球面上三点A、B、C的截面和球心的距离是球半径的一半,且AB=6,BC=8,AC=10,
则球的表面积是 ( )
A.100![]() B.300
B.300![]() C.
C.![]()
![]() D.
D.![]()
![]()
9.已知点P在定圆O的圆内或圆周上,圆C经过点P且与定圆O相切,则动圆C的圆心轨迹是 ( )
A.圆或椭圆或双曲线 B.两条射线或圆或抛物线
C.两条射线或圆或椭圆 D.椭圆或双曲线和抛物线
10.甲、乙两名篮球队员轮流投篮直至某人投中为止,每次投篮甲投中的概率为0.4,乙投中的概率为0.6,且不受其它投篮结果的影响.设甲投篮的次数为![]() ,若甲先投,则
,若甲先投,则![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.二次曲线![]() ,当
,当![]() 时,该曲线的离心率
时,该曲线的离心率![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.磁悬浮列车是一种高科技含量的新型交通工具,它具有速度快,爬坡能力强,能耗低等优点,其每个座位的平均能耗仅是飞机每个座位平均能耗的三分之一,是汽车每个座位平均能耗的70%,那么汽车每个座位的平均能耗是飞机每个座位平均能耗的 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.答案填在题中横线上.
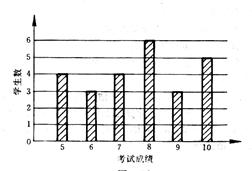 13.一个班级的考试成绩如图所示,求其
13.一个班级的考试成绩如图所示,求其
平均成绩(取靠近平均成绩的整数)________.
14.某医药研究所研制了5种消炎药X1、X2、X3、X4、X5和4种退烧药T1、T2、T3、T4,现从中取出两种消炎药和一种退烧药同时使用进行疗效试验,但又知X1、X2两种消炎药必须同时搭配使用,但X3和T4两种药不能同时使用,则不同的试验方案有 种(用数字作答).
15.在二项式定理![]()
![]() 的两边求导后,再取
的两边求导后,再取![]() ,得恒等式_______________________________________.
,得恒等式_______________________________________.
16.已知集合![]() ,对它的非空子集A,可将A 中每个元素k,都乘以
,对它的非空子集A,可将A 中每个元素k,都乘以![]() 再求和(如A={1,3,6},可求得和为
再求和(如A={1,3,6},可求得和为![]() ,则对M的所有非空子集,这些和的总和是
.
,则对M的所有非空子集,这些和的总和是
.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知a=(cosα,sinα), b=(cosβ,sinβ),其中0<α<β<π.
(I)求证:a+b 与a-b互相垂直;
(II)若ka+b与a-kb的长度相等,求β-α的值(k为非零的常数).
注意:考生在(18甲)、(18乙)两题中选一题作答,如果两题都答,只以(18甲)计分.
18.(本小题满分12分)
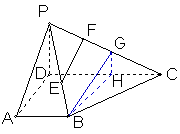
(甲) 如图,已知四棱锥P—ABCD的侧面PAD与底面ABCD垂直,△PAD是边长为a的正三角形,ABCD为直角梯形, AB//CD,DC=2a,∠ADC=90°,∠DCB=45°,E为BP中点,F在PC上且PF=
如图,已知四棱锥P—ABCD的侧面PAD与底面ABCD垂直,△PAD是边长为a的正三角形,ABCD为直角梯形, AB//CD,DC=2a,∠ADC=90°,∠DCB=45°,E为BP中点,F在PC上且PF=![]() PC.
PC.
(Ⅰ)求证EF//平面PAD;
(Ⅱ)求三棱锥E—PCD的体积.
(乙) 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a(a>0),BB1=3a,D为A1C1的中点,E为B1C的中点.
(I)求直线BE与A1C所成的角θ;
(II)在线段AA1上取一点F,问AF为何值时,CF⊥平面B1DF?
19.(本小题满分12分)
某银行准备新设一种定期存款业务,经预测存款量与利率的平方成正比,比例系数为k(k>0),贷款的利率为4.8%。又银行吸收的存款能全部放贷出去。
(I)若存款的利率为x,x∈(0,0.048),试写出存款量g(x)及银行支付给储户的利息h(x);
 (II)存款利率定为多少时,银行可获得最大利益?
(II)存款利率定为多少时,银行可获得最大利益?
20.(本小题满分12分)
在一很大的湖岸边(可视湖岸为直线)停放着一只小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成15°角,速度为2.5km/h,同时岸边有一人,从同一地点开始追赶小船,已知他在岸上跑的速度为4km/h,在水中游的速度为2km/h.,问此人能否追上小船.若小船速度改变,则小船能被人追上的最大速度是多少?
21.(本小题满分14分)
设![]() ,常数
,常数![]() ,定义运算“
,定义运算“![]() :
:![]() ”;“ :
”;“ :![]()
![]() ”
”
![]() (I)若
(I)若![]() ,求动点
,求动点![]() [(
[(![]() )
)![]()
![]() ]1/2)的轨迹C的方程;
]1/2)的轨迹C的方程;
(II)已知直线![]() 与(1)中的轨迹C交于
与(1)中的轨迹C交于![]() 两点,
两点,
![]()
![]() 若[(
若[(![]()
![]() )+(
)+(![]()
![]() )]1/2=
)]1/2=![]() ,试求
,试求![]() 的值;
的值;
![]() (III)设
(III)设![]() 是平面上任意一点,定义
是平面上任意一点,定义![]() {
{![]()
![]()
![]() }1/2,
}1/2,
![]()
![]() [
[![]()
![]() ]1/2,在轨迹C上是否存在两点
]1/2,在轨迹C上是否存在两点![]() ,使其满足
,使其满足![]() ,
,
若存在,请求出![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
22.(本小题满分14分)
对于函数![]() ,若存在
,若存在![]() 成立,则称
成立,则称![]() 的不动点。如果函数
的不动点。如果函数![]() 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且![]()
(I)求函数![]() 的解析式;
的解析式;
(II)已知各项不为零的数列![]() ,求数列通项
,求数列通项![]() ;
;
(III)如果数列![]() 满足
满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立.
成立.
高中学生学科素质训练
高三数学同步测试(5)参考答案
一、选择题
1.C 2.D 3.C 4.D 5.C 6.A. 7.A 8.D 9.C 10.B 11.C 12.C
二、填空题
13. 8 14. 14 15. ![]() 16. 2560
16. 2560
三、解答题
17.(I)由题意a+b=(cosα+cosβ, sinα+sinβ), a-b=(cosα-cosβ, sinα-sinβ)
∵(a+b)·(a-b)= (cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)
= cos2α-cos2β+ sin2α-sin2β=1-1=0
∴a+b 与a-b互相垂直.
(II) ka+b=(kcosα+cosβ,ksinα+sinβ), a-kb=(cosα-kcosβ, sinα-ksinβ)
ka+b![]() =
=![]() ,
a-kb=
,
a-kb=![]()
由题意,得4cos(β-α)=0, 因为0<α<β<π ,所以β-α=![]()
18. (甲小题)(I)∵侧面PAD⊥底面ABCD, CD⊥AD,
 ∴CD⊥平面PAD. …………………2分
∴CD⊥平面PAD. …………………2分
同理AB⊥平面PAD且AB⊥AP
取DC、PC中点为H、G,连结BH、HG, 则BH⊥DC
又∠BCH=45°∴∠CBH=45°
由AB=AP=a,CH=HB=a,![]()
又CD=2a, DP=a, ![]() …………………4分
…………………4分
△PBC中,G为PC中点,∴BG⊥PC
易得![]() .
…………………6分
.
…………………6分
∴△BGH为直角三角形,且BG⊥GH, ∴GB⊥平面PDC.
∴GB⊥CD. 又CD⊥HB, ∴CD⊥平面BGH, ∴平面BGH∥平面PAD.
∴BG∥平面PAD ∵EF∥BG , ∴EF∥平面PAD. …………………8分
(II)∵BG⊥平面PDC,EF∥BG , ∴EF⊥平面PDC.
∴EF为三棱锥E—PDC的高, …………………10分
且EF=![]() ,
,
![]() ,
,
故 ![]() .
…………………12分
.
…………………12分
18. (乙小题)
 (I) 以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系.
(I) 以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系.
∵AC=2a,∠ABC=90º.
∴AB=BC=a.
从而B(0,0,0),A(a,0,0),C(0,a,0),
A1(a,0,3a),B1(0,0,3a),C1(0,a,3a),
D(,3a),E(0,).………………2分
∴).
而 . ………4分
∴cosθ=
∴θ=arctan …………6分
(II)设AF=x,则F( a,0,x) …………7分
+x×0=0 ∴……………10分
要使得CF⊥平面B1DF,只需CF⊥B1F 由=2a2+x(x-3a)=0 有x=a或x=2a
故当AF=a,或AF=2a时,CF⊥平面B1DF.
…………………12分
19. (I)由题意,存款量g(x)=kx2,银行应支付的利息h(x)=x·g(x)=kx3 . ……4分
(II)设银行可获收益为y, 则y=0.048·kx2- kx3 ;
y/=0.096·kx-3kx2 …………………6分
令y/=0即0.096·kx-3kx2=0 解得x=0或x=0.032
又当x∈(0,0.032)时 , y/>0,当 x∈(0.032,0.048)时,y/<0. ………8分
∴y在(0,0.032)内单调递增,在(0.032,0.048)内单调递减;
故当x=0.032时, y在(0,0.048)内取得极大值,也是最大值.
故存款的利率为3.2%,银行可获得最大收益. ………………12分
20.设船速为v,显然![]() 时人是不可能追上小船,当
时人是不可能追上小船,当![]() km/h时,人不必在岸上跑,而只要立即从同一地点直接下水就可以追上小船,因此只要考虑
km/h时,人不必在岸上跑,而只要立即从同一地点直接下水就可以追上小船,因此只要考虑![]() 的情况,由于人在水中游的速度小于船的速度,人只有先沿湖岸跑一段路后再游水追赶,当人沿岸跑的轨迹和人游水的轨迹以及船在水中漂流的轨迹组成一个封闭的三角形时,人才能追上小船.设船速为v,人追上船所用时间为t,人在岸上跑的时间为
的情况,由于人在水中游的速度小于船的速度,人只有先沿湖岸跑一段路后再游水追赶,当人沿岸跑的轨迹和人游水的轨迹以及船在水中漂流的轨迹组成一个封闭的三角形时,人才能追上小船.设船速为v,人追上船所用时间为t,人在岸上跑的时间为![]() ,则人在水中游的时间为
,则人在水中游的时间为![]() ,人要追上小船,则人船运动的路线满足如图所示的三角形.……………4分
,人要追上小船,则人船运动的路线满足如图所示的三角形.……………4分
![]() 由余弦是理得
由余弦是理得
![]() ………………6分
………………6分
即![]()
整理得![]() .
………………8分
.
………………8分
要使上式在(0,1)范围内有实数解,则有![]() 且
且![]()
解得![]() .
………………10分
.
………………10分
故当船速在![]() 内时,人船运动路线可物成三角形,即人能追上小船,船能使人追上的最大速度为
内时,人船运动路线可物成三角形,即人能追上小船,船能使人追上的最大速度为![]() ,由此可见当船速为2.5km/h时, 人可以追上小船.
,由此可见当船速为2.5km/h时, 人可以追上小船.
………………12分
21. (I)先读懂定义的符号,再从动点轨迹入手,设![]() ,则
,则![]() ,所以
,所以![]() .
.
故所求轨迹C的方程为![]() .
………………4分
.
………………4分
(II)注意挖掘隐含条件,由![]() 得
得![]() ,由
,由![]() 得
得![]() , 6分
, 6分
由根与系数关系得:![]() ,由
,由
![]()
![]() [(
[(![]()
![]() )+(
)+(![]()
![]() )]1/2=
)]1/2=![]() 得
得![]() ,
,
即![]() ,所以
,所以![]() (舍去) .
(舍去) .
………………8分
(III)设C上存在两点![]() 满足:
满足:![]() ,
,
则有
![]() ,
,
即
![]() , ………10分
, ………10分
所以![]() 是方程
是方程
![]() 的两根,且
的两根,且![]() ,
,
所以
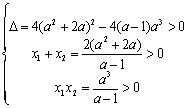 解得
解得 ![]() ,…………12分
,…………12分
所以,当![]() 时,存在满足条件的两点;当
时,存在满足条件的两点;当![]() 时,不存在满足条件的两点.
时,不存在满足条件的两点.
………………14分
22.(I) 依题意有![]() ,化简为
,化简为 ![]() 由违达定理, 得
由违达定理, 得 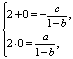
解得 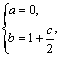 ……………2分
……………2分
代入表达式![]() ,由
,由![]()
得 ![]() 不止有两个不动点,
不止有两个不动点,
![]() ………………4分
………………4分
(II)由题设得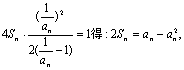 (*)
(*)
且![]() (**)
(**)
………………6分
由(*)与(**)两式相减得:
![]()
![]()
解得![]() (舍去)或
(舍去)或![]() ,由
,由![]() ,若
,若![]() 这与
这与![]() 矛盾,
矛盾,![]() ,即{
,即{![]() 是以-1为首项,-1为公差的等差数列,
是以-1为首项,-1为公差的等差数列,![]() . ………9分
. ………9分
(III)采用反证法,假设![]() 则由(I)知
则由(I)知![]()
![]() ,
,
有![]() ,而当
,而当![]()
这与假设矛盾,故假设不成立.
![]() ……………14分
……………14分