高三数学统一考试（理工类）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。考试时间为120分种。
第Ⅰ卷（选择题，共60分）
一、 选择题：本大题共12小题，每小题5分；共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1、 已知集合M=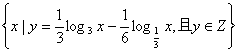
,若
,则
的值可以是（ ）
A
B 
C 3
D 9
2、下列命题正确的是（ ）
A 若A(-2,4), B(2,1)则
与x轴正方向的夹角为
B
C 
D 若
为非零向量，且
则
3、已知钝角
的终边经过点
，且
，则为（ ）
A 
B 
C 
D 
4、已知、b为不相等的两个正数，若A是、b的等差中项，正数G是、b的等比中项，则（ ）
A 
B 
C 
D
5、已知椭圆的左、右焦点分别是
，以
为圆心作圆经过椭圆中心，且与椭圆相交于M点，直线
与圆相切，则该椭圆的离心率e=(
)
A 
B 
C
D 
6、已知正四棱锥以棱长为1的正方体的某个面为底面，且与该正方体有相同的全面积，则这一正四棱锥的侧棱与底面所成的角的余弦值为（ ）
A 
B 
C 
D 
7、不等式组
，表示的平面区域的面积是（ ）
|
8、使
的展开式中存在常数项的最小正整数n=（ ）
A 10 B 8 C 5 D 3
9、已知
对于任意实数x有
成立，且
，则实数
的值为（ ）
A
B 
C —1或３
D －３或１
10、在棱长为1的正方体
中，对角线
上有一条动线段PQ，若已知ＰＱ为定值，则能成为定值的是（
）
A 点Q到直线PB的距离 B 点P到平面BQD的距离
C 直线PQ与直线DB的距离 D 直线PQ与平面PBD所成的角
11、设p: 函数
是偶函数, q:
是奇函数,则p是q的（ ）
A 充分不必要条件 B 必要不充分条件
C 充要条件 D 既不充分也不必要条件
12、虚数
满足：
，则这样不同的虚数共有（ ）个
Ａ ３０ Ｂ ２７ Ｃ ２４ Ｄ２１
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分；共16分. 把答案填在题中横线上.
１３、有一个正多面体，其面数＋顶点数＝８，且各条棱长都等于４，则这一多面体的外接球的体积是
14、一个田径队，有男运动员56人，女运动员12人，比赛后，立即用分层抽样的方法，从全体队员中抽出一个容量为28的样本进行尿样兴奋剂检查，其中男运动员应抽 人
15、若数列
满足
且
则
16已知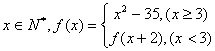
其中值域设为D，给出下列数值：-26，-1，9，11，27，65，则其中属于集合D的元素是
（写出所有可能的数值）。
13 14 15 16
三、解答题：本大题6小题. 共74分.解答应写出文字说明、证明过程或推演步骤.
17、（本小题满分12分）
函数
，且
。
（1） 求
的最大值和最小值；
（2） 若
，求
的值。
|
18、（本小题满分12分）
已知条件
和条件
，请选取适当的实数的值，分别利用所给的两个条件作为A、B构造命题：“若A则B”，并使得构造的原命题为真命题，而其逆命题为假命题。则这样的一个原命题可以是什么？并说明为什么这一命题是符合要求的命题。
19、(本小题满分12分)
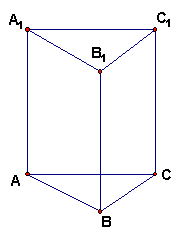如图所示,已知正三棱柱
的底面边长为1，若点M在侧棱
上,且AM与侧面
所成的角为;
(Ⅰ)若BM=
,求
与
所成的角；
(Ⅱ)判断棱柱的高等于多少时能使得
? 请给出证明.
|
20、(本小题满分12分)
某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命,可以进行第二次射击,但目标已在150m处,这时命中记2分,且停止射击；若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击；若三次都未命中,则记0分。已知射手甲在100m处击中目标的概率为
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
(Ⅰ) 求这名射手在三次射击中命中目标的概率;
(Ⅱ) 求这位射手在这次射击比赛中得分的数学期望.
21、(本小题满分12分)
设函数与数列满足关系：
①
,其中是方程
的实数根；
②
；
③的导数
。
(Ⅰ) 证明：
；
(Ⅱ) 判断
与
的大小,并证明你的结论。
|
22.(本小题满分14分)
已知A、B是椭圆
的一条弦,向量
与AB交于M,且
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线AB交于N(4,-1).
（1）求椭圆的离心率
；
（2）设双曲线的离心率为
求
的解析式,并求它的定义域和值域.
参考答案（详细答案见《中国考试》第3、4期）
一、 选择题
DCDAC ABCDC CB
二、填空题
13、8
14、16 15、
16、-26、14、65
三解答题
17、（1）
（2）
18、
19、（1）与所成的角为
(Ⅱ)棱柱的高等于时能使得
20、(Ⅰ) 这名射手在三次射击中命中目标的概率95/144
(Ⅱ) 这位射手在这次射击比赛中得分的数学期望85/48.
21、（1）用数学归纳法
（2）求导研究单调性
22、（1）椭圆的离心率
；
（2）
，它的定义域
值域.