高三数学新编立体几何内容分析及复习建议
一、 教材、考试要求的变化
新教材立体几何内容变化较大,主要是删去了棱台、旋转体、球冠、多面体及旋转体体积等;增加了正多面体的概念,多面体的欧拉公式,最大变化是首次引入空间向量,并用这一工具去解决空间直线的平行、垂直关系,以及求空间的“距离”、“角”。从近几年的高考题来看,新教材的甲组题(即9B考题)比乙组题(即9A考题)和全国题都容易做。还有用向量方法去解部分传统的立体几何题也是有优势的,如2000、2003年全国高考立体几何题,普遍都认为较难,但如果用向量方法去解,就很简单了。因此,要重点掌握“空间向量”,并突出其“工具性”。
二、立几题的空间向量解法分析
利用空间向量解立几题,体现了空间的数形结合思想,顺应了几何改革代数化的方向;利用空间向量解立几题,首先应是确定基向量。即![]() 或单位正交基底
或单位正交基底![]() 。
。
1、利用空间向量解线线平行、垂直问题
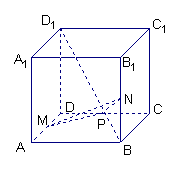 【例1】(2003全国节选)正方体
【例1】(2003全国节选)正方体![]() 中,
中,![]() 分别为
分别为![]() 的中点,证明:
的中点,证明:![]() 与平面
与平面![]() 不垂直。
不垂直。
分析:用传统方法证明![]() 与
与![]() 不垂直,有难度;
不垂直,有难度;
利用向量:![]() ,
,
![]() ,所以
,所以![]() 与
与![]() 不垂直。
不垂直。
【例2】(2003全国)如图,直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,
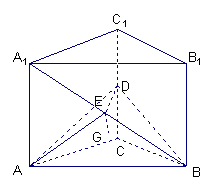
![]() ,侧棱
,侧棱![]() 分别是CC1与A1B的
分别是CC1与A1B的
中点,点E在平面ABD上的射影是△ABD的重心G。
(1)求A1B与平面ABD所成角的大小(结果用反三
角函数值表示);
(2)求点A1到平面AED的距离.
简析:传统解法解此题难点一是重心G的运用,而用向
量解:由![]() 很快得
很快得![]() ,
,
二是如何由条件求出![]() 的长,应用向量则由
的长,应用向量则由![]() 与
与![]() 垂直易得
垂直易得![]() 。
。
2、利用空间向量解探索性问题
对于立几中的探索性问题及存在性问题,用“形”解难度很大,而“数”中的待定系数法正好运用。
 【例3】(2000全国节选)如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°。
【例3】(2000全国节选)如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°。![]() 的值
的值
为多大时,能够使A1C⊥平面C1BD ? 请给出证明。
解:设![]() ,
,![]()
![]() ,则
,则![]() ,
,
当![]() 时
时![]()
![]() ,解得
,解得![]() ,所以
,所以![]() =1时A1C⊥平面C1BD。
=1时A1C⊥平面C1BD。
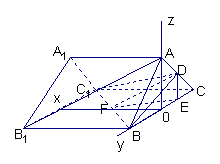 【例4】(94全国节选)如图,已知
【例4】(94全国节选)如图,已知![]() 是正三棱柱,
是正三棱柱,![]() 是
是![]() 的中点,
的中点,![]() ,求二面角
,求二面角![]() 的度数。
的度数。
简析:此题学生很易作出二面角的平面角![]() ,
,
但用传统方法难以求出![]() 与
与![]() 的长度关系;
的长度关系;
若用向量解:在如图坐标系下,设![]() ,
,
![]() 则
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() 得,
得,![]() ,
,![]() ,很快得出结论。
,很快得出结论。
3、利用平面的法向量求解角和距离问题
当作平面的垂线难度较大时,可利用平面的法向量求解一些角和距离问题。如图,平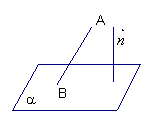 面
面![]() 的法向量为
的法向量为![]() ,
,![]() 为平面
为平面![]() 的斜线,
的斜线,![]() 为斜足,则
为斜足,则
![]() 与平面
与平面![]() 所成的角
所成的角![]() ;用向量在法向量
;用向量在法向量
上的投影公式易得:点![]() 到平面
到平面![]() 的距离
的距离
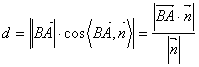 ;当
;当![]() 与异面直线
与异面直线![]() ,
,![]() 都垂直时,
都垂直时,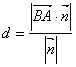 为异面直线
为异面直线![]() ,
,![]() 的距离公式。设二面角
的距离公式。设二面角![]() ,
,![]() 分别为平面
分别为平面![]() 的法向量,则二面角
的法向量,则二面角![]() 的大小为
的大小为![]() 或它的补角。
或它的补角。
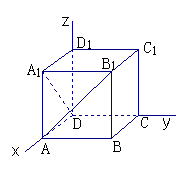 【例5】(教材习题)棱长为1的正方体
【例5】(教材习题)棱长为1的正方体![]() 中,
中,
求面对角线![]() 和
和![]() 的距离。
的距离。
解:建立如图直角坐标系,则![]()
![]() ,设
,设![]() ,由
,由![]() ,
,![]()
得![]() 令
令![]() ,则
,则![]() ,又
,又
![]() ,所以
,所以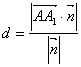
![]() 。
。
三、复习建议和能力要求
第二轮复习侧重的应是解题能力的培养,尤其是读题能力、类比能力和转化能力;对于立体几何的能力培养,我认为应从以下几方面着手:
1、重视已知条件与图形的对号入座
 解立几题一般需作好两个图,一是立体图,把已知条件中的线段长、角度值在图中标出,对于图形翻折、旋转等问题把折前及折后的长度、角度对应起来,往往发现解题思路或部分结论。二是用来计算的铅垂放置的平面图(解题关键图),利于正确运算。
解立几题一般需作好两个图,一是立体图,把已知条件中的线段长、角度值在图中标出,对于图形翻折、旋转等问题把折前及折后的长度、角度对应起来,往往发现解题思路或部分结论。二是用来计算的铅垂放置的平面图(解题关键图),利于正确运算。
【例6】(2003汕头一模)已知![]() 是矩形,
是矩形,![]() 平面
平面
![]() ,
,![]() ,
,![]() 分别是
分别是![]()
的中点;(1)求证:二面角![]() 是直二面角;
是直二面角;
(2)求点![]() 到平面
到平面![]() 的距离。
的距离。
简析:依次标出已知条件得到![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,从而(1)得到证明,(2)也可利用
,从而(1)得到证明,(2)也可利用![]() 到平面
到平面![]() 的距离为
的距离为![]() 到平面
到平面![]() 的距离的一半得以很快解决。
的距离的一半得以很快解决。
2、重视常见体在解题中的利用
著名数学家波利亚指出:试着解决一个容易着手的简单问题,特殊的问题,类似的问题。立体几何中也是如此,一些具有特殊条件问题利用特殊体去解决能使解题简捷明快。如正四面体可在正方体中截得,三射线两两垂直、锐角在一个平面上的射影为直角时可在长方体里找到,空间四射线两两夹角相等可在正四面体找到等。
 【例7】(2003全国高考)一个四面体的所有棱长都为
【例7】(2003全国高考)一个四面体的所有棱长都为![]() ,四个顶点在同一球面上,则此球的表面积为A.3π B.4π C.
,四个顶点在同一球面上,则此球的表面积为A.3π B.4π C.![]() D.6π
D.6π
简析:棱长为1的正方体![]() 中,连接面对角线
中,连接面对角线![]()
![]() 得到四面体
得到四面体![]() 各棱长为
各棱长为![]() ,
,
从而得到球直径为![]() 。
。
【例8】(教科书复习参考题九![]() )
)![]() 是球面上四点,
是球面上四点,![]() 两两垂直,且
两两垂直,且
![]() ,求球的体积和面积。
,求球的体积和面积。
3、重视常规思路在解题中的应用
解立体几何题的一大难点是如何添加辅助线,而如何添加辅助线有一定规律。如:线段中点——用中位线;三角形等腰——底边上的中线垂直底边;两直线异面——平移为相交直线;具有面的垂线——用三垂线定理或逆定理;线面平行,面面垂直——用性质定理;同一点出发三直线两两垂直——建立空间直角坐标系等。这些常规通过讲练应使学生熟练掌握。
4、重视解题思维习惯的形成
养成良好的思维习惯,可避免小题大做,少走弯路。如求角度值时应:找角——作角——转移角——用向量计算![]() ;即先找现成的角,看看是否就是要求的角,不是的话试着作角,作角有难度的话通过平移转移角,实在不行用“数”解。类似的,求距离时应找高线——作高线——按比例转移——用向量计算等。
;即先找现成的角,看看是否就是要求的角,不是的话试着作角,作角有难度的话通过平移转移角,实在不行用“数”解。类似的,求距离时应找高线——作高线——按比例转移——用向量计算等。
总之,空间向量在立几中的应用,特别是用数量积求异面直线所成的角、斜线和平面所成的角、二面角的平面角;用向量在法向量上的投影求点到平面的距离,异面直线间的距离;用待定系数法求解立几开放题、探索题等。确实体现了它的强大功能。但不可否认,传统方法也有它的优越性,一旦空间的位置关系搞清楚了,计算量较小,正确率高。这“数”和“形”两条路应正确理解,合理选择。