高三数学第一学期期末统测试卷
高 三 数 学
命题人:周凯
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)部分。满分150分,时间120分钟。
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | ||
| 得分 | |||||||||
参考公式: 正棱锥、圆锥的侧面积公式
如果事件A、B互斥,那么
![]()
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中,c表示底面周长、l表示斜高或
P(A·B)=P(A)·P(B) 母线长
如果事件A在1次实验中发生的概率是 球的体积公式
P,那么n次独立重复实验中恰好发生k
![]()
次的概率 其中R表示球的半径
![]()
第I卷(选择题,共60分)
一. 选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内。
1.已知集合![]() 则必有 ------------------------------------( )
则必有 ------------------------------------( )
![]()
![]()
![]()
![]()
2.函数![]() 的图象经过点
的图象经过点![]() 则该函数的图象 -------------------------
( )
则该函数的图象 -------------------------
( )
A. 关于原点对称B. 关于![]() 轴对称C. 关于y轴对称 D. 关于直线
轴对称C. 关于y轴对称 D. 关于直线![]() 对称
对称
3.函数![]() 的反函数是 ----------------------------------- ( )
的反函数是 ----------------------------------- ( )
![]()
![]()
![]()
![]()
4.在![]() 的展开式中,
的展开式中,![]() 的系数为 --------------------------------------- ( )
的系数为 --------------------------------------- ( )
![]()
![]()
![]()
![]()
5.将函数![]() 的图象沿向量
的图象沿向量![]() 平移后所得图象的函数表达式为 ------------------------------------ ---- ( )
平移后所得图象的函数表达式为 ------------------------------------ ---- ( )
![]()
![]()
![]()
![]()
6.双曲线的焦距为4,两准线间的距离为3,则双曲线的离心率为 ------------( )
![]()
![]()
![]()
![]()
7.将5本不同的书全部分给4位同学,每人至少1本,则不同的分法种数为-----( )
A. 480 B. 240 C. 120 D. 96
8.![]() 的 ----------------------------------------------------------( )
的 ----------------------------------------------------------( )
A.充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
9.设![]() 为直线,
为直线,![]() 为平面,给出下列命题:
为平面,给出下列命题:
① ![]() ②
② ![]()
③ ![]() ④
④ ![]()
其中,正确的命题是------------------------------( )
A. ①② B. ①③ C. ②④ D. ③④
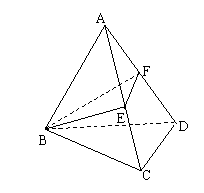
10.设四面体ABCD的各棱长均相等,E,F分别为AC,AD的中点(如图所示),则△BEF在该四面体的面ABC上的射影是-----------------------------------( )
 |
11.若曲线![]() 在点P处的切线平行于直线
在点P处的切线平行于直线![]() 则点P的坐标为-------( )
则点P的坐标为-------( )
A. (-1,3) B. (1,3) C. (-1,0) D. (1,0)
12.设A,B是两个独立事件,“A和B同时不发生”的概率为![]() “A发生且B不发生”的概率与“B发生且A不发生”的概率相等,则事件A发生的概率为------------------( )
“A发生且B不发生”的概率与“B发生且A不发生”的概率相等,则事件A发生的概率为------------------( )
![]()
![]() C.
C.
![]() D.
D.
![]()
第II卷(非选择题,共90分)
二. 填空题:本大题共4小题,每小题4分,共16分,把答案填在题中的横线上。
13.抛物线![]() 的焦点坐标是_______.
的焦点坐标是_______.
14.已知![]() _________.
_________.
15.已知![]() 满足条件
满足条件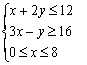 则
则![]() 的最大值为_________.
的最大值为_________.
16.已知某工厂生产某种产品的固定成本为2000万元,并且每生产一单位产品成本增加10万元,又知总收入R是单位产量Q的函数:![]() ,则总利润L(Q)的最大值为________万元.
,则总利润L(Q)的最大值为________万元.
三. 解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
已知![]() 的最小正周期为
的最小正周期为![]()
(1)
求函数![]() 的表达式;
的表达式;
(2)
若![]() 的值域。
的值域。
18.(本小题满分12分)
设![]() 为等差数列,
为等差数列,![]() 为等比数列,
为等比数列,![]() 分别求出
分别求出![]() 及
及![]() 的前10项的和
的前10项的和![]()
19(本小题满分12分)
已知函数![]() 在定义域(-1,1)上是减函数,且
在定义域(-1,1)上是减函数,且![]()
(1)
求![]() 的取值范围;
的取值范围;
(2)
试确定![]() 的取值范围,使得不等式
的取值范围,使得不等式![]() 成立。
成立。
20.(本小题满分12分)
四棱锥P-ABCD的底面是边长为![]() 的菱形,且
的菱形,且![]() 平面ABCD,E为PA的中点。
平面ABCD,E为PA的中点。
(1) 求证:平面EDB⊥平面ABCD;
(2)
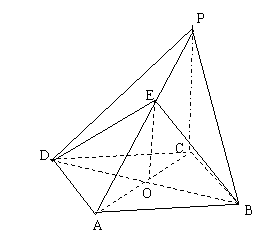 求点E到平面PBC的距离。
求点E到平面PBC的距离。
21.(本小题满分12分)
已知![]() 之间有关系式
之间有关系式![]() ,其中
,其中![]()
(1)
试用![]() ;
;
(2)
求![]() 的最大值,并求此时
的最大值,并求此时![]() 的夹角
的夹角![]() 的大小。
的大小。
22.(本小题满分14分)
已知椭圆![]() 的离心率
的离心率![]() 过点A(0,-b)和B(a,0)的直线与原点的距离为
过点A(0,-b)和B(a,0)的直线与原点的距离为![]()
(1) 求椭圆的方程;
(2)
设点P的坐标为(0,2),点Q的坐标为(-1,0),以(-1,k)(k≠0)为方向向量,且过点P的直线![]() 交椭圆于点C,D,试判断:是否存在k的值,使得点Q在以CD为直径的圆上?若存在,求出k的值;若不存在,请说明理由。
交椭圆于点C,D,试判断:是否存在k的值,使得点Q在以CD为直径的圆上?若存在,求出k的值;若不存在,请说明理由。
第一学期末统测试
高三数学参考答案及评分标准
一选择题:
1.B 2.C 3.A 4.C 5C 6.A 7.B 8.A 9.C 10.B 11D 12D
二填空题
13. ![]() 14.
14.
![]() 15.
10_ 16. 2500
15.
10_ 16. 2500
三解答题
17.(1)![]() ----------------3分
----------------3分
![]() ------------------------------------------ 5分
------------------------------------------ 5分
函数![]() 的表达式为:
的表达式为:![]() ---------------6分
---------------6分
(2)由![]() ---------------------------------8分
---------------------------------8分
![]() -------------------------------------------11分
-------------------------------------------11分
![]() ----------------------------------------------------12分
----------------------------------------------------12分
18.解:设等差数列![]() 的公差为
的公差为![]() 等比数列
等比数列![]() 的公比为
的公比为![]() -----------1分
-----------1分
![]() ①-------------------2分
①-------------------2分
又![]()
![]() ②--------3分
②--------3分
则由①,②得![]() ----------------------------------------------------------5分
----------------------------------------------------------5分
![]() --------------------------------------------------7分
--------------------------------------------------7分
将![]() 代入①,得
代入①,得![]() ---------------------------------9分
---------------------------------9分
当![]() 时,
时,![]() --------------------------------------------11分
--------------------------------------------11分
当![]() 时,
时,![]() -----------------------------------------12分
-----------------------------------------12分
19.解:(1)由![]() 在(-1,1)上是减函数,且
在(-1,1)上是减函数,且![]() 得
得![]() -------2分
-------2分
解得![]() ①------------------------------------------------------3分
①------------------------------------------------------3分
又由![]() 的定义域为(-1,1),得
的定义域为(-1,1),得![]() ------------------------------------------------------------------5分
------------------------------------------------------------------5分
解得![]() ②-------------------------------------------------6分
②-------------------------------------------------6分
故由①②得 ![]() ------------------------------------------------------7分
------------------------------------------------------7分
(2)![]() ------------------------------------------------------9分
------------------------------------------------------9分
此时,不等式可表示为![]() 即
即![]() -----------11分
-----------11分
解得 ![]() -------------------------------------------------------12分
-------------------------------------------------------12分
20.解:(1)连结EO-----------------------------------------------------------1分
∵ABCD为菱形,∴O为AC的中点----------------------2分
而E为PA的中点,∴EO//PC-------------------------------4分
又∵PC⊥平面ABCD,∴EO⊥平面ABCD--------------6分
而EO![]() 平面EDB,∴平面EDB⊥平面ABCD---------7分
平面EDB,∴平面EDB⊥平面ABCD---------7分
(2)∵EO//PC,且EO![]() 平面PBC,PC
平面PBC,PC![]() 平面PBC,
平面PBC,
∴EO//平面PBC------------------------------------------------9分
过点O作OF⊥BC,交BC于F,则OF的长就是点E
到平面PBC的距离---------------------------------------------10分
在Rt△COF中,![]()
![]() --12分
--12分
∴点E到平面PBC的距离为![]() ---------------------------------12分
---------------------------------12分
21.解:(1)由关系式![]() 得
得![]() --------1分
--------1分
![]() ---------------------------------------------------2分
---------------------------------------------------2分
![]()
![]() ---------------------3分
---------------------3分
又![]() --------------------------------------------4分
--------------------------------------------4分
![]() -----------------------------------6分
-----------------------------------6分
(2)![]() -----------------------------8分
-----------------------------8分
![]() ---------------------------------------------------------------9分
---------------------------------------------------------------9分
![]() 的最大值为
的最大值为![]() -------------------------------------------------------10分
-------------------------------------------------------10分
此时,![]() ---------------------------------------11分
---------------------------------------11分
又![]() 取得最大值时,
取得最大值时,![]() --------12分
--------12分
22.解:(1)设![]() 由题意,得
由题意,得![]() ----2分
----2分
由题意,得直线AB的方程![]() ------------------3分
------------------3分
又由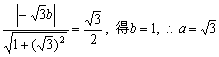 ----------------------------4分
----------------------------4分
∴所求椭圆方程为![]() --------------------------------------5分
--------------------------------------5分
(2)设点C,D的坐标分别为![]()
由题意,得直线![]() 的方程为
的方程为![]() ① --------------6分
① --------------6分
将①代入椭圆方程,消去y,得![]() -------7分
-------7分
![]() ② ----------------------8分
② ----------------------8分
要使点Q在以CD为直径的圆上,必须
![]()
![]() -----------------10分
-----------------10分
![]() ③
③
![]() ④ -------------------------11分
④ -------------------------11分
由②③④,解得![]() ------------------------------------------------12分
------------------------------------------------12分
又,要使直线![]() 与椭圆有两个交点,必须
与椭圆有两个交点,必须![]() 即
即
![]() ⑤ 而
⑤ 而![]() 满足⑤
满足⑤
∴存在![]() ,使得点Q在以CD为直径的圆上----------------14分。
,使得点Q在以CD为直径的圆上----------------14分。