高三数学调研试题3
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分.考试时间120分钟
第Ⅰ卷（选择题共60分）
一.选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的.
1、某校高中生共有900人，其中高一年级300人，高二年级200人，高三年级400人，现采取分层抽样调查，抽取容量为45的样本，那么，高一，高二，高三各年级抽取人数分别为 （ ）
A．15，5， 25； B．15，15，15；
C．10，15，20； D．15，10，20.
2、已知向量
平行，则
等于 （ ）
A．－2 B．2 C．
D．
3、集合
映射
，在
作用下点
的象是
则集合
是
（ ）
A、
B、
C、 
D、
4、已知函数
，若在
上存在
，使
，则实数的取值范围是（ ）
A、
B、
C、[-1，2] D、[-2，1]
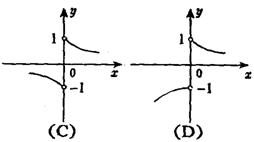
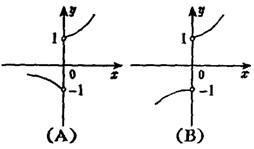
5、函数
的图象的基本形状是 （ ）
|
|
6、已知方程
的解为
，则属于（ ）
A、（3，4） B、（4，5） C、（5，6） D、（6，7）
7、已知
则下列各式正确的是（ ）
A．
B．
C．
D. 
8、若函数
在
内单调递减，则
可以是（ ）
A、
B、
C、
D、
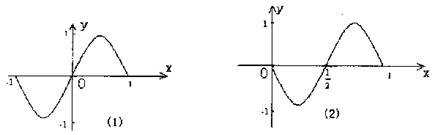
9、已知函数
的图象的一部分如图（1），则图（2）的函数图象所对应的函数解析式为 （ ）
|
A．
B．
C．
D．
10、已知函数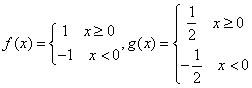
，则
在
处（
）
A．不连续 B．连续 C．不确定连续与否 D．以上答案都不正确
11、在等差数列
中，若
则
的值为（ ）
A．20 B．22 C．24 D．28
12、已知函数
（定义域为D，值域为A）有反函数
，则方程
有解
，且
的充要条件是满足（ ）
A、
B、
C、的图象位于
的下方 D、且与
轴的交点为（0，
）
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
13、已知
,则
；
14、按ABO血型系统学说，每个人的血型为A，B，O，AB四种之一，依血型遗传学，当且仅当父母中至少有一人的血型是AB型时，子女一定不是O型，若某人的血型为O型，则父母血型所有可能情况有 种；
15、已知关于
的方程
与
的解集都为空集，则实数的取值范围是________________；
16、设是定义域为
的一个函数，给出下列5个论断：
①的值域为；②是上的单调递减函数；
③是奇函数；④在任意区间
上的最大值为
，最小值为
；
⑤有反函数.
以其中某一论断为条件，另一论断为结论，如
② 
④ ，写出你认为正确的另两个命题：
⑴__________;⑵__________.
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.
17、（本小题满分12分）
已知向量
，设
.
（Ⅰ）求函数的最小正周期及最大值;
（Ⅱ）在给出的直角坐标系中，画出函数
在区间
上的图象．
18、（本小题满分12分）
我校高三级学生宿舍自主管理委员会共有五名楼长，其中2名女生，3名男生.学校为表扬先进，决定从这五名楼长选出3人进行表彰.设
表示选出的3名代表中女生楼长的个数.
求： 的概率分布及
.
19、（本小题满分12分）
已知函数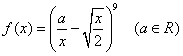
（Ⅰ）已知展开式中
的系数为
，求常数；
（Ⅱ）设
，若
在
内单调递增，求的取值范围
20、（本小题满分12分）
已知如图所示的数表，满足：
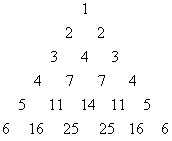①第
行
的首尾两个数都为；
②第行的其它的数类似于杨辉三角的性质.
⑴求：数表中第行的第二个数
；
⑵设
求证：
21．（本小题满分13分）
已知函数
（Ⅰ）若函数图像上任意一点切线的斜率小于1，求证：
；
（Ⅱ）若
，函数图像上任意一点切线的斜率为
，试讨论
的充要条件。
22、（本小题满分13分）
已知函数
，点
是函数图像上任意两点，且线段
中点
的横坐标为
.
（I）求证：的纵坐标为定值.
（II）若数列的通项公式为
，求数列的前项和.
（III）若
不等式
恒成立，求实数的取值范围.
高三调研试题
数 学 答题卡（2004.1.4）
| 班 级 |
| 三 （ ） |
| 姓 名 |
| 学 号 |
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.
17、（本小题满分12分）
已知向量，设
.
（Ⅰ）求函数的最小正周期和最大值.
（Ⅱ）在给出的直角坐标系中，画出函数在区间上的图象．
18、（本小题满分12分）我校高三级学生宿舍自主管理委员会共有五名楼长，其中2名女生，3名男生.学校为表扬先进，决定从这五名楼长选出3人进行表彰.设表示选出的3名代表中女生楼长的个数.
求： 的概率分布及.
19、（本小题满分12分）
已知函数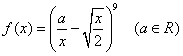
（Ⅰ）已知展开式中的系数为，求常数；
（Ⅱ）设，若在内单调递增，求的取值范围
20、（本小题满分12分）已知如图所示的数表，满足：
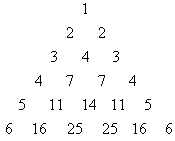①第行的第一个数和最后一个数都为；
②第行的其它的数类似于杨辉三角.
⑴求：数表中第行的第二个数；
⑵设求证：
21．（本小题满分13分）
已知函数
（Ⅰ）若函数图像上任意一点切线的斜率小于1，求证：；
（Ⅱ）若，函数图像上任意一点切线的斜率为，试讨论的充要条件。
| 班 级 |
| 三 （ ） |
| 姓 名 |
| 学 号 |
22、（本小题满分13分）
已知函数
，点是函数图像上任意两点，且线段中点的横坐标为.
（I）求证：的纵坐标为定值.
（II）若数列的通项公式为，求数列的前项和.
（III）若不等式
恒成立，求实数的取值范围.