高三数学调研试题4
数 学 答案及评分标准
一.选择题:本大题共12小题,每小题5分,共60分
![]()
二、填空题:本大题共4小题,每小题4分,共16分.
13、![]() 14、
14、![]() 15、
15、![]() 16、②
16、②![]() ⑤ ; ④
⑤ ; ④![]() ②
②
三、解答题:本大题共6小题,共74分
![]()
 17、(本小题满分12分)本题考查(1)三角函数基本变形及周期和最值的求法(2)利用五点法作图的能力
17、(本小题满分12分)本题考查(1)三角函数基本变形及周期和最值的求法(2)利用五点法作图的能力
解:(1)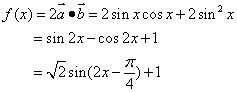 ┉┉┉┉5分
┉┉┉┉5分
![]() 函数最小正周期为
函数最小正周期为![]() ┉┉┉┉6分
┉┉┉┉6分
函数最大值为![]() .┉┉┉┉7分
.┉┉┉┉7分
(2)函数图像如右图.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉9分
(作图3分)
18、(本小题满分12分)本题考查概率分布与数学期望的知识及解决实际问题的能力.
解:![]() 的可能取值为
的可能取值为![]() .则
.则![]() ┉┉┉┉2分
┉┉┉┉2分
![]() ┉┉┉┉4分
┉┉┉┉4分 ![]() ┉┉┉┉6分
┉┉┉┉6分
|
|
|
|
|
|
|
|
|
|
故![]() 的概率分布为
的概率分布为
┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉8分
从而![]() ┉┉┉┉12分
┉┉┉┉12分
19、(本小题满分12分)本题考查(1)二项式定理的通项公式;(2)利用导数判断函数单调性.(3)函数思想,转化与化归的能力.
解:(1)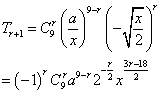 ┉┉┉┉2分
┉┉┉┉2分
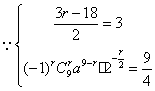 ,
,![]() ┉┉┉┉5分
┉┉┉┉5分
(2)![]() ,则
,则![]() ┉┉┉┉8分
┉┉┉┉8分
因为![]() 在
在![]() 内单调递增,则当
内单调递增,则当![]() 时恒有
时恒有![]()
![]() 亦
亦![]() 要使
要使![]()
在![]() 恒成立只须
恒成立只须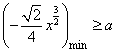 ┉┉┉┉┉11分
┉┉┉┉┉11分
故![]() ┉┉┉┉┉12分
┉┉┉┉┉12分
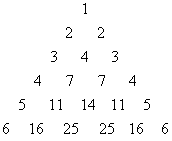
20、(本小题满分12分)本题考查(1)杨辉三角的的性质;(2)求递推数列通项的一般方法;(3)观察,放缩,归纳推理及分析问题解决问题的能力.
(1)由数表及杨辉三角的性质可知,![]()
┉┉┉┉┉2分
 故
故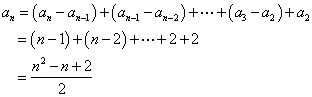 ┉┉┉┉6分
┉┉┉┉6分
(2)由![]() 则
则![]()
![]() (
(![]() ┉┉┉┉┉┉┉┉┉┉9分
┉┉┉┉┉┉┉┉┉┉9分
![]()
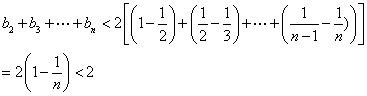 ┉┉┉┉┉┉┉┉12分
┉┉┉┉┉┉┉┉12分
21、(本小题满分13分)本题考查(1)导数的几何意义(2)恒成立问题中参数取值范围的求法.
(3)分析问题解决问题的能力.需要学生熟练掌握求最值的方法.
解:(1)依题意,由![]() ,则
,则![]() .┉┉┉┉┉┉┉┉2分
.┉┉┉┉┉┉┉┉2分
又函数![]() 图像上任意一点切线的斜率小于1,即
图像上任意一点切线的斜率小于1,即![]() 亦即
亦即![]() 对任意的
对任意的![]() 恒成立. 故
恒成立. 故![]() ,即
,即![]() ┉┉┉┉┉5分
┉┉┉┉┉5分
(2)由题可知,原问题等价于![]() 对
对![]() 恒成立. ┉┉┉┉7分
恒成立. ┉┉┉┉7分
当![]() 时,显然有
时,显然有![]() ,故当
,故当![]() 时
时 ![]() 从而
从而
![]() (※)对
(※)对![]() 恒成立. ┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉8分
恒成立. ┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉8分
令![]() .则可知
.则可知![]() 在
在![]() 上递增,故
上递增,故![]()
![]() ,当切仅当
,当切仅当![]() ,故
,故![]() ┉┉┉┉┉┉┉┉┉┉11分
┉┉┉┉┉┉┉┉┉┉11分
要使(※)恒成立只须![]() ,即
,即![]() 为
为![]() 在
在![]() 的充要条件
的充要条件
┉┉┉┉┉┉┉┉┉┉13分(其它解法酌情给分)
22、(本小题满分13分)本题考查(1)定值问题的处理的一般方法(2)观察、分析、类比及直觉思维(3)引导学生重视公式定理的推导过程.
解(1)依题意,![]() .┉┉┉┉1分
.┉┉┉┉1分
从而 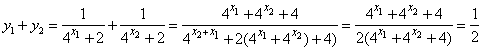
所以![]() 即
即![]() 点纵坐标也为定值. ┉┉┉┉4分
点纵坐标也为定值. ┉┉┉┉4分
(2)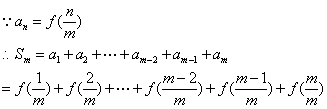
又![]()
则![]() ┉┉┉┉6分
┉┉┉┉6分
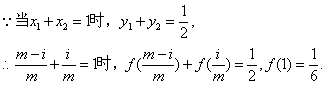 ┉┉┉┉8分
┉┉┉┉8分
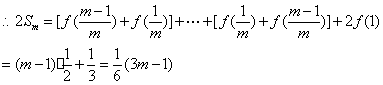
![]() .┉┉┉┉9分
.┉┉┉┉9分
(3)由![]() ,则
,则![]() ,即
,即![]() ,┉┉┉┉10分
,┉┉┉┉10分
故![]() 恒成立.若
恒成立.若![]() 命题不恒成立.从而
命题不恒成立.从而![]()
故![]() 恒成立.即
恒成立.即![]() .设
.设![]()
对于![]() ,可知
,可知![]() 为减函数.所以
为减函数.所以![]() ┉┉┉┉12分
┉┉┉┉12分
所以![]() ┉┉┉┉13分
┉┉┉┉13分