高三数学二轮复习第一次模拟测试题
一、选择题：
1、抛物线
上，横坐标为4的点到焦点的距离为5，则p的值为（ ）
(A)
(B) 1 (C) 2 (D)
4
2、两个完全相同的长方体的长、宽、高分别为5cm，4cm，3cm，把它们重叠在一起组成一个新长方体，在这些新长方体中，最长的对角线的长度是（ ）
(A)
(B)
(C)
(D)
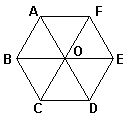
3、如图，点O是正六边形ABCDEF的中心，则以图中点A、B、C、D、E、F、O中的任意一点为始点，与始点不同的另一点为终点的所有向量中，除向量
外，与向量共线的向量共有（ ）
(A)4个 (B)7个 (C)8个 (D)9个
4、若
展开式中含有常数项，则正整数n的最小值是（ ）
(A) 4 (B) 5 (C) 6 (D) 8
5、已知在
中，
，
，
，则
（ ）
(A)
(B)
(C)
(D)或
6、若函数
的图像按向量
平移后，它的一条对称轴是
，则
的一个可能的值是（ ）
(A)
(B)
(C)
(D)
7、已知直线l、m，平面
、
，且
，
。给出四个命题：⑴若∥，则
；
⑵若,则∥；⑶若
，则l∥m；⑷若l∥m，则。其中正确的命题个数是（ ）
(A) 4 (B) 1 (C) 3 (D) 2
8、若是锐角，
,则
的值等于（ ）
(A)
(B)
(C)
(D)
9、在
中，有命题
①
；②
； ③若
，则为等腰三角形； ④若
，则为锐角三角形。上述命题正确的是（ ）
(A)①② (B)①④ (C)②③ (D)②③④
10、已知
，并且
是方程
的两根，实数a、b、、
的大小关系可能是（ ）
(A)
(B)
(C)
(D)
11、已知椭圆：
（
）的左、右焦点分别为
、
，以为顶点，为焦点的抛物线经过椭圆短轴的两端点，则椭圆的离心率为（ ）
(A)
(B)
(C)
(D)
12（理）、如果
，其中0＜p＜1，那么使
取最大值的k值（ ）
(A)有且有1个 (B)有且只有2个 (C)不一定有 (D)当
为正整数时有2个
12（文）、期中考试以后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M︰N为（ ）
(A)
(B)2 (C)
(D)1
二、填空题：
13（文）、根据下列5个图形及相应点的个数的变化规律，试猜测第
个图中有___________个点。
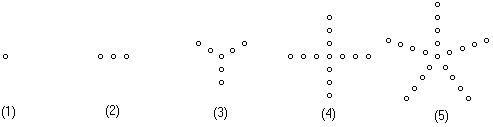
13（理）、复数
满足
，则的实部是__________。
14、在数列
中，
，且对任意大于1的正整数，点
在直线
上，则
_____________。
15、若直线
与圆
没有公共点，则m，n满足的关系式为___________；以
为点P的坐标，过点P的一条直线与椭圆
的公共点有_________个。
16、已知函数
满足：
，
，则
。
考号： 班级： 姓名： 成绩：
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
13： 14： 15： ； 16：
三、解答题：
17、某人忘记了电话号码的最后一个数字，因而他随意地拨号，假设在拨最后一个数字时拨过了的号码不再重复，试求下列事件的概率：
⑴第3次拨号才接通电话；
⑵拨号不超过3次而接通电话。
18、△ABC中，三个内角A、B、C的对边分别是a、b、c，若△ABC的面积为S，且
。求
的值。
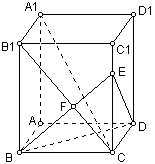19、已知长方体AC1中，棱AB＝BC＝3，棱BB1＝4，连结B1C，过B点作B1C的垂线交CC1于E，交B1C于F。
⑴求证A1C⊥平面EBD；
⑵求点A到平面A1B1C的距离；
⑶求平面A1B1CD与直线DE所成角的度数；
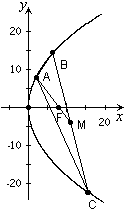20、如图：已知点
在抛物线上，
的重心与此抛物线的焦点F重合。
⑴求抛物线的方程和焦点F的坐标；
⑵求线段BC中点M的坐标；
⑶求BC所在直线的方程。
21、已知函数
，
（
为正常数），且函数
与
的图象在
轴上的截距相等。
⑴求的值；
⑵求函数
的单调递增区间；
⑶（理）若为正整数，证明：
（取
）。
22（理）、设
，
，若
。当
时，试求函数关系式
，并求函数在
上的最大值。
22（文）、已知平面向量
，
。
⑴求证：
；
⑵若存在实数k和t，使得
，
，且
。试求函数关系式
；
⑶根据⑵的结论，确定函数的单调区间。