高三数学二轮复习第一次模拟测试题参考解答
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | D | B | C | A | D | A | C | A | C | D |
13、(文)![]() (理)1 14、
(理)1 14、![]() 15、①
15、①![]() ②2 16、24
②2 16、24
17、解:用![]() 表示第
表示第![]() 次拨号接通电话,
次拨号接通电话,![]() 1,2,3。
1,2,3。
(1)第3次才接通电话可表示为![]() ,于是所求概率为
,于是所求概率为![]() ;
;
(2)拨号不超过3次而接通电话可表示为:![]() ,于是所求概率为
,于是所求概率为
![]() 。
。
18、依题意,得![]() 。由余弦定理知:
。由余弦定理知:![]() 。
。
∴![]() ,即
,即![]() 。
。
![]()
![]() 又
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ∴
∴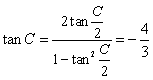 。
。
(方法二)由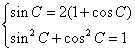 得
得![]() (舍)或
(舍)或![]()
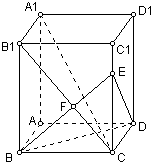 ∴
∴![]() 。
。
19、解:⑴连结AC,则![]() ,∵AC是A1C在平面ABCD内的射影
,∵AC是A1C在平面ABCD内的射影
∴![]() ;
;
∵![]() ,且A1C在平面
,且A1C在平面![]() 内的射影
内的射影![]()
∴![]() 又∵
又∵![]() ∴
∴![]()
⑵∵AB∥面![]() ∴即求点B到面
∴即求点B到面![]() 的距离。
的距离。
易证:BF⊥平面A1B1C, ∴所求距离即为![]()
⑶连结DF,A1D,∵![]() ,
,![]() ∴
∴![]() ,
,
∴∠EDF即为ED与平面A1B1C所成的角
由条件![]() ,
,![]() ,可知
,可知![]() ,
,![]() ,
,![]() ,
,![]() , 由
, 由![]() 得:
得:![]() ,
,![]()
∴![]() ∴
∴![]()
∴ED与平面A1B1C所成角为![]() 。
。
 20、解:⑴由点
20、解:⑴由点![]() 在抛物线
在抛物线![]() 上,得
上,得![]() 。
。
所以抛物线方程为![]() ,焦点F的坐标为
,焦点F的坐标为![]()
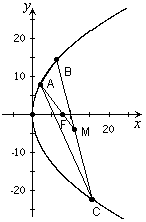
⑵如图,![]() 是
是![]() 的重心,M是BC的中点
的重心,M是BC的中点
∴F是线段AM的定比分点,且![]()
设点M的坐标为![]() ,则
,则
![]() 解得
解得![]()
所以点M的坐标为![]()
⑶由于线段BC的中点M不在x轴上,所以BC所在的直线不垂直于x轴。
设BC所成直线的方程为 ![]()
由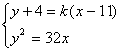 消x得
消x得 ![]()
所以![]() 由(Ⅱ)的结论得
由(Ⅱ)的结论得![]() 解得
解得![]()
∴直线BC的方程为![]() 即
即![]()
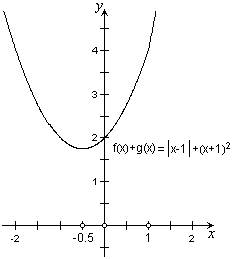
21、⑴由题意,![]() ,
,![]() ∵
∵![]() ,∴
,∴![]() 。
。
⑵![]()
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增。
上单调递增。
∵函数![]() 在
在![]() 处连续
处连续
∴单调区间为![]() 。
。
⑶设![]() ,考查数列
,考查数列![]() 的变化规律:
的变化规律:
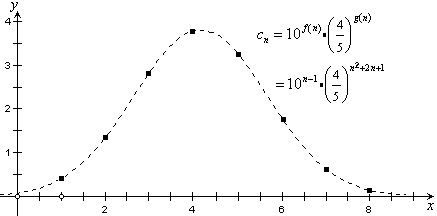
解不等式![]() ,由
,由![]() ,上式化为
,上式化为![]()
解得![]() ,因
,因![]() 得
得![]() ,于是
,于是![]() ,而
,而![]()
所以![]() 。
。
(方法二)要证![]() ,只需证
,只需证![]()
即证![]() ,由
,由![]() 得:只需证
得:只需证![]()
22、(文)⑴证明:∵![]() ∴
∴![]()
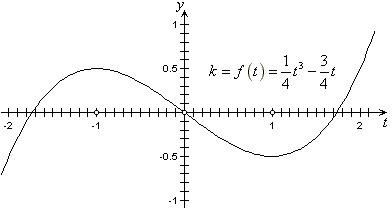 ⑵解:由题意知
⑵解:由题意知![]() ,
,![]()
∵![]() ∴
∴![]()
整理得:![]() ∴
∴![]()
(3)解:由 ![]() 得
得 ![]()
令 ![]() 得
得 ![]() ;令
;令 ![]() 得
得 ![]() 或
或 ![]()
∴函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() 。
。
22(理)、解:∵![]() ∴
∴![]()
∴![]() 。令
。令 ![]() 得
得 ![]()
当![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 上是增函数 ∴最大值为
上是增函数 ∴最大值为![]() ;
;
当![]() 时,由
时,由![]() 得
得![]() ∴
∴![]()
∴①当![]() 时,
时,![]() 。由
。由![]() 得
得![]() ∴
∴![]()
∴![]() ∴函数
∴函数![]() 在
在![]() 上是增函数 ∴最大值为
上是增函数 ∴最大值为![]() ;
;
②当![]() 时,由
时,由![]() 得
得![]() ,且
,且![]()
这时在![]() 上
上![]() ;在
;在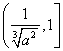 上
上![]()
∴函数![]() 在
在![]() 上是增函数,在
上是增函数,在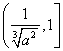 上是减函数
上是减函数
∴最大值为 ![]()
 综上可得:当
综上可得:当![]() 时最大值为
时最大值为![]() ;
;
当![]() 时最大值为
时最大值为![]() 。
。