高三数学模拟试卷（一）
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P（A+B）=P（A）+P（B） S=4πR2
如果事件A、B相互独立，那么 其中R表示球的半径
P（A·B）=P（A）·P（B） 球的体积公式
如果事件A在一次试验中发生的概率是P，
那么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．（改）一个圆的圆心在原点，并且与直线 4x+3y+5=0 相切，则这个圆的方程为 （ ）
A．x2+y2=5 B．x2+y2=25 C．x2+y2=1 D． x2+y2=2
2．（新）在△ABC中，tanA·tanB=tanA+tanB+1，则角C为 （ ）
A．45º B．135º C．150º D．30º
3．（改）已知m，n是方程lg2x+lg15lgx+lg3lg5=0的两根，则mn的值为 （ ）
A．-(lg3+lg5) B．lg3lg5 C．
D．
4．（改）若x、y
R，则x<1且y<1是 x+y+x- y<2成立的
（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．不充分不必要条件
5．（新）一个凸多面体，各面都是五边形，且从每个顶点出发有3条棱，则该多面体（ ）
A．不一定是十二面体 B．只能是十二面体
C．不存在这样的多面体 D．只能是正十二面体
6．（新）一次测试由12道选择题构成，每题选择正确得5分，不选或错选得零分，满分得60分，某学生选对任一题的概率是0.8，则该学生在这次测试中成绩的期望和方差分别是 （ ）
A．48、1.92 B．48、0.16 C．48、2.4 D．24、2.4
7．（改）设P={x1，x2，x3}是方程x3=1在复数集C中的解集，M={x1x2，x2x3，x3x1}，则P与M的关系是 （ ）
A．PÍM B．PÊM C．P = M D．P∩M =
8．（改）函数
的图象的相邻两支截直线y=1所得线段长为
，则
的值是 （ ）
A． -1 B．1 C．0 D．
9．（改）不等式组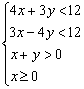
所表示的平面区域内的整点(横坐标和纵坐标都是整数的点)个数是
（ ）
A．7 B．9 C．10 D．11
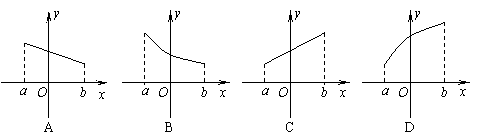10．（新）任取x1、x2∈[a，b]且x1≠x2，若f(
)＞
[f(x1)+f(x2)]，则f(x)在[a，b]上是上凸函数．在以下图象中，是上凸函数的图象是
（ ）
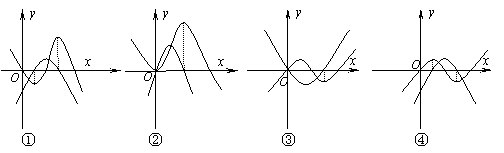11．（新）以下四图，都是同一坐标系中三次函数及其导函数的图象，其中一定不正确的序号是
（ ）
A．①② B．③④ C．①③ D．①④
12．（新）若双曲线y2-x2=1与
有唯一的公共点，则实数m的取值集合的元素个数为
（ ）
A．2 B．4 C．5 D．6
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．
13．（改）长方形ABCD与长方形CDEF所在两平面互相垂直，设AF与平面BD所成的角为a，AF与CD两异面直线的角为b，且AB、BC、CF的长分别为4、3、2，则cosacosb的值为 ．
14．（改）将一张建有坐标系的坐标纸折叠一次，使得点（1，0）与点（-1，2）重合，且点（6，1）与点（m，n）重合，则m+n的值是
．
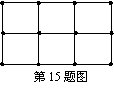
15．（改）从图中（3×2个小正方形围成的矩形）的12个点中任取3个点，可组成三角形的个数是 ．
16．（新）设a为一非零实数，则方程x3+x2-x+a=0．
① 有三个负根；②有二个负根和一个正根；
③有一个负根和二个正根；④有三个正根；⑤仅有一个实根．
以上情形可能成立的有 ．
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（改）（本小题满分12分）
已知平面上三个不同向量a、b、c的模相等，且它们相互之间的夹角均为120º．
（Ⅰ）求向量a- b与向量c的夹角；
（Ⅱ）若ka+b+c ＞a+b （k∈R），求k的取值范围．
18．（改）（本小题满分12分）
甲、乙两人约定在上午7时到8时之间在某地会面，并约定先到者应等候另一个人一刻钟，过时即可离去．求两人能会面的概率．
19．（新）（本小题满分12分）
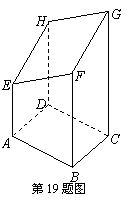如图是表示以AB=4，BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体，其中四边形EFGH为截面．已知AE=5，BF=8，CG=12．
（Ⅰ）作出截面EFGH与底面ABCD的交线l；
（Ⅱ）截面四边形EFGH是否为菱形？并证明你的结论；
（Ⅲ）求DH的长；
（Ⅳ）求截面EFGH与底面ABCD所成锐角的余弦值．
20．（新）（本小题满分12分）
已知一个数列{an}的各项是1或3．首项为1，且在第k个1和第k+1个1之间有2k-1个3，即1，3，1，3，3，3，1，3，3，3，3，3，1，…．记数列的前n项的和为Sn．
（Ⅰ）试问第2004个1为该数列的第几项？
（Ⅱ）求a2004；
（Ⅲ）S2004；
（Ⅳ）是否存在正整数m，使得Sm=2004？如果存在，求出m的值；如果不存在，说明理由．
21．（改）（本小题满分12分）
已知曲线y=ax3-bx（a≠0）上有两不同的点A、B，且过A、B两点的切线都垂直于直线AB．
（Ⅰ）试判断A、B两点是否关于原点对称，并说明理由；
（Ⅱ）求出a、b所满足的条件，并画出点P(a，b)的存在范围．
22．（新）（本小题满分14分）
已知集合M是满足下列性质的函数f(x)的全体：存在非零常数k，对任意x∈D(D为函数的定义域)，等式f(kx)=
+f(x)成立．
（Ⅰ）一次函数f(x)= ax+b（a≠0）是否属于集合M？说明理由；
（Ⅱ）设函数f(x)=
（a＞1）的图象与y=x的图象有公共点，试证明：
f(x)=∈M．
高三数学综合试卷（一）答案
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．C（点拨：圆的半径等于原点到直线的距离，等于1）
2．A（点拨：
ÞA+B=135ºÞC=45º）
3．D（点拨：方程的两根分别为
、
）
4．C（点拨：易推得当x<1且y<1时，有 x+y+x- y<2；另一方面，x+y+x- y<2Ûx2+y2+x2- y2<2。若x≤y，则y<1，从而x<1；若y≤x，则x<1，从而y<1）
5．Ｂ（点拨：V+F- E=2，且5F=2E=3V）
6．A（点拨：期望为5np=48，方差= npq=1.92）
7．C（点拨：P={1，ω，ω2}，M={ω，ω2，ω3}，注意ω3=1，其中
）
8．Ｃ（点拨：周期T=，ω=
=4，f(x)=tan4x）
9．B（点拨：在直角坐标系内作出不等式组所表示的平面区域）
10．D（利用数形结合法，在图示中分别作出f()与[f(x1)+f(x2)]，并比较它们的大小）
11．B（点拨：导函数的图象是抛物线，导函数的值大于0，原函数为增函数）
12．D（点拨：后者方程为直线l且除去其上的两点A、B，当l平行于双曲线的渐近线或l与双曲线相切或双曲线过l上一点与点A或B时，两曲线均只有一个公共点，每种情况下各有两解）
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．
13．
14．7 15．200 16．②③⑤
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（Ⅰ）依题意，三个向量的模不能为零，故可设a = b = c = r＞0，又a、b、c之间的夹角均为120º，于是
(a-b)·c = a·c-b·c = a·ccos120º- b·ccos120º = 0，
故 向量a-b与向量c的夹角为90º．
（Ⅱ）因ka+b+c＞a- b ，故ka+b+c2＞a+b 2，
即 (ka+b+c)·(ka+b+c)＞(a+b)·( a+b)，也就是
k2a·a+b·b+c·c+2ka·b+2ka·c+2b·c＞a·a+b·b+2a·b．
因 a·b = a·c = b·c = r2cos120º= 
r2，a·a=b·b= r2，
故 k2-2k＞0，解得k＜0或k＞2．
18．以x和y分别表示甲、乙两人到达约会地点的时间，则两人能够会面的充要条件是
≤15．在平面上建立直角坐标系如图，则(x，y)的所有可能结果是边长为60的正
方形，而可能会面的时间由图中的阴影部分所表示．故
．
19．（Ⅰ）如图，作HE与AD的交点P，作GF与BC的交点Q，连PQ得直线l，它便是所求作．
（Ⅱ）截面EFGH为菱形．
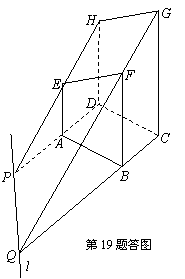因平面ABFE∥平面DCGH，且平面EFGH分别截平面ABFE与平面DCGH得直线EF与GH，故EF∥GH．
同理，FG∥EH，故四边形EFGH为平行四边形．
又EF2=AB2+(BF-AE)2=25，FG2=BC2+(CG-BF)2=25，于是EF=FG=5，
故 四边形EFGH为菱形．
（Ⅲ）由AE+CG=BF+DH，得 DH=9．
（Ⅳ）FH2=BD2+(DH-BF)2=26，
EG2=AC2+(CG-AE)2=74，
故菱形EFGH的面积为
SEFGH =
．
又SABCD =
，
由面积射影定理得，所求锐角的余弦为
．
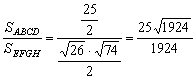20．将第k个1与第k+1个1前的3记为第k对，即（1，3）为第1对，共1+1=2项；（1，3，3，3）为第2对，共1+（2×2-1）=4项；
为第k对，共1+（2k-1）=2k项；…．故前k对共有项数为
2+4+6+…+2k=k(k+1)．
（Ⅰ）第2004个1所在的项为前2003对所在全部项的后1项，即为
2003(2003+1)+1=（项）．
（Ⅱ）因44×45=1980，45×46=2070，故第2004项在第45对内，从而a2004=3．
（Ⅲ）由（Ⅱ）可知，前2004项中共有45个1，其余1959个数均为3，于是
S2004=45+3×1959=5922．
（Ⅳ）前k对所在全部项的和为
Sk(k+1)=k+3[k(k+1)-k]=3k2+k．
易得，S25(25+1)=3×252+25=1900，S26(26+1)=3×262+26=2054，S651=1901，且自第652项到第702项均为3，而2004-1901=103不能被3整除，故不存在m，使Sm=2004．
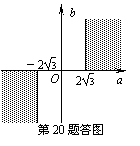21．（Ⅰ）y¢=3ax2 –b．设A(s，as3-bs)、B (t，at3-bt)为曲线上两不同的点，从而s≠t．依题意有，过A、B两点切线的斜率相等（或都不存在），从而3as2-b=3at2-b．由于a≠0，故s2=t2，于是s = - t，即A、B两点关于原点对称．
（Ⅱ）
．
依题意as2·(3as2-b)= -1，即3a2(s2)2-abs2+1=0．
令x=s2，则方程3a2x2-abx+1=0至少有一个正根．因方程两根之积为 ＞0，故方程两根均为正根，从而两根之和 ＞0，且△= (ab)2-12a2≥0．于是，a、b同号，且b2≥12，图象如图所示．
22．（Ⅰ）若一次函数f(x)∈M，即存在非零常数k，使得等式akx+b=+ ax+b，也就是a(k-1)x=成立．显然对于任意x∈D=R，a(k-1)x=不能恒成立，故f(x)= ax+bÏM．
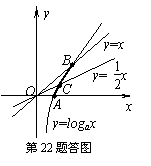（Ⅱ）如图，设函数f(x)=（a＞1）的图象与函数y=x的图象的公共点为B(t，t)，则显然t＞1．在x∈(1，t)上，函数f(x)=（a＞1）有定义，故在函数f(x)=（a＞1，x∈(1，t)）的图象即弧AB上，必存在点C（k，），使等式
成立，其中1＜k＜t．
于是，f(kx)=
，故f(x)=∈M．