高三数学模拟试题

高三数学模拟试题

参考公式：三角函数和差化积公式：

　　

　　

第Ⅰ卷（选择题，共60分）

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知，则在上的射影为　　　　　　　　　　　　　

　　（A） ；　　　 （B） ；　　　　（C） ；　　　　（D）

2.给出如下几个变换：①横坐标伸长到原来的2倍，纵坐标不变. ②横坐标缩短到原来的倍，纵坐标不变．③向左平行移动3个单位长度. ④向右平行移动3个单位长度. ⑤向左平行移动个单位长度.则由函数的图象得到的图象，可实施的方案为(　)

A．①®③  B．②®③ 　 C．②®④　 　 D．②®⑤

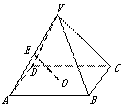
3.如图，已知正四棱锥的侧棱长与底面边长相等，是的中点，是底面中心，则异面直线与所成的角是(　)

A． 　 B．　　C． 　 D．

4.若是实数，则是的(　)

A．充分非必要条件　　B．必要非充分条件

C．充要条件　 D．既非充分也非必要条件

5.正方体的直观图如图所示，则其展开图是(　)

6．若a＝2＋i，则1－C的值为
A.－2⁸　　　　　　　　B.2⁸　　　　　　　　C.(3－i)¹⁶　　　　　 D.(3＋i)¹⁶

7．将一张建有坐标系的坐标纸折迭一次，使得点（1，0）与点（－1，2）重合，点（6，1）与点（m，n）重合，则m+n的值是(　)　　　　　　　　　　　　　　

　　A．6 　　　B．7 　　　C．8 　　　　D．9

8．某商场对顾客实行购物优惠活动，规定一次购物付款总额：

　　①如果不超过200元，则不予优惠②如果超过200元但不超过500元，则按标价给予9折（即标价的90%）优惠③如果起过500元，其500元按第②条给予优惠，超过500元的部分给予7折优惠。某人两次去购物，分别付款168元和423元，假设他只去一次购买上述同样的商品，则应付款是（　）

　　A．413.7元　　　B．513.7元　　　C．546.6元　　　 D．548.7元

9．甲、乙、丙、丁四人相互传球，第一次甲传给乙、丙、丁三人中任一人，第二次由拿球者再传给其他三人中任一人，这样共传了4次，则第4次仍传回到甲的方法共有（　　）

 A．21种　　　B．24种　　　C．27种　　　 D．42种

10．函数的图象是　　　　　　　　　　　　　　　　 （　　）

　　

	A　　　　　　　　　　　  B　　　　　　　　　　　　　　  C　　　　　　　　　　　　 D

11．已知椭圆为参数），点P是时对应的点，则直线OP的倾斜角为（O为坐标原点）　　　　　　　　（　）　　　　　

A．　　 B．　　　　 C．　　　　D．

12．已知等差数列的前n项和为，若等于　　　（　　） A．18 　　　　 B．36　　　　 C．54 　　　　　　 D．72

二、填空题：本大题共4个小题；每小题4分，共16分，把答案填在题中横线上。

13．小军中午放学回家自己煮面条吃。有下面几道工序：①洗锅盛水2分钟；②洗菜6分钟；③准备面条及佐料2分钟；　④用锅把水烧开10分钟；  ⑤煮面条和菜共3分钟。以上各道工序，除④之外，一次只能进行一道工序。小军要将面条煮好，最少用　 　　　分钟.　　　　　　　　　　　 

14．已知函数的图象与的图象关于直线，则关于函数h（x）有下列命题：

①h（x）的图象关于原点（0，0）对称；　 ②h（x）的图象关于y轴对称；③h（x）的最小值为0；　　　　　  ④h（x）在区间（－1，0）上单调增。其中正确的命题是　　　　　

　　　　　　　　　　　　  　 

15．半径为R的三个球两两外切，放在桌面上，与这三个球都外切的小球也放在桌面上，则第四个小球的半径为_____________.

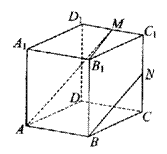
16．如右图，正方体ABCD—A₁B₁C₁D₁中，M、N分别为棱C₁D₁、C₁C上的中点，有以下四个结论：①直线AM与CC₁是相交直线②直线AM与NB是平行直线③直线BN与MB₁是异面直线④直线AM与DD₁是异面直线,.其中正确的结论为　　　 　

一．选择题答题卡

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二．填空题答题处：

13　　 　　　　　　　　 14　　　　　　  15　　　　　　  　16 　　　　　　　

三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.

17．（本小题满分12分）在△ABC中，三个内角A、B、C的对边分别为a、b、c，且角A为80°，，求角C的度数.

18．（本小题满分12分）排球比赛的规则是5局3胜制，A、B两队每局比赛获胜的概率都相等且分别为和.（Ⅰ）前2局中B队以2:0领先，求最后A、B队各自获胜的概率；

（Ⅱ）B队以3:2获胜的概率．

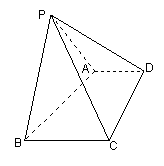
19.（本小题满分12分）如图：已知四棱锥P—ABCD的底面为直角梯形，AD∥BC，∠BCD=90，PA=PB，PC=PD.

　　　 （Ⅰ）证明CD与平面PAD不垂直；

　　　 （Ⅱ）证明平面PAB⊥平面ABCD；

　　　 （Ⅲ）如果CD=AD+BC，二面角P—BC—A等于60°，求二面角P—CD—A的大小．

20．(本小题满分12分）现有A、B、C、D四个长方体容器，容器A、B的底面积均为x²，高分别为x，y；容器C、D的底面积均为y²，高也分别为x，y（其中x≠y）。现规定一种两人的游戏规则：每人从四种容器中取两个盛水，盛水多者为胜。问先取者在末能确定x、y的大小的情况下有设有必胜的可能？若有的话，有几种方案？

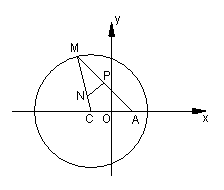
21.（本小题满分12分）如图所示，已知圆为圆上一动点，点P在AM上，

点N在CM上，且满足的轨迹为曲线E.

（I）求曲线E的方程；

（II）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），

　　 且满足，求的取值范围.

22.（本小题满分14分）已知数列｛a_n｝为等差数列，公差d≠0，由｛a_n｝中的部分项组成的数列a_b1，a_b2，…，a_bn,…为等比数列，其中b₁=1，b₂=5，b₃=17

（Ⅰ）求数列｛b_n｝的通项公式；

（Ⅱ）记

参考答案

一、选择题：本题考查基本知识和基本运算.每小题5分，满分60分.

1．c 2．D 3．C 4．B 5．D　6．B 7．B  8．C  9．A  10．B  11．A  12．D

二、填空题：本题考查基本知识和基本运算.每小题4分，满分16分.

13． 15　　14．②④　　15．　n(n+1)/2　 16．③④

三、解答题

20、解：依题意可知：A、B、C、D四个容器的容积分别为x³、x²y、xy²、x³。按照游戏规则，先取者只有三种不同的取法：①取A、B（或C、D）；②取A、C（或B、D）；③取A、D（或B、C）。实际上就是比较容器两两和大小。（3分）

　　方案①：(x³+x²y)－(xy²+y³)=x²(x+y)－y²(x+y)=(x－y)(x+y)²，显然(x+y)²＞0，而x与y的大小不确定，∴(x³+x²y)与(xy²+y³)的大小不能确定，即这种取法无必胜的把握。（6分）

　　方案②：(x³+xy²)－(x²y+y³)=x(x²+y²)－y(x²+y²)=(x－y)(x²+y²)，类似方案①，x与y的大小不确定，(x³+xy²)与(x²y+y³)的大小不能确定，即这种取法无必胜的把握。（9分）

方案③：(x³+y³)－(x²y+xy²)= (x+y)(x－y)²，显然(x+y)(x－y)²＞0，∴(x³+y³)＞(x²y+xy²)，故先取容器A、D是唯一必胜的方案。(12分)

22.解：（I）依题意

d≠0　 a₁=2d,数列{a_n}公比

　（4分）

又　　 

　 （6分）

（II）C+C+…+C=C（2·3⁰-1）+C（2·3¹-1）+…+C（2·3^n-1-1）

=［C·3+C·3²+…+C·3ⁿ］-(C+C+…+C)

=［（1+3）ⁿ-1］-(2ⁿ-1)= ·4ⁿ-2ⁿ+ （10分）

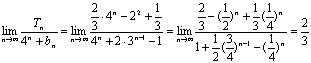（ 14分）

18．解:（Ⅰ）设最后A获胜的概率为设最后B获胜的概率为

　

　　　　 

（Ⅱ）设B队以3:2获胜的概率为．

21．解：（1）∴NP为AM的垂直平分线，∴NA=NM.

又

∴动点N的轨迹是以点C（－1，0），A（1，0）为焦点的椭圆.

且椭圆长轴长为焦距2c=2.　

∴曲线E的方程为

（2）当直线GH斜率存在时，

设直线GH方程为

得

设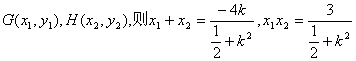

，

 

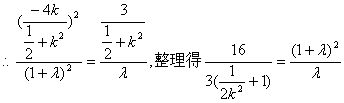
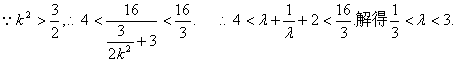
又当直线GH斜率不存在，方程为

19．解：(Ⅰ)若CD⊥平面PAD，则CD⊥PD，由已知PC=PD，得

∠PCD=∠PDC， 这与CD⊥PD矛盾，所以CD与平面PAD不垂直.

(Ⅱ)取AB、CD的中点E、F，连接PE、PF、EF，由PA=PB，PC=PD，得PE⊥AB，

PF⊥CD，∴EF为直角梯形的中位线，∴EF⊥CD，又PF∩EF=F,∴CD⊥平面PEF，由PE平面PEF，得CD⊥PE，又AB⊥PE且梯形两腰AB、CD必交，∴PE⊥平面ABCD，又PE平面PAB，∴平面PAB⊥平面ABCD

（Ⅲ）由（Ⅱ）及二面角的定义知∠PFE为二面角P-CD-A的平面角作EG⊥BC于G，连PG，由三垂线定理得BC⊥PG，故∠PGE为二面角P-BC-A的平面角．

　　即∠PGE=60°，由已知，得，又EG=CF=CD.∴EF=EG,易证得Rt⊿PEF≌Rt⊿PEG.∴∠PEF=∠PGE=60°，即为所求.