高三数学培优训练（二）
1、若集合A和B各含6个元素，A∩B含有3个元素，C同时满足两个条件：
①C
A∪B且C中含有3个元素；②C∩A≠
，则这样的集合C的个数是（ ）
A．82 B．83 C．84 D．219
2、下列各组命题中，满足“p或q”为真，“p且q”为假，“非p”为真的是（ ）
A．p：0=；q：0∈
B．p：在△ABC中，若cos2A=cos2B，则A=B；q：y=sinx在第一象限是增函数
C．p：a+b≥2
（a，b∈R）；q：不等式x＞x的解集为（－
，0）
D．p：y=2sinx＞2；q：y=3sinx(tanxtan
)的最小正周期为
3、已知数列
的通项公式
，设其前
项和为
，则使
成立的自然数
（ ）
A．有最小值63 B．有最大值63 C．有最小值31 D．有最大值31
4、等比数列{a n}中，a1=512，公比q=
，用
表示它的前项之积：
…
，
则
，…，中最大的是 （ ）
A．
B．
C．
D．
5、设
5、已知函数f(x)=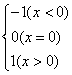
, 则
(a≠b)的值应为( )
A a B b C a, b之中较少的数 D a, b 之中较大的数
6、已知
，
，
是三个非零向量，命题
，命题
，则
是
的（ ）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件
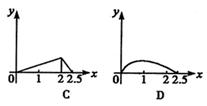
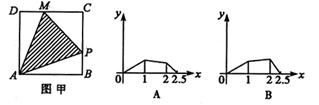
7、如图甲所示，点P在边长为1的正方形边上运动，设M是CD的中点，则当P沿A—B—C—运动时，点P经过的路程x为自变量，△APM的面积为y的函数，则
的图象形状大致是（ ）
|
|
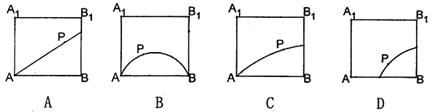
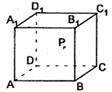
8、如图所示，在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC 的距离相等，则动点P所在曲线形状为（ ）
|
9、抽象函数是由特殊的、具体的函数抽象而得到的.如正比例函数
，
可抽象为
写出下列抽象函数是由什么特殊函数抽象而成（每项填入一个函数即可）.
| 特 殊 函 数 | 抽 象 函 数 |
|
| |
|
| |
|
|
10、下列命题：①动点M至两定点A、B的距离之比为常数
.则动点M的轨迹是圆.
②椭圆
为半焦距）③双曲线
的焦点到渐近线的距离为b ④已知抛物线
且OA⊥OB（O为原点）.则
。 其中正确的序号是
。
11、某种电热器的水箱盛水是200升，加热到一定温度即可浴用.浴用时，已知每分钟放水34升，在放水的同时按10.9毫升/ 秒2的匀加速度作自动注水（即t分钟自动注水2t2升），当水箱内的水量达到最小值时，放水自动停止.现假定每人洗浴用水量为65升，则该热器一次至多可供 人洗浴。
12、解不等式：
13. 某工厂有216名工人接受了生产1000台GH型高科技产品的总任务，已知每台GH型产品由4个G型装置和3个H型装置配套组成. 每个工人每小时能加工6个G型装置或3个H型装置. 现将工人分成两组同时开始加工，每组分别加工一种装置. 设加工G型装置的工人有
人，他们加工完G型装置所需时间为
，其余工人加工完H型装置所需时间为
（单位：小时，可不为整数）.（Ⅰ）写出
解析式；（Ⅱ）比较与的大小，并写出这216名工人完成总任务的时间
的解析式；（Ⅲ）应怎样分组，才能使完成总任务用的时间最少？
14.已知一次函数的图象关于直线
对称的图象为C，且
若点
）在曲线C上，并有
.
（Ⅰ）求的解析式及曲线C的方程；（Ⅱ）求数列{}的通项公式；
（Ⅲ）设
的值.
高三培优训练（二）参考答案
1、B 2、C 3 、A 4、C 5、D 6、D 7、A 8、C
9、见表 10、①②③ 11、 4
| 特 殊 函 数 | 抽 象 函 数 |
| 指数函数 |
|
| 对数函数 |
|
| 正切函数 |
|
12、定义域
且
，这时原不等式化为
分三种情况：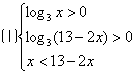
；
；
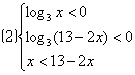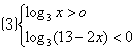
得解集为：
13.
13. 解：（Ⅰ）由题意知，需加工G型装置4000个，加工H型装置3000个，
所用工人分别为人，
人.
即
（Ⅱ）
当
；
当
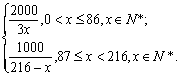
（Ⅲ）完成总任务所用时间最少即求的最小值.
当
时，递减，
此时
当
时，递增，
此时
∴加工G型装置，H型装置的人数分别为86，130或87，129.
14. 解：（Ⅰ）设
即
① 又
是曲线C的解析式，
因为点
在曲线C上，所以
，
又
代入①得
曲线C的方程是
。
（Ⅱ）由（Ⅰ）知当
时，
于是
（Ⅲ）因为
所以
所以