高三数学培优训练(一)
1、设集合
，则集合
的子集的个数是： A．11 B．10 C．15 D．16
2、已知：函数
＝
，
R,且
，
，
，则
的值
A．一定大于0 B.一定小于0 C.一定等于0 D.正负都有可能
3、在ΔABC中，∠A＝60°，
＝1，这个三角形的面积为
，则ΔABC外接圆的直径是
A．3
B.
C. 
D.
4、已知：
的反函数是
，将
的图像向左平移2个单位，再关于x轴对称后所得到的函数的反函数是
A．
B. 
C. 
D. 
5、奇函数
满足
，则
：
A．11 B．－11 C．2 D．－2
6、一个学生通过某种英语听力测试的概率是1/2，他连续测试n次，要保证他至少有一次通过的的概率大于0.9，那么他测试的次数n的最小值为：
A．3
B．4
C．5
D．6
7、已知函数
，则函数
的最大值是：
A．
B．
C．
D．
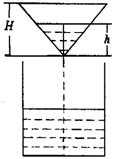
8、如图，液体从一个圆锥形漏斗漏入一圆柱桶中，开始时漏斗盛
满液体，经过3秒漏完，圆柱桶中液面上升速度是一个常量，则漏
斗中液面的高度
与下落时间
的函数关系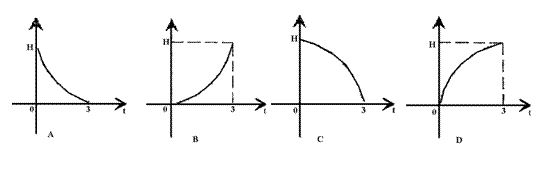
的图像只可能是：
9、二项式
的展开式中的第六项是63，而第三项的二项式系数
是21，则
.
10、已知铜的单晶体的外形是简单几何体，单晶体有三角形和八边形两种晶面，如果铜的单晶体有24个顶点，每个顶点处有3条棱，那么单晶铜的三角形晶面和八边形晶面的数目分别为 和 。
11、给定
，定义使
……
为整数的数
叫做企盼数，则区间〔1，2004〕内的所有企盼数的和M＝
。
12、在某次数学测验中，学号为
的四位同学的考试成绩
且满足
，则四位同学的考试成绩的所有可能情况有 种（用数字作答）.
13、记
＝（
），
＝（
），且0
（1）若向量与的夹角为锐角，求实数x的取值范围。（2）若//，且
，求实数
。
14、已知函数
，
（
为正常数），且函数
与
的图象在
轴上的截距相等。（1）求的值； （2）求函数
的单调递增区间；
（3）若
为正整数，证明：
.
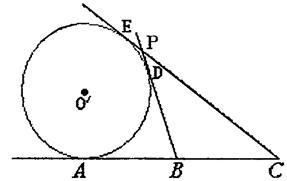
15、已知A、B、C是直线m上的三点，且AB=BC=6，⊙O′切直线m于点A,又过B、C作⊙O′异于
的两切线，切点分别为D、E，设两切线交于点P，（1）求点P的轨迹方程
（2）经过点C的直线与点P的轨迹交于M、N两点，且点C分
所成比等于2∶3，
|
的方程.
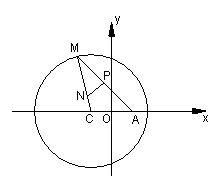
16、如图所示，已知圆
为圆上一动点，点P在A上，
点N在CM上，且满足
的轨迹为曲线E.（I）求曲线E的方程；（II）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），
且满足
，求的取值范围.
高三培优训练(一)参考解答
1——8： DBDA BBDC
9、
10、8,6 11、
12、15
13、(1)
(2) －2或1
14、(1)由题意，
，
又
，所以
(2)
………5分
当
时，
，它在
上单调递增；
当
时，
，它在
上单调递增。
(3)设
，对于数列
，解不等式
，由
，上式化为
，解得
。因
得
，于是
，
而
所以
。
15、（1）
点轨迹是B，C为焦点，长轴长等于18的椭圆.
以B，C两点所在直线为x轴，线段BC的垂直平分线为y轴建立直角坐标系.
则可设椭圆的方程是
点的轨迹方程是
（2）设
，
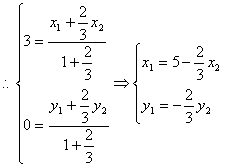
①
又
② 由①、②消去
解得
∴由C、N可得直线的方程是：
16．解：（1）
∴NP为AM的垂直平分线，∴NA=NM.
又
∴动点N的轨迹是以点C（－1，0），A（1，0）为焦点的椭圆.
且椭圆长轴长为
焦距2c=2. 
∴曲线E的方程为
（2）当直线GH斜率存在时，
设直线GH方程为
得
设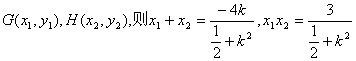
，
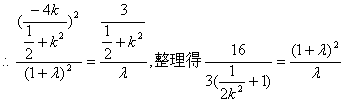
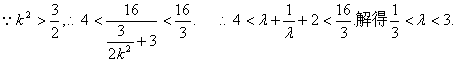
又当直线GH斜率不存在，方程为
