高三数学第二次模拟测试
本试卷分第I卷(选择题)和第II卷(非选择题)两部分，共150分。考试用时120分钟。
一、选择题(本大题共12小题，每小题5分，共60分，在每小题所给出的四个选项中，只
有一项是符合题目要求的)
1.直线
的倾斜角的取值范围是 ( )
A. 
B.
C.
D.
2.设方程
的根为α，[α]表示不超过α的最大整数，则[α]是 ( )
A．1 B．2 C．3 D．4
3.若“p且q”与“p或q”均为假命题,则 ( )
A.命题“非p”与“非q”的真值不同 B.命题“非p”与“非q”至少有一个是假命题
C.命题“非p”与“q”的真值相同 D.命题“非p”与“非q”都是真命题
4.设1！，2！，3！，……，n！的和为Sn，则Sn的个位数是 ( )
A．1 B．3 C．5 D．7
5.有下列命题①
＝
；②(
)＝
；③若
＝(
,4),则＝
的充要条件是＝
；④若
的起点为
,终点为
,则
与
轴正向所夹角的余弦值是
,其中正确命题的序号是 ( )
A.①② B.②③
C.②④ D.③④
6.右图中,阴影部分的面积是 ( )
A.16 B.18 C.20 D.22
图1
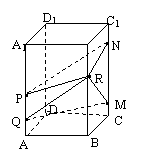
7.如图，正四棱柱ABCD–A1B1C1D1中，AB=3，BB1=4.长为1的线 图2
段PQ在棱AA1上移动，长为3的线段MN在棱CC1上移动，
点R在棱BB1上移动，则四棱锥R–PQMN的体积是（ ）
A.6 B.10 C.12 D.不确定
8.用1，2，3，4这四个数字可排成必须含有重复数字的四位数有 ( )
A.265个 B.232个 C.128个 D.24个
9.已知定点
，
，动点
在轴正半轴上，若
取得最大值，则点的坐标是 （ ）
A．
B.
C.
D.这样的点不存在
10.设
、
、、
均为正数,且、为常数,、为变量.若
,则
的最大值为 ( )
A. 
B. 
C. 
D.
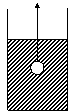11.如图所示，在一个盛 水的圆柱形容器内的水面以下，有一个用
细线吊着的下端开了一个很小的孔的充满水的薄壁小球，当慢
慢地匀速地将小球从水下向水面以上拉动时，圆柱形容器内水
面的高度h与时间t的函数图像大致是（ ） 图3
 |
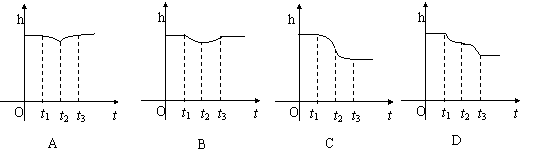图4
12.4个茶杯荷5包茶叶的价格之和小于22元,而6个茶杯和3包茶叶的价格之和大于24,则2个茶杯和3包茶叶的价格比较 ( )
A.2个茶杯贵 B.2包茶叶贵 C.二者相同 D.无法确定
二、填空题(本大题共4小题，每小题4分，共16分。把答案填在题中横线上)
13.对于在区间[,]上有意义的两个函数
和
，如果对任意
，均有
,那么我们称和在[,]上是接近的．若函数
与
在[,] 上是接近的，则该区间可以是 .
14.在等差数列
中,已知前20项之和
,则
.
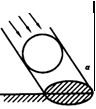15.如图，一广告气球被一束入射角为
的平行光线照射，
其投影是长半轴长为5米的椭圆，则制作这个广告气球
至少需要的面料为 .
图5
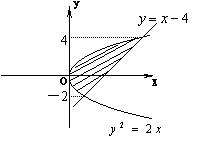
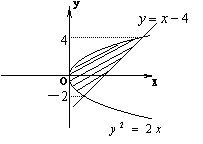
16.由
及
围成几何图形的面积是
.
三、解答题(本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知
.
（Ⅰ）化简f（x）的解析式；
（Ⅱ）若0≤θ≤π，求θ，使函数f（x）为偶函数；
（Ⅲ）在（Ⅱ）成立的条件下，求满足
的x的集合.
18.(本小题满分12分)
甲、乙两人独立解出某一道数学题的概率相同，已知该题被甲或乙解出的概率为0.36，求：（1）甲独立解出该题的概率；
（2）解出该题的人数ξ的数学期望.
19.(本小题满分12分)
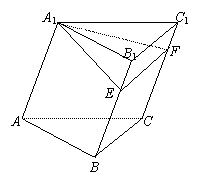如图，已知三棱柱ABC—A1B1C1的棱长都是2，点A1与AB、AC的距离都等于
，且A1E⊥B1B于E，A1F⊥C1C于F.
（1）求证：平面A1EF⊥平面B1BCC1； 图6
（2）求点A到平面B1BCC1的距离；
（3）求平面A1EF与平面A1B1C1所成二面角的大小.
20.(本小题满分12分)
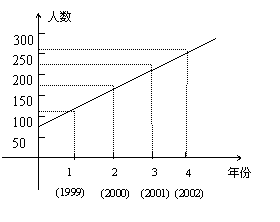
某中学，由于不断深化教育改革，办学质量逐年提高。1999年至2002年高考上线人数如下：
| 年 份 | 1999 | 2000 | 2001 |
|
| 高考上线人数 | 116 | 172 | 220 | 260 |
2002以年份为横坐标，当年高考上线人数为纵坐标建
立直角坐标系，由所给数据描点作图（如图所示），
从图中可清楚地看到这些点基本上分布在一条直
线附近，因此，用一次函数
来模拟高
考上线人数与年份的函数关系，并以此来预测 图7
2003年高考上线人数.如下表：
| 年 份 | 1999 | 2000 | 2001 | 2002 |
| 年份代码 | 1 | 2 | 3 | 4 |
| 实际上线人数 | 116 | 172 | 220 | 260 |
| 模拟上线人数 |
|
|
|
|
为使模拟更逼近原始数据，用下列方法来确定模拟函数。
设
，
、
、
、
表示各年实际上线人数，
、
、
、
表示模拟上线人数，当
最小时，模拟函数最为理想。试根据所给数据，预测2003年高考上线人数。
21.(本小题满分12分)
设集合A＝{1,2,3,…,n} (n∈N)
（Ⅰ）从A中任取两个元素x,y(x≠y)作和式，并且我们将x+y与y+x视为不同和式，试求所有可能出现的和式相加后的总和S；
（Ⅱ）设a1<a2<a3<…<am(m∈M)是集合A中的m个元素，它们组成集合B，且满足每当ai+aj≤n(1≤I≤j≤m)时，就有某个属于B的元素ak(1≤k≤m)使得ai+aj=ak成立，试证：a1+a2+a3+…+am≥
22.(本小题满分14分)
抛物线方程
，直线x+y=t与x轴的交点在抛物线准线的右边.
（1）求证：直线与抛物线总有2个交点；
（2）设直线与抛物线交点为A、B，且OA⊥OB，求P关于t的函数f(t)的表达式；
（3）在（2）的条件下，若t变化，使得原点O到直线AB的距离不大于
，求P的取值范围.
高三数学第二次模拟测试
一、选择题
D B D B C ,B A B C C ,C A
二、填空题：
13. [1,2]∪[3,4]
14. 34 15. 
16. 3
三、解答题：
17.解：（Ⅰ）
…………………………………………2分
……………………………………………………4分
=
…………………………6分
（Ⅱ）当
时，f（x）为偶函数………………………………………………………………8分
（Ⅲ）由
……………………………………………………10分
∴
………………………………………………12分
18.(理)解：(1)设甲、乙独立解出该题的概率为x，则该题不能被甲或乙解出的概率为
（1－x）2，…………………………………………………………2分
由题意可知： 1－（1－x）2=0.36 ………………………………4分
解得：x=0.2 ………………………………………………………6分
(2）解出该题的人数ξ的分布列为：
| ξ | 0 | 1 | 2 |
| P | 0.64 | 0.32 | 0.04 |
……………8分）
Eξ=0×0.64+1×0.32+2×0.04=0.4……………………………11分
答：（略） …………………………………………………………………12分
19. 证明
（1）
.
∴平面A1EF⊥平面B1BCC1.…………………………………………3分
（2）由于A1A//平面B1BCC1，故点A、A1与平面B1BCC1的距离相等.
∵ABB1A1为菱形，故A1E=A1F=.∵B1B⊥平面A1EF，
EF
平面A1EF，∴BB1⊥EF，从而EF=BC=2.
∴△A1EF是等腰直角三角形。取EF中点M，则A1M⊥EF，且A1M=1.
从而A1M⊥平面B1BCC1，即A1M是点A1与平面B1BCC1的距离，
∵点A与平面B1BCC1的距离为1.……………………………………7分
（3）设平面A1EF与平面A1B1C1所成的二面角的棱为直线l，取B1C1的中点N，
则A1N⊥B1C1，但B1C1//EF，∴B1C1//平面A1EF，于是B1C1//l，
在△A1B1C1中，A1N=
∴A1M⊥l，A1N⊥l，
即∠MA1N为所求二面角的平面角.……………………………………10分
∵A1M⊥平面B1BCC1，∴A1M⊥MN. ∴cos∠NA1M=
，
故所求二面角的大小为
……………………………………12分.
20解：
…………4分
当
即
① 时 ，S有最小值，其中最小值为：M=
………………………………………………………8分
当且仅当
时，M有最小值。∴代入①得
。
∴
。
故2003年高考上线人数为312人 …………………………………………12分
21. 解：（Ⅰ）从A中任取两个元素作和式，当x+y与y+x为不同的和式时，共有
个和式，
………………………………………………2分
又每个元素在这个和式中出现的次数相同，且为2
＝2(n-1)次……4分
故S=2(n-1)(1+2+3+…+n)=n(n2-1)……………………………………………6分
（Ⅱ）证明：显然，a1+am≥n+1
否则a1+am≤n，依题意设存在一个ak(1≤k≤m)使ak=a1+am，
又∵a1+am>am,∴ak>am，且ak∈B，这与ak为B中最大的元素相矛盾，
即a1+am≥n+1……………………………………………………………9分
用反证法可证：a2+am-1≥n+1
假设a2+am-1≤n，依题意设存在一个ak(1≤k≤m)使ak=a2+am-1
又∵a1+am-1<a2+am-1≤n
∴另存在一个
(1≤k1≤m)，使=a1+am-1
即存在两个不同的数ak、∈B，且>am-1,ak>am-1
这与题设在B中只有一个数大于am-1相矛盾，
故a2+am-1≥n+1
同理可证：对任意的i(1≤i≤m)，有ai+am+1-i≥n+1，
故a1+a2+a3+…+am=
[(a1+am)+(a2+am-1)+…+(am+a1)]≥……12分
22. 证明：
(1)抛物线的准线
……………………………………………………1分)
由直线x+y=t与x轴的交点(t，0)在准线的右边得：
即4t+p+4＞0 ……………………………………………………2分
由
①
∵p＞0 4t+p+4＞0 ∴△=（2t+p）2－4（t2－p）=p（4t+p+4）＞0 ……4分
故直线与抛物线总有2个交点 …………………………………………………5分
(2)解：设A（x1，y1），B（x2，y2），则x1，x2是方程①的2个根，由根与系数关系
得：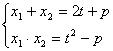
………………………………………………………7分
∵OA⊥OB ∴KOA·KOB=－1 即x1x2+y1y2=0 ………………………………8分
又∵A、B在直线x+y=t上 ∴y1=t－x1 y2=t－x2
∴x1x2+y1y2=t2－（t+2）p=0
由P＞0，及4t+p+4＞0 ……………………………9分
得：f(t)的定义域为（－2，0）∪（0，+∞） ………………………………10分
(3)解：由已知得：
由②知x＞－2且t≠0
………………………………………………………………11分
又
（12分）令u=t+2
∴
则
在[1、2
上是减函数，在（2，3
上是增函数
从而
或
∴当
当
……………………………13分
综上所述，P的取值范围是
……………………………………………14分
| |||||
 | |||||
 | |||||
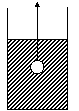图1 图2 图3
 |
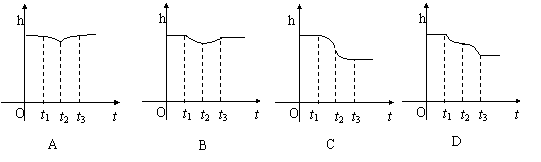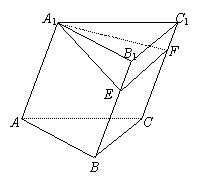图4
|
图5 图6
 |
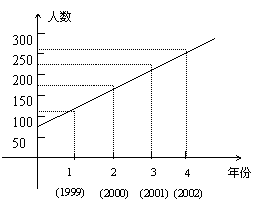图7