高三年级统考试题数学参考答案及评分标准(文史类)
说明：
1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．
2．对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．
3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
4．只给整数分数，选择题和填空题不给中间分数．
一．选择题：AAABB CBABD DC
二．填空题：13．1 14．19 15．400 16．
三．解答题：
17．解：解：a · b
2分
a＋b 
4分
∴cos x≥0，因此 a＋b ＝2 cos x
6分
∴0≤cos x≤1
∴当且仅当
取得最小值
． 12分
18．(1)解：取3个球的方法数为
2分
设“3个球全红色”为事件A，“3个全蓝色”为事件B，“3个球全黄色”为事件C，则
，
，
4分
∵A、B、C为互斥事件
∴P(A＋B＋C)= P(A)＋P(B)＋P(C)
8分
(2)解：记“3个球中至少有一个是红球”为事件D，则
为“3个球中没有红球”
12分
19．(1)解：设{xn}的公比为q(q≠1)
∵
∴{yn}为等差数列，设公差为d 2分
∵y3＝18，y6＝12，∴d＝－2
∴yn＝y3＋(n－3)(－2)＝24－2n 4分
设前k项和为最大，则
∴前11项和与前12项和为最大，且最大值为132 6分
(2)解：由(1)得：2logaxn＝24－2n ，∴xn＝a12－n，n∈N* 8分
若xn＞1，则a12－n＞1
当a＞1时，n＜12，显然不存在满足条件自然数M 10分
当0＜a＜1时，n＞12，
∴存在M＝12，13，14，…，使当n＞M时，xn＞1恒成立，且M的最小值为12 12分
|
|
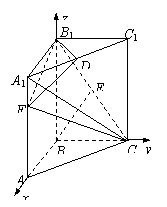
20．方法一：
(1)解：以
为x轴、y轴、z轴建立空间直角坐标系
∵AC＝2a，∠ABC＝90°
∴AB＝BC＝
从而A (，0，0)，C (0，，0)，A1(，0，3a)，B1(0，0，3a)，C1(0，，3a) 2分
∴D(
)，E(
)
∴
，
4分
因此
∴
6分
(2)证：F(，0，2a)，
，
，
8分
∵
10分
∴CF⊥B1D，CF⊥B1F
∴CF⊥平面B1DF． 12分
方法二：
(1)解：取A1B1中点G，连EG，则EG∥A1C，连BG
则GE与BE所成的角即为异面直线A1C和BE所成的角
2分
在△BEG中，GE
，
4分
∴
∴
6分
(2)证：∵D是A1C1中点，∴B1D⊥A1C1 ，故B1D⊥平面A1ACC1
因此B1D⊥CF
8分
在Rt△B1FC中，
，
在Rt△AFC中，
在 Rt△BB1C中，
10分
∵B1F2+FC2=B1C2，∴CF⊥FB1
∴CF⊥平面B1DF 12分
21．(1)解：由
得： (1＋a)x2＋2ax＋(a－1)＝0 ①
若1＋a＝0，则直线l与双曲线C的渐近线平行，故l与C只可能有一个交点，不合题意
∴1＋a≠0 2分
设P(x1，y1)，Q(x2，y2)，则
，且△＝4a2－4(a－1)(a＋1) ＝4＞0
4分
若
，则
，解得：a＝或a＝3
∴当a＝或a＝3 时， 6分
(2)解：
若存在实数a，使
，则
Û x1x2＋y1y2＝0 8分
即x1x2＋(x1＋1)(x2＋1)＝0 Û 2x1x2＋(x1＋x2)＋1＝0
∴
＝0，解得：a＝1
∴存在实数a＝1，使得 12分
22．(1)解：
，∴曲线y＝f (x)在点M (x1，f (x1))处的切线的斜率
∴切线l的方程为
，即
4分
(2)解：令y＝0得
①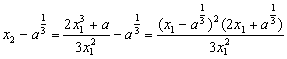
≥0 (*) 8分
∴
，当且仅当
时等号成立． 10分
②∵
，∴(*)中“＝”不成立，故
12分
∵
∴
，故x2＜x1
∴当时，
成立． 14分