高三数学归纳法及应用举例复习指导

高三数学归纳法及应用举例复习指导

重点难点分析：
　　（1）数学归纳法的第一步是验证命题递推的基础，第二步是论证命题递推的依据，两个步骤密切相关，缺一不可。
　　（2）归纳思想充分体现了辩证唯物主义的特殊与一般的思想，是数学的基本思想，数学归纳法体现了有限与无限的辩证关系与转化思想。
　　（3）归纳——猜想——证明是经常运用的数学方法，观察是解决问题的前提条件，需要进行合理的试验和归纳，提出合理的猜想，从而达到解决问题的目的。
　　（4）数学归纳法的应用通常与数学的其它方法联系在一起，如比较法，放缩法，配凑法，分析法和综合法等。
　　典型例题：
　　例1．用数学归纳证明：=
-n(n+1)(4n+3)。
　　证明：①当n=1时，左边，右边=-1(1+1)(4+3)=-14，等式成立。
　　②假设n=k时等式成立，
　　即=-k(k+1)(4k+3)。
　　那么n=k+1时，
　　　+[(2k+1)(2k+2)²-(2k+2)(2k+3)²]
　　=-k(k+1)(4k+3)-2(k+1)(4k²+12k+9-4k²-6k-2) =-(k+1)[4k²+3k+2(6k+7)]=-(k+1)(4k²+15k+14)
　　=-(k+1)(k+2)(4k+7)=-(k+1)[(k+1)+1][4(k+1)+3]，等式也成立。
　　由①②知，当n∈N′时等式成立，∴原命题成立。
　　例2．试证S_n=n³+(n+1)³+(n+2)³能被9整除。
　　证明：①n=1时，S₁=4×9，能9整除。
　　②假设，n=k时，S_k能被9整除，则S_k+1=(k+1)³+(k+2)³+(k+3)³=S_k+(k+3)³-k³=S_k+9(k³+3k+3)
　　由归纳假设知S_k+1能被9整除，也就是说n=k+1时命题也成立。
　　综上所述：命题成立。
　　点评：用数学归纳法证明整除问题时，关键是把n=k+1时的式子分成两部分，其中一部分应用归纳假设，另一部分经过变形处理，确定其能被某数（某式）整除。
　　例3．通过一点有n个平面，其中没有任何3个平面交于同一条直线，用数学归纳法证明这些平面把空间分成(n²-n+2)个部分。
　　证明：设适合条件的n个平面把空间分成p_n个部分，∴p_n=n²-n+2
　　①当n=1时，p₁=1-1+2=2，显然符合条件，故命题成立。
　　②假设当n=k时，命题成立，即满足命题条件的k个平面把空间分成p_k=k²-k+2个部分，
　　那么当n=k+1时，即如果再有一个平面a适合条件，那么，在平面α上必有k条交线，
　　∴平面α被分成2k个部分，∴p_k+1=p_k+2k=k²-k+2+2k=(k+1)²-(k+1)+2。
　　∴当n=k+1时，p_n=n²-n+2成立。
　　综上①②可知对任何n∈N′，命题成立。
　　点评：几何计数问题应抓住所划分的线段、平面、空间的个数与交点、交线间的关系等。
　　例4．若不等式对一切正自然数n都成立，求自然数a的最大值，并证明你的结论。
　　证明：n=1时，，即，所以a<26，而a∈N，所以取a=25，
　　下面用数学归纳法证明：。
　　(1) n=1时，已证。
　　(2) 假设当n=k时，有：，
　　则当n=k+1时，有
　　
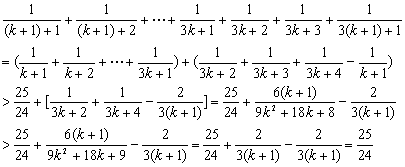
　　所以①②知对一切n∈N′ 都有：。
　　例5．在数列{a_n}中，已知a₁=-lga, a_n-1=a_n-lga^n-1 (n≥2)，先求出a₂,a₃,a₄，观察所得结果，推测{a_n}的通　　　　　 项公式，并用数学归纳法证明。
　　解析：因为a_n-1=a_n-lga^n-1 (n≥2)，所以a_n=a_n-1+(n-1)lga (n≥2)，
　　又a₁=-lga, 所以a₂=a₁+(2-1)lga=-lga+(2-1)lga=(-1+2-1)lga, a₃=a₂+(3-1)lga=(-1+2-1+3-1)lga,
　　a₄=a₃+(4-1)lga=(-1+2-1+3-1+4-1)lga。
　　由此推判。
　　下面用数学归纳法证明。
　　（1）n=1时，，猜想正确。
　　（2）假设n=k时，猜想正确，即，
　　则，
　　即n=k+1时，猜想也正确。
　　由（1）（2）知，对于任意n∈N′，都有。
　　训练题：
　　1．用数学归纳法证明凸n边形的对角线条数（n≥4,n∈N）时，f_(k+1)与f_(k)的关系是______。
　　2．k为正偶数，p_(k)表示等式，则p₍₂₎表示等式______。p₍₄₎表示等式______。由p_(k)p_(k+2)时，可在p_(k)两边同时加上____。
　　3．用数学归纳法证明 3⁴ⁿ⁺²+5²ⁿ⁺¹ (n∈N′)能被14整除。
　　4．用数学归纳法证明(n+1)(n+2)……(n+n)=2ⁿ·1·3·5……(2n-1) (n∈N′)
　  5．已知。 　（1）计算及的值。
　　（2）归纳出 (n∈N′)的值，再用数学归纳法加以证明。
　　参考答案： 　　1．f_(k+1)=f_(k)+k-1
　　2．
　3. ①n=1时，3⁶+5³=61×14能被14整除。
　　②假设n=k时命题成立，那么n=k+1时，也能被14整除（以下略）。
　　4．①当n=1时，等式左边=2，等式右边=2，∴等式成立。
　　②假设n=k(k∈N′)等式成立，即(k+1)(k+2)……(k+k)=2^k·1·3·5……(2k-1)成立，
　　那么n=k+1时，(k+2)(k+3)……(k+k)(2k+1)(2k+2)=2(k+1)(k+2)(k+3)……(k+k)(2k+1)
　　　　　　　　=2^k+1·1·3·5……(2k-1)[2(k+1)-1]
　　即n=k+1时等式成立。（以下略）。
　　5．(1) ，。　(2) 猜想 (n∈N′)
　　证明：①n=1，2时，已证。
　　②假设n=k及n=k-1 (k≥2)，命题成立，
　　即，，
　　则n=k+1时，
　　　　　　　（以下略）。
　　（注意这种证明方法与前面的方法不同）