高三数学教学测试（一）
一、选择题
1．函数y=12sin (2x - ) – 5sin(2x + )的最大值是 （ ）
A．5 B．12 C．13 D．15
2. 已知函数y=logax的图象与其反函数的图象有交点，且交点的横坐标为 x0，则有 （ ）
A．a>1且x0>1 B．0<a<1且0<x0<1 C．a>1且0<x0<1 D．0<a<1且x0>1
3．两个完全相同的长方体的长、宽、高分别为5cm，4cm，3cm，把它们重叠在一起组成一
个新长方体，在这些新长方体中，最长的对角线的长度是
（ ） A．
B．
C．
D．
4．期中考试以后，班长算出了全班40个人数学成绩的平均分为M. 如果把M当成一个同学的分数，与原来的40个分数一起，算出这个41个分数的平均值为N，那么M:N为 （ ）
A．
B．1 C．
D．2
5．将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次，使点（2，0）与点（－2， 4）重合，若点（5，8）与点（m ,n）重合，则m+n的值为 （ ）
A．4 B．－4 C．13 D．－13翰林汇
6．设函数
若f(x0)>1，则x0的取值范围是
（ ）
A．（0，10） B．（—1，+∞）
C．（—∞，—2）∪（—1，0） D．（—∞，0）∪（10，+∞）
7．设A、B两点的坐标分别为(-1,0),(1,0)，条件甲：
； 条件乙：点C的坐标是方程 + = 1 (y¹0)的解. 则甲是乙的
（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不是充分条件也不是必要条件
8．长为2的线段PO⊥平面α，O为垂足，A、B是平面α内两动点，若tan∠PAO= 
，
tan∠PBO=2,则P点到直线AB的距离的最大值是
（ ） A．2
cm B．
cm C．cm D．
cm
9．设动点P在直线
上，O为坐标原点．以OP为直角边，点O为直角顶点作等腰
，则动点Q的轨迹是 （ ）
A．圆 B．两条平行直线 C．抛物线 D．双曲线
10．已知△ABC中，点D在BC边上，且
则
的值是（ ）
A．
B．
C．－3 D．0
11．三个数
成等比数列，若有
成立，则
的取值范围是
（ ）
A．
B．
C．
D．
12．点P在曲线y=x3－x+7上移动，过P点的切线的倾斜角取值范围是 （ ）
A．
B．
C．
D．
二、填空题
13．若z=
满足约束条件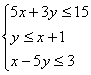
，则Z的最大值和最小值分别为
．
14．
的展开式中，奇次项系数和为
.
15．一次测量中出现正误差和负误差的概率都是，在5次测量中恰好出现2次正误差的概率是
．
16．已知
是两条直线，
是两个平面，有下列4个命题：
①若
，则
②若
，则
③若
则
④若异面， 
,则
.
其中正确命题有 ．
三、解答题
17．已知实数
，函数
有极大值32.
（Ⅰ）求实数
的值；
（Ⅱ）求函数
的单调区间.
18．已知向量
，定义函数
，求函数
的最小正周期、单调递增区间．
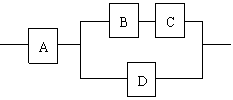19．如图：用A、B、C、D四类不同的元件连接成系统N，当元件A正常工作且元件B、C都正常工作，或当元件A正常工作且元件D正常工作时，系统N正常工作.已知元件A、B、C、D正常工作的概率依次为
（Ⅰ）求元件A不正常工作的概率；
（Ⅱ）求元件A、B、C都正常工作的概率；
（Ⅲ）求系统N正常工作的概率.
20．如图矩形ABCD中，AB=2BC，E为CD的中点．将矩形沿AE折成二面角D1—AE—B，使BD1=CD1．
|
（Ⅱ）求异面直线AE与CD1所成的角．
21．已知数列{an}（n∈N*）满足3a5=8 a12>0，且三点P(n-2，an)、Q(n，an+1)、R(n+2，an+2)在一条直线上.
（Ⅰ）若a1=76，求通项公式an；
（Ⅱ）若bn=anan+1an+2（n∈N*），则数列{bn}的项中是否均为正数？如果是，则说明理由；如果是，则数列{bn}的项中有多少为正数？
（Ⅲ）若数列{bn}的前n项的和为Sn，当n取多大值时，Sn取得最大值？并证明你的结论.
22．已知A﹑B﹑D三点不在一条直线上，且A（-2，0），B（2，0）， 
=2，
= (
+).（1）求E点的轨迹方程；
（2）过A作直线交以A、B为焦点的椭圆于M、N两点，线段MN的中点到y轴的距离为 ，且直线MN与E点的轨迹相切，求椭圆的方程.
高三数学教学测试（一）参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | C | B | C | D | B | C | B | D | D | D |
二、填空题
13．17和－11
14．4 15．
16．②③
三、解答题
17．解（Ⅰ）
令
，得
或2. ……2′∵函数有极大值32，
在时取得极大值.
解得
当
时，
当
时，
在时，有极大值32.
时函数有极大值32.
（Ⅱ）由
得或
∴函数的单调增区间是（－
；单调减区间是（
18．解：因为
，所以
故
令
，则
的单调递增的正值区间是
，单调递减的正值区间是
所以（1）当
时，函数的单调递增区间为；
（2）当
时，函数的单调递增区间为 ．
19．解：（Ⅰ）元件A正常工作的概 率P（A）=，它不正常工作的概率
=
（Ⅱ）元件A、B、C都正常工作的概率P(A·B·C)=P（A）P（B）P（C）
（Ⅲ）系统N正常工作可分为A、B、C都正常工作和A、D正常工作但B、C不都正常工作两种情况，前者概率
，后者的概率为
．
所以系统N正常工作的概率是
．
20．（Ⅰ）证明：取AE中点F，BC中点G，连结D1F，FG，D1G.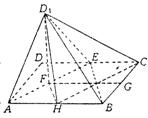 
由题意知，AD1=D1E，BD1=CD1，
∴D1F⊥AE，D1G⊥BC. FG⊥BC,∴BC⊥平面D1FG , ∴BC⊥D1F， 又D1F⊥AE，AE与BC相交，∴D1F⊥平面ABC，∴平面AD1E⊥平面ABC.
（Ⅱ）解：取AB中点H，连结CH，则CH//AE，∴ ∠D1CH即为AE与CD1所成的角.
连结D1H，CF，HF. ∵D1F⊥平面ABC,D1F⊥CF, D1F⊥FH. 设AB=
，∴△CEF中，
在Rt△D1CF中，
在Rt△D1FH中，
在△D1CH中，
∴所求角的大小是
.
21．解：(Ⅰ)由题意有 = ，即an+1- an = an+2- an+1 .
∴数列{an}为等差数列. 设公差为d，又3a5=8 a12，∴3(a1+4d)=8(a1+11d)，即5 a1+76d=0.
而a1=76，∴d= -5.
故an=76-5(n-1)=81-5n.
(Ⅱ)由(Ⅰ)可知a1= - d，∴a5= - d > 0，∴d < 0.
∴数列{an}是首项为正数的递减的等差数列.
由an= a1+(n-1)d= - d+(n-1)d≥0，解得n≤16，即n≤16.
∴数列{bn}的项中前16项为正数.
(Ⅲ)∴a1> a2> a3> …> a16> 0 > a17> a18> …，∴b1> b2> b3> …> b14> 0 > b17> b18> ….
而b15= a15 a16 a17<0，b16= a16 a17 a18>0.
∴ S1< S2< S3< … < S14，S14> S15，S15< S16，S16> S17 > S18>….
又a15= - d > 0，a18= d < 0.
∴S16- S14= b15+ b16= a15 a16 a17+ a16 a17 a18= a16 a17(a15+ a18) = a16 a17•d>0，，∴S16> S14，
故n=16时，Sn取得最大值．
22．（Ⅰ）设E(x，y)，
= +，则四边形ABCD为平行四边形，而= (+)，
∴E为AC的中点，∴OE为ΔABD的中位线，∴
= =1，∴E点的轨迹方程是
x2+y2=1.
（Ⅱ）设M(x1，y1)，N(x2，y2)，中点为 (x0，y0)，椭圆的方程为 + = 1，直线MN的方程为
y=k(x+2)，由于直线MN与圆x2+y2=1相切，∴ =1，解得k = ±.
∴直线MN的方程为y=k(x+2).
将y=±(x+2)代入方程 + = 1，得 + = 1，即3(a2-4)x2+a2 (x+2)2=3a2(a2-4)，
即4(a2-3)x2+4a2 x+16a2-3a 4=0，∴x0= - = - .
又MN的中点到y轴的距离为 ，∴x0= - ，即 - = - ，解得a=2.
故所求的椭圆的方程为 + = 1.