高三数学教学质量抽测
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页．共150分．考试时间120分钟．
第 I 卷 （选择题 共60分）
注意事项：
1．答第I卷前，考生务必将自己的姓名、考生号、考试科目用铅笔涂写在答题卡上．
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．
3．考试结束，监考人员将本试卷和答题卡一并收回．
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P（A+B）＝P（A）+P（B） S＝4πR2
如果事件A、B相互独立，那么 其中R表示球的半径
P（A·B）＝P（A）·P（B） 球的体积公式
如果事件A在一次试验中发生的概率是P. 
那么n次独立重复试验中恰好发生k次的概 其中R表示球的半径
率
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
（1） 不等式
的解集是
（A） 
（B） 
（C） 
（D） 
（2） 若
是第二象限的角，且
，则
（A） 
（B） 
（C） 
（D） 
（3） 圆的一条直径的端点是A（2，0），B（2，－2），则圆的方程是
（A）
（B）
（C）
（D）
（4） 三棱锥D—ABC的三个侧面分别与底面全等，且AB＝AC＝
，BC＝2，则以BC为棱，以面BCD与BCA为面的二面角的大小为
（A） 300 （B） 450 （C）600 （D）900
（5） 下列各式中，对任何实数
都成立的一个是
（A） 
（B） 
（C） 
（D） 
（6） 等差数列
中，
，那么
的值是
（A） 12 （B） 24 （C） 16 （D） 48
（7） 下列命题中，正确的是
（A）平行于同一平面的两条直线平行
（B）与同一平面成等角的两条直线平行
（C）与同一半平面成相等二面角的两个半平面平行
（D）若平行平面与同一平面相交，则交线平行
（8） 二项式
的展开式的常数项是
（A）20 （B）
（C）540 （D）
（9） 电灯泡使用时数在1000小时以上的概率为0.8，则3个灯泡在使用1000小时内恰好坏了一个的概率为
（A） 0.384
（B） （C） 0.128
（D） 0.104
（10） 已知目标函数z＝2x＋y，且变量x、y满足下列条件：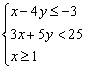
，则
（A） z最大值＝12，z无最小值 （B） z最小值＝3，z无最大值
（C） z最大值＝12，z最小值＝3 （D） z最小值＝
，z无最大值
（11） 探索以下规律：
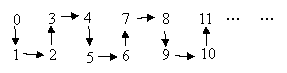
则根据规律，
从2002到2004，箭头的方向依次是
（A） （B） （C） （D）
（12） 已知点M（－3，0），N（3，0），B（1，0），圆C与直线MN切于点B，过M、N与
圆C相切的两直线相交于点P，则P点的轨迹方程为
（A）
（B）
（C）
（x > 0） （D）
高三教学质量抽测
数学
第 Ⅱ 卷 （非选择题 共90分）
注意事项：
⒈ 第Ⅱ卷共4页，用钢笔或圆珠笔直接答在试题卷中．
⒉ 答卷前将密封线内的项目填写清楚．
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分数 | ||||||||
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上。
（13）由数字0、1、2、3、4组成无重复数字的5位数，其中奇数有 个．
（14）一个正四棱锥的底面边长为2，侧棱长为，五个顶点都在同一个球面上，则此球的表面积为
.
（15）曲线
上与直线2x－y－4＝0平行的切线的纵截距是 ．
（16）设函数
,给出以下四个论断：
①
的周期为π； ②在区间（
,0）上是增函数；
③的图象关于点（
,0）对称； ④的图象关于直线
对称.
以其中两个论断作为条件，另两个论断作为结论，写出你认为正确的一个命题：
（只需将命题的序号填在横线上）．
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
（17）（本小题12分）
已知 
＝1，
＝
，
（I）若//，求
；
（II）若，的夹角为135°，求 ＋ ．
（18）（本小题12分）
袋中装有3个白球和4个黑球，现从袋中任取3个球，设ξ为所取出的3个球中白球的个数．
（I）求ξ的概率分布；
（II）求Eξ．
（19）（本小题12分）
如图，已知正方体ABCD－A1B1C1D1的棱长为2，M、N分别为AA1、BB1的中点，求：
（I）CM与D1N所成角的余弦值；
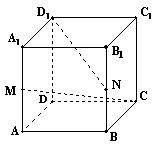（II）异面直线CM与D1N的距离．
（20）（本小题12分）
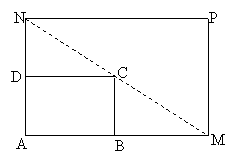
如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN，要求B在AM 上，D在AN上，且对角线MN过C点，AB＝3米，AD＝2米，
（I）要使矩形AMPN的面积大于32平方米，则AN的长应在什么范围内？
（II）若AN的长度不少于6米，则当AM、AN的长度是多少时，矩形AMPN的面积最小？并求出最小面积．
（21）（本小题12分）
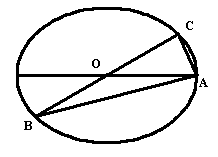
如图所示，已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个端点，BC过椭圆中心O，且
，BC＝2AC．
（I）建立适当的坐标系，求椭圆方程；
（II）如果椭圆上有两点P、Q，使∠PCQ的平分线垂直于AO，证明：存在实数λ，使
．
（22）（本小题14分）
已知数列{a
n}是首项为3，公比为
的等比数列，Sn是其前n项和．
（Ⅰ）试用Sn表示Sn＋1；
（Ⅱ）是否存在自然数c、k，使得
＞3成立？证明你的论断.
高三教学质量抽测数学
参考答案及评分标准
一、CDADA BDDAB CB
二、（13） 36 （14）9π （15） 
（16）①④
②③ 或 ①③②④
三、（17） 解：（I）∵//，
①若，共向，则 ＝•＝ ………………… 3′
②若，异向，则 ＝－•＝－ ……………… 6′
（II）∵，的夹角为135°， ∴ ＝••cos135°＝－1 …… 8′
∴＋2＝（＋）2 ＝2＋2＋2＝1＋2－2＝1 ………… 11′
∴
……………………………………12′
（18）解：（I）ξ的可能取值为0，1，2，3. …………………………………… 1′
∵P（ξ＝0）＝
＝
； P（ξ＝1）＝
＝
；
P（ξ＝2）＝
＝
； P（ξ＝3）＝
＝
. ………… 5′
∴ξ的分布列为：
| ξ | 0 | 1 | 2 |
| ||
|
P |
|
|
|
|
（II）Eξ＝0×＋1×＋2×＋3×＝
. ………………………………… 12′
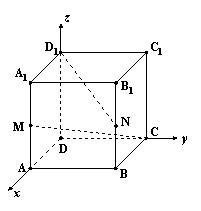（19）解：（I）如图，以D为原点，DA、DC、DD1分别为x、y、z轴，建立空间直角坐标系，……………1′
则C（0，2，0）、D1（0，0，2）、M（2，0，1）、N （2，2，1），
∴
＝（2，－2，1），
＝（2， 2，－1），……3′
设CM与D1N所成的角为α，
则cosα＝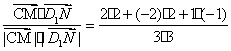
＝－
＜0
∴α为钝角，∴CM与D1N所成的角为θ＝π－α，即cosθ＝
（解法2：设CM与D1N所成的角为θ，
则cosθ＝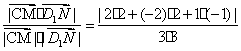
＝）………………………………6′
（II）取DD1的中点E，分别连接EM、EB，则EM∥BC，EB∥D1N，
∴B、C、E、M共面且D1N∥平面BCEM，
∴D1到平面BCEM的距离d等于异面直线CM与D1N的距离， ……………………8、
∵
＝（―
―
）·23＝
…………10、
即
SBCEM·d＝
而SBCEM＝BM·BC＝2
∴d＝
………………………………………………………………………………12、
解法2： 设，
的法向量为
＝（x，y，z）
则
，
取＝（0，1，2）………………………………8′
∴异面直线CM与D1N的距离d＝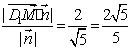
………12′
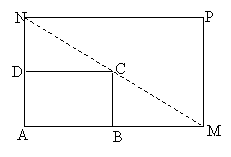（20）解：设AN的长为x米（x >2）
∵
，∴AM＝
∴SAMPN＝AN•AM＝
……… 3′
（I）由SAMPN
> 32 得 > 32 ，
∵x >2，∴
，即（3x－8）（x－8）> 0
∴
即AN长的取值范围是
……… 6′
（II） 令y＝，则y′＝
……… 8′
∴当x > 4，y′> 0，即函数y＝在
上单调递增，
∴函数y＝在
上也单调递增。
……… 10′
∴当x＝6时y＝取得最小值即SAMPN取得最小值27（平方米）
此时AN＝6米，AM＝4.5米 ……………… 12′
（21）解：（I）以O为原点，OA为X轴建立直角坐标系，设A（2，0），则椭圆方程为
……………………………………………… 2′
∵O为椭圆中心，∴由对称性知OC＝OB
又∵
， ∴AC⊥BC
又∵BC＝2AC ∴OC＝AC
∴△AOC为等腰直角三角形
∴点C的坐标为（1，1） ∴点B的坐标为（－1，－1）…………………… 4′
将C的坐标（1，1）代入椭圆方程得
，
则求得椭圆方程为
…………………………………… 6′
（II）由于∠PCQ的平分线垂直于OA（即垂直于x轴），不妨设PC的斜率为k，则QC的斜率为－k，因此PC、QC的直线方程分别为y＝k（x－1）+1，y＝－k（x－1）+1
由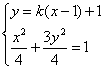
得（1＋3k2）x2－6k（k－1）x＋3k2－6k－1＝0 （*）…… 8′
∵点C（1，1）在椭圆上，
∴x＝1是方程（*）的一个根，∴xP•1＝
即xP＝
同理xQ＝
……………………………………………………… 9′
∴直线PQ的斜率为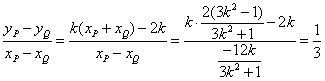
（定值）
…………………………………………………………………………11′
又∠ACB的平分线也垂直于OA
∴直线PQ与AB的斜率相等（∵kAB=）
∴向量
，即总存在实数
，使
成立．………………… 12′
（22）解：（I）∵a1＝3，q＝，
∴Sn＝6(1－
)， Sn＋1＝6(1－
)
…………………………………………… 2′
∴
Sn＋1＝ Sn＋3
………………………………………… 4′
（II）∵＞3
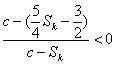…………（*） …………………………………6′
而Sk＝6(1－
)＜6，∴Sk－（
Sk－
）＞0
即 Sk＞（ Sk－） ……………………………………………………………… 7′
由（*）得 （ Sk－）＜c＜Sk …………① …………………………………8′
∵ Sk＋1＞Sk，故 Sk－≥ S1－＝
…………………………………………… 9′
又Sk＜6，∴＜c＜6
故要使①成立，c只能取3、4或5 ………………………………………………… 10′
当c＝3时，由①式得2＜2k＜
，显然k不存在 …………………………………… 11′
当c＝4时，由①式得3＜2k＜
，显然k也不存在…………………………………… 12′
当c＝5时，由①式得6＜2k＜
，显然k也不存在…………………………………… 13′
综上所述，不存在自然数c、k，使得＞3 成立…………………………… 14′