高三数学教学质量检测试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题（本大题共12小题，每小题5分，共60分.在每小题的四个选项中，只有一项是符合题目要求的）
1.设集合M={x－1≤x＜2},N={xx≤a}.若M∩N≠
,则a的取值范围是
A.（－∞,2］ B.(－1,+∞) C.［－1,+∞) D.［－1,1］
2.若椭圆
过点（－2，
），则其焦距为
A.2
B.2
C.4
D.4
3.已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则
=－1是l1⊥l2的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分，也不必要条件
4.已知函数f1(x)=sin(
－x),f2(x)=sinxcosx,f3(x)=－arccosx,f4(x)=tgx,从中任取两个相乘得若干个函数，其中偶函数的个数为
A.2 B.3 C.4 D.6
5.在5张卡片上分别写着数字1、2、3、4、5，然后把它们混合，再任意排成一行，则得到的数能被5或2整除的概率是
A.0.8 B.0.6 C.0.4 D.0.2
6.若loga(a2+1)＜loga2a＜0,则a的取值范围是
A.0＜a＜1
B.0＜a＜
C.＜a＜1
D.a＞0且a≠1
7.已知f(x)=ax3+3x2+2,若f′(－1)=4,则a的值等于
A.
B. 
C.
D.
8.把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半，纵坐标扩大到原来的两倍，然后把图象向左平移
个单位，则所得图形表示的函数的解析式为
A.y=2sin2x B.y=－2sin2x
C.y=2cos(x+)
D.y=2cos(
)
9.对函数f(x)=ax2+bx+c(a≠0),作x=h(t)的代换，总不改变函数f(x)的值域的代换是
A.h(t)=10t B.h(t)=t2 C.h(t)=sint D.h(t)=log2t
10.如图正方体ABCD—A1B1C1D1中，E、F分别是正方形ADD1A1和ABCD的中心，G是CC1的中点，设GF、C1E与AB所成的角分别为α、β,则α+β等于
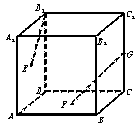A.120°
B.90°
C.75° D.60°
11.若集合A1、A2满足A1∪A2=A，则称（A1，A2）为集合A的一个分拆，并规定：当且仅当A1=A2时，（A1，A2）与（A2，A1）为集合A的同一种分拆，则集合A={a1,a2,a3}的不同分拆种数是
A.27 B.26 C.9 D.8
12.二次函数f(x)的二次项系数为正，且对任意实数x，恒有f(2+x)=f(2－x),若f(1－2x2)＜f(1+2x－x2)，则x的取值范围是
A.x＞2 B.x＜－2或0＜x＜2
C.－2＜x＜0 D.无法确定
第Ⅱ卷(非选择题 共90分)
二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）
13.若双曲线离心率为2，则它的两条渐近线的夹角等于_______.
14.已知函数y=f(x)的反函数f－1(x)=logsin
(x－cos2
),则方程f(x)=1的解是_______.
15.对于实数x,y,定义新运算x﹡y=ax+by+1,其中a、b是常数，等式右边是通常的加法和乘法运算，若3﹡5=15，4﹡7=28，则﹡=_____.
16.设α、β表示平面，l表示不在α内也不在β内的直线，存在下列三个事实①l⊥α,②l∥β,③α⊥β，若以其中两个作为条件，另一个作为结论，可构成三个命题，其中真命题是________.（要求写出所有真命题）
三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）
17.（本小题满分12分）
复数w满足i－w=1,arg(1－w)=
（Ⅰ）求w的值.
（Ⅱ）设z=cosθ+isinθ,求λ=z－w的最大值.
18.（本小题满分12分）
数列{an}中，a1=1,n≥2时，其前n项的和Sn满足Sn2=an(Sn－)
（Ⅰ）求Sn的表达式.
（Ⅱ）设bn=
,数列{bn}的前n项和为Tn，求
.
19.（本小题满分12分）
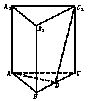
如图正三棱柱，棱都相等，D是BC上一点，AD⊥C1D.
（Ⅰ）求证：截面ADC1⊥侧面BCC1B1.
（Ⅱ）求二面角C—AC1—D的大小.
（Ⅲ）若AB=2，求A1B与截面ADC1的距离.
20.（本小题满分12分）
在中国轻纺市场，当季节即将来临时，季节性服装价格呈上升趋势，设某服装开始时定价为10元，并且每周（七天）涨价2元，5周后保持20元的价格平稳销售，10周后当季节即将过去时，平均每周销价2元，直到16周末，该服装已不再销售.
（Ⅰ）试建立价格p与周次t的函数关系.
（Ⅱ）若此服装每件进价Q与周次t之间的关系Q=－0.125（t－8）2+12,t∈［0,16］,
t∈
.试问该服装第几周每件销售利润L最大？
21.（本小题满分12分）
函数f(x)=loga(x－3a)(a＞0,且a≠1),当点P（x,y)是函数y=f(x)图象上的点时，Q（x－2a,－y)是函数y=g(x)图象上的点.
（Ⅰ）写出函数y=g(x)的解析式.
（Ⅱ）当x∈［a+2,a+3］时，恒有f(x)－g(x)≤1,试确定a的取值范围.
22.（本小题满分14分）
椭圆E中心在原点O，焦点在x轴上，其离心率
,过点C（－1，0）的直线l与椭圆E相交于A、B两点，且C分有向线段
的比为2.
（Ⅰ）用直线l的斜率k(k≠0)表示△OAB的面积;
（Ⅱ）当△OAB的面积最大时，求椭圆E的方程.
高三数学教学质量检测试题
一、1.C 2.D 3.A 4.B 5.B 6.C 7.C 8.B 9.D 10.B 11.A 12.C
二、13. 60° 14.x=2 15.－11
16.①②
③,①③②
17.解：（Ⅰ）设1－w=－bi(b＞0) 1分
∴w=1+bi，∴i－1－bi=1
即1+(1－b)2=1
∴b=1，∴w=1+i 6分
（Ⅱ）λ=z－w=cosθ+isinθ－1－i=
≤
10分
∴λmax=
+1
18.（Ⅰ）n≥2 Sn2=(Sn－Sn－1)(Sn－) 2分
∴
即
（n≥2） 4分
∴
∴
6分
（Ⅱ）
10分
12分
19.（Ⅰ）证明：易证AD⊥面BB1C1C
∴面ADC1⊥面BB1C1C 4分
（Ⅱ）arcsin
8分
（Ⅲ）
12分
20.解：（Ⅰ）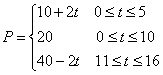
6分
（Ⅱ）
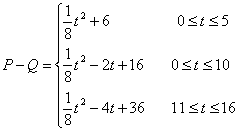10分
t=5时，Lmax=
，即第五个月销售利润最大. 12分
21.解：（Ⅰ）设P(x0,y0)是y=f(x)图象上点，Q（x,y）,则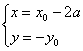
，
∴
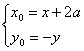∴－y=loga(x+2a－3a)，∴y=loga
(x＞a)
5分
（Ⅱ）
∴x＞3a
∵f(x)与g(x)在［a+2,a+3］上有意义.
∴3a＜a+2
∴0＜a＜1 6分
∵f(x)－g(x)≤1恒成立loga(x－3a)(x－a)≤1恒成立.
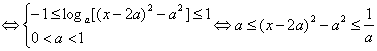8分
对x∈［a+2,a+3］上恒成立，令h(x)=(x－2a)2－a2
其对称轴x=2a,2a＜2,2＜a+2
∴当x∈［a+2,a+3］
hmin(x)=h(a+2)，hmax=h(a+3)
∴原问题等价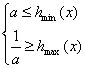
10分
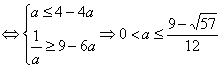12分
22.解：（Ⅰ）设椭圆E的方程为
(a＞b＞0)，由e=
∴a2=3b2
故椭圆方程x2+3y2=3b2 1分
设A(x1,y1)、B(x2,y2),由于点C（－1，0）分有向线段的比为2，
∴
|
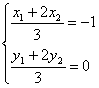
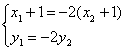3分
由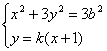
消去y整理并化简得
(3k2+1)x2+6k2x+3k2－3b2=0
由直线l与椭圆E相交于A（x1,y1）,B(x2,y2)两点
|
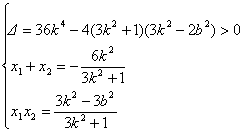5分
而S△OAB
⑥
由①④得:x2+1=－
，代入⑥得：S△OAB=
8分
（Ⅱ）因S△OAB=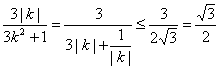
,当且仅当
S△OAB取得最大值 10分
此时x1+x2=－1,又∵
=－1
∴x1=1,x2=－2
将x1,x2及k2=
代入⑤得3b2=5
∴椭圆方程x2+3y2=5 14分