高三数学联考3
数学试卷
第一卷
一、选择题：
1．（文）已知集合A
｛1，2，3｝，且A中至少含有一个奇数，则这样的集合A有（ ）
A. 6个 B. 5个 C. 4个 D. 3个
（理）若ΔABC是锐角三角形，则复数Z=(
cosB-sinA)+i(sinB-cosA)对应点位于（ ）
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.已知正方体ABCD-A1B1C1D1，直线BC1与平面A1BD所成的角的余弦是（ ）
A.
B.
C.
D. 
3.若a=
+
+
+
+
+
+
+
+
+
+
+
且sin
=a
(
[0,
])，则tan
等于（ ）
A.
B.
或
C.
D.
4.在等比数列{an}中，设前n项和为Sn，则X=
+
，y=Sn(S2n+S3n)的大小关系是（ ）
A.x>y B.x=y C.x<y D.不确定
5．已知向量
=(2,2),
=(4,1)，在x轴上一点P使
有最小值，则P点的坐标是（ ）
A.(-3,0) B.(2,0) C.(3,0) D.(4,0)
6.已知f(x)=(x-a)(x-b)-2, m、n是方程f(x)=0的两根，且 a<b,m<n,则实数a、 b、 m 、n的大小关系是（ ）
A.m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
7．已知过球面上三点A、B、C的截面和球心的距离等于球半径R的一半，且AB=BC=CA=2，则球面积S=( )
A.
B.
C.4
D.
8.已知f(x)=αtan
-
sin
+4(其中
、为常数且ab
0),如果f(3)=5,则f(2004-3)的值为（ ）
A. -3 B. -5 C. 3 D.5
9．椭圆
+
=1上有n个不同的点P1，P2，…，Pn，椭圆的右焦点为F，数列{
}是公差大于
的等差数列，则n的最大值为（
）
A. 2001 B. 2000 C. 1999 D. 1998
10.一个凸多面体的顶点数为20，则它的各面多边形的内角总和为（ ）
A．5400° B. 6480° C. 7200° D. 7920°
11．对一切实数x，若二次函数f(x)=ax2+bx+c(a<b)的值恒为非负数，则M=
的最小值是（ ）
A. 3
B.2
C.
D.
12．由关于x的恒等式x4+a1x3+a2x2+a3x+a4=(x+1)4+b1(x+1)3+b2(x+1)2+b3(x+1)+b4,定义映射f:(a1, a2, a3, a4)→(b1, b2, b3, b4),则f(4, 3, 2, 1) = ( )
A.(1, 2, 3, 4) B.(0, 3, 4, 0) C.(-1, 0, 2, -2) D.(0, -3, 4, -1)
二、填空题：
13．将一张坐标纸折叠一次，使得点（0，2）与点（-2，0）重合，且点（2003，2004）与点（m,n）重合，则n-m=__________
14，（理）
（
）=_________________.
(文)若Sn=,则S2004=_________________.
15，如果一个三位正整数a1a2a3满足a1<a2且a3<a2，则称这样的三位数为凸数（如120，363，374等），那么所有凸数的个数是_______________（用数作答）
16，如下图，在下列六个图形中，每个小四边形皆为全等的正方形，那么沿其正方形相邻边折叠，能够围成正方体的是_____________(要求：把你认为正确图形的序号都填上)
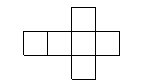
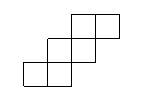
① ② ③
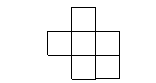
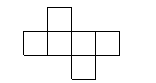
④ ⑤ ⑥
三．解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17．（本小题满分12分）甲、乙两个篮球运动员，投篮的命中率分别为0.6和0.8。如果每人投篮两次。
（1）求甲投进2球，且乙投进1球的概率；
（2）若投进1个球得2分，未投进得0分，求甲、乙两人得分相等的概率。
18．（本小题满分12分）已知数列{
}、{
}, 
，
分别表示{}、{}的前K项和（KN
），若
+=K
，又有
=
+
，求数列{
}的通项；欲使大于2004，正整数n至少取何值？
19．（本小题满分12分）已知S是
所在平面外一点，O是边AC的中点，
SOA=SOB=SOC，点P是SA的中点。
（1）求证：SO
平面ABC，
（2）求证：SC//平面BOP。
（3）若是等腰三角形，且AB=BC=a,又SC与平面BOP的距离为
a,求二面角B-SC-P的大小。
20．（本小题满分12分）已知f(x)=x3+ax2+bx+c,在x=1与x=-2时，都取得极值。
（1）求a,b的值；
（2）若x[-3,2]都有f(x)>
恒成立，求的取值范围。
21.
（本小题满分12分）已知函数f(x)=
(a、b、cN)，f(2)=2,f(3)<3,f(x)的图象按向量
=(-1,0)平移后得到的图象关于原点对称。
(1)求a、b、c的值；
（2）设0〈
〈1，0〈
1，求证
；
（3）设x是正实数，nN,求证
2n-2
22.（本小题满分14分）已知双曲线C的方程为
=1（a>0,b>0）,过右焦点F作双曲线在第一、第三象限的渐近线的垂线
，设垂足为P，且与双曲线C的左、右支的交点分别为A、B。
（1）求证：点P在双曲线C的右准线上；
（2）求双曲线C的离心率的取值范围；
（3）设=-1，
=-6，求双曲线C和直线的方程。
参考答案
一选择题BBCBC ADCBB AD
二填空题13、1。 14、（理）2，（文）
。 15、240。 16、①③⑥
三解答题
17、0.1512， 0.3924。
18、n至少取10
19、（3）600
20、a=,b=-6. 由f(x)min=-
+c>
-得
或
21、（1）a=1,b=1,c=0.
(2)
2。又
1 ∴
>2
又可证
，∴
（3）n=0,n=1时显然成立
时，
=
=
=
=2n-2
22、（1）P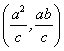
在右准线上
（2）e>
（3）由=-1得b2=6. 由=-1得x1x2+y1y2=-1
由根与系数的关系可求得a2=2,c=2∴双曲线方程
直线的方程y=-
.