高三数学练习(应用题)
一. 选择题:
1.某种放射性元素,100年后只剩原来质量的一半,现有这种元素1克,3年后剩下( )。
(A)![]() 克 (B)(1-0.5%)3克 (C)0.925克 (D)
克 (B)(1-0.5%)3克 (C)0.925克 (D)![]() 克
克
2.1980年我国工农业总产值为a亿元,到2000年工农业总产值实现翻两番的战略目标,年平均增长率至少达到( )。
(A)![]() -1 (B)
-1 (B)![]() -1 (C)
-1 (C)![]() -1 (D)
-1 (D)![]() -1
-1
3.某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘,根据需要,软件至少买3片,磁盘至少买2盒,则不同的选购方式共有( )。
(A)5种 (B)6种 (C)7种 (D)8种
4.已知函数y=2cosx (0≤x≤2π)的图象和直线y=2围成一个封闭的平面图形,则这个封闭图形的面积是( )。
(A)4 (B)8 (C)2π (D)4π
5.若干升水倒入底面半径为2cm的圆柱形容器中,量得水面的高度为6cm,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是 ( )。
(A)6![]() cm (B)6cm (C)2
cm (B)6cm (C)2![]() cm (D)3
cm (D)3![]() cm
cm

6.有一块“缺角矩形”地皮ABCDE,其尺寸如图,欲用此块地建一座地基为长方形的建筑物,以下四个方案中,哪一种地基面积最大( )。
(A) (B) (C) (D)
7.由甲城市到乙城市t分钟的电话费由函数g(t)=1.06×(0.75[t]+1)给出,其中t>0,[t]表示大于或等于t的最小整数,则从甲城市到乙城市5.5分钟的电话费为( )。
(A)5.83元 (B)5.25元 (C)5.56元 (D)5.04元
8.某商场卖甲、乙两种价格不同的商品,由于商品甲连续两次提价20%,同时商品乙连续两次季节性降价20%,结果都以每件23.04元售出,若商场同时售出这两种商品各一件,则与价格不升不降的情况比较,商场盈利的情况是( )。
(A)多赚5.92元 (B)多赚28.92元 (C)少赚5.92元 (D)盈利不变
9.有200根相同的钢管,把它们堆成三角形垛,使剩余的钢管尽可能少,那么剩余的钢管有( )。
(A)9根 (B)10根 (C)19根 (D)20根
10.某工厂生产总值月平均增长率为p,则年平均增长率为( )。
(A)p (B)12p (C)(1+p)12 (D)(1+p)12-1
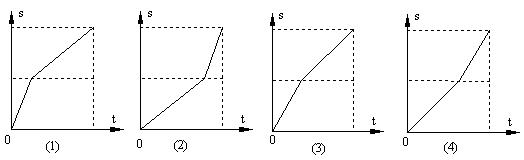
11.甲、乙两人同时从A地赶往B地,甲先骑自行车到中点改为跑步,而乙则是先跑步,到中点后改为骑自行车,最后两人同时到达B地,已知甲骑自行车比乙骑自行车快,若每人离开甲地的距离s与所用时间t的函数用图象表示,则甲、乙两人的图像分别是( )。
(A)甲是(1), 乙是(2) (B)甲是(1), 乙是(4)
(C)甲是(3), 乙是(2) (D)甲是(3), 乙是(4)
 |
12.某工厂在1990年底制订生产计划,要使得2000年底的总产值在原有基础上翻两番,则总产值的年平均增长率为( )。
(A)![]() -1 (B)
-1 (B)![]() -1 (C)
-1 (C)![]() -1 (D)
-1 (D)![]() -1
-1
二.填空题:
13.1999年11月1日起,全国储蓄存款征收利息税,利息税的税率为20%,即储蓄利息的20%由各银行储蓄点代扣代缴,某人在1999年11月1日存入人民币1万元,存期1年,年利率为2.25%,则到期可净得本金和利息总计 元。
14.某商品降价10%后,欲恢复原价,则应提价的百分数是 。
15.建造一个容积为8米3,深为2米的长方体无盖水池,如果池底和池壁的造价分别是每平方米120元和80元,那么水池的最低造价是 。
16.把一个小金属球表面涂漆,需要油漆0.15kg,将64个半径相同的小球熔化后,制成一个大金属球(设损耗为零),若对这个大金属球表面涂漆,需要油漆
kg.
三.解答题:
17.某车间生产某种产品,固定成本为2万元,每生产一件产品成本增加100元,已知总收益R(总收益指工厂出售产品的全部收入,它是成本与总利润的和,单位:元)是年产量Q(单位:件)的函数,满足关系式:
R=f(Q)=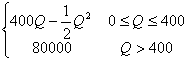 ,求每年生产多少产品时,总利润最大?此时总利润是多少元?
,求每年生产多少产品时,总利润最大?此时总利润是多少元?
18.在交通拥挤地段,为了确保交通安全,规定机动车相互之间的距离d(米)与车速v(千米/小时)需遵循的关系是d≥![]() (其中a(米)是车身长,a为常量),同时规定d≥
(其中a(米)是车身长,a为常量),同时规定d≥![]() ,(1)当d=
,(1)当d=![]() 时,求机动车车速的变化范围;
时,求机动车车速的变化范围;
(2)设机动车每小时流量Q=![]() ,应规定怎样的车速,使机动车每小时流量Q最大?
,应规定怎样的车速,使机动车每小时流量Q最大?
19.某地区原有森林木材存量为a,且每年的增长率为25%,因生产建设的需要,每年年底要砍伐的木材量为b,设an为n年后该地区的森林木材存量,
(1)求an的表达式;
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量应不少于![]() ,如果b=
,如果b=![]() a,那么该地区今后会发生水体流失吗?若会要经过几年?(取lg2=0.30)
a,那么该地区今后会发生水体流失吗?若会要经过几年?(取lg2=0.30)
 20.设某商店计划投入资金20万元经销甲或乙两种商品,已知经销甲商品与乙商品所获纯利润分别为P和Q(万元),且它们与投入资金x(万元)的关系是P=
20.设某商店计划投入资金20万元经销甲或乙两种商品,已知经销甲商品与乙商品所获纯利润分别为P和Q(万元),且它们与投入资金x(万元)的关系是P=![]() ,Q=
,Q=![]() (a>2),若不管如何投入,经销这两种商品或经销其中一种商品,所获纯利润总不少于5万元,试问a的最小值应是多少?
(a>2),若不管如何投入,经销这两种商品或经销其中一种商品,所获纯利润总不少于5万元,试问a的最小值应是多少?
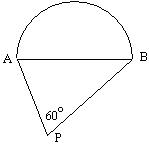
21.某建筑工地要挖一个横截面为半圆的柱形土坑,挖出的土只能沿AP、BP运到P处,其中AP=100米,BP=150米,∠APB=60°,请问怎样挖土才能最省工?
22.银行按规定在一定时间结算利息一次,结息后即将利息并入本金,这种计算方法叫做复利,现在某企业进行技术改造,有两种方案;甲方案:一次性贷款10万元,第一年可获利1万元,以后每年比前一年增加30%的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元。两种方案的贷款使用期都是10年,到期一次性还本付息,若银行贷款利率是按年息10%的复利计算,试比较两种方案的优劣(计算时精确到千元,并取1.110![]() 2.594,1.310
2.594,1.310![]() 13.79).
13.79).
参 考 答 案
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | C | D | B | A | A | C | B | D | B | B |
二.填空题:
| 13 | 10180 | 14 |
|
| 15 | 1760 | 16 | 4 |
三.解答题:
17.y=R-100Q-20000=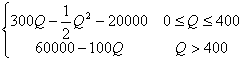 (Q∈Z),每年生产300件时利润最大,最大值为25000元。
(Q∈Z),每年生产300件时利润最大,最大值为25000元。
18.
(1) ![]() =
=![]() av2,
v=25
av2,
v=25![]() , ∴
0<v≤25
, ∴
0<v≤25![]() ,
,
(2) 当v≤25![]() 时, Q=
时, Q=![]() , Q是v的一次函数,v=25
, Q是v的一次函数,v=25![]() ,Q最大为
,Q最大为![]() ,当v>25
,当v>25![]() 时, Q=
时, Q=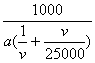 ≤
≤![]() , ∴当v=50时Q最大为
, ∴当v=50时Q最大为![]() .
.
19.(1)
an=(![]() )na-4[(
)na-4[(![]() )n-1]b,
(2) 8年后开始水土流失.
)n-1]b,
(2) 8年后开始水土流失.
20.总利润y=![]() , y≥5,
则
, y≥5,
则![]() ≥5, ∴
≥5, ∴ ![]() ≥10-
≥10-![]() ,
,
∴ a≥![]() , 该式对0≤x≤20恒成立,
, 该式对0≤x≤20恒成立,![]() 的最大值为
的最大值为![]() ,此时x=0,
,此时x=0,
∴ a的最小值为![]() .
.
21.设M是分界线上任意一点,∴ MA+AP=MB+PB,
∴MA-MB=PB-AP=50, ∴ 点M在以A、B为焦点的双曲线的右支上,
AB2=17500, 双曲线的方程是![]() , ∴运土时在双曲线弧左侧的土沿AP运到P处,右侧的土沿BP运到P处。
, ∴运土时在双曲线弧左侧的土沿AP运到P处,右侧的土沿BP运到P处。
22.甲方案:10年共获利42.63万元,银行贷款本息共25.94万元,净收益为16.7万元; 乙方案:10年共获利32.5万元,银行贷款本息共15.94万元,净收益为16.6万元; 所以,甲方案优于乙方案。