高三数学模拟试卷（六）
姓名 得分
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．若直线x+2ay－1＝0与直线（3a－1）x－ay－1＝0平行，则a等于（ ）．
A．
B．
C．0或 D．0或
2．已知映射f：A→B，其中A＝B＝R．对应法则f：x→y＝
．若对实数
，在集合A中不存在原像．则k的取值范围是（ ）．
A．k≤1 B．k<1 C．k≥1 D．k>1
3．实数a、b、c．满足a－c<b，则下列不等式中成立的是（ ）．
A．a>b－c B．a<b+c C．a>c－b D．a<b+c
4．如果点（5，b）在两条平行直线6x－8y+1＝0和3x－4y+5＝0之间，则b应取的整数值为（ ）．
A．5 B．－5 C．4 D．－4
5．若点F1、F2为椭圆
的焦点，P为椭圆上的点，当△F1PF2的面积为1时，
的值为（ ）．
A．0 B．1 C．3 D．6
6． 已知数列仙{
}中，
，则a10的值为（ ）．
A．28 B．33 C．
D．
7．已知
为锐角，
，则y与x的函数关系为（ ）
（A）
（B）
（C）
（D）
8．若连结双曲线
的四个顶点的四边形的面积为S1，连结它们的四个焦点的四边形的面积为S2，则之的最大值是（ ）．
A．
B．
C．2 D．
9．在三棱锥P—ABC中，M，N分别是PB、PC的中点，若截面AMN⊥面PBC，此棱锥侧面积与底面积的比为（ ）．
A．1：
B．
：
C．： D．
：1
10．—个盒子里装有相同大小的红球32个，白球4个，从中任取两个，则概率为
的事件是（ ）．
A．没有白球 B．至少有一个是红球 C．至少有一个是白球 D．至多有一个是白球
11．在地球北纬60°圈上有A、B两点．它们的经度相差180°，则A、B两点沿纬度圈的弧长与A、B两点间的球面距离之比为（ ）．
A．3：2 B．2：3 C．1：3 D．3：1
12．定义在R上的偶函数
满足
上是减函数，又α、β是锐角三角形的两内角，则下列结论中正确的是（ ）．
A.
B.
C．
D．
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．
13．若关于x的不等式
的解集为
，则实数m的值为__________。
14．点P在曲线
上移动，设过点P的切线的倾斜角为α，则α的取值范围是
.
15．已知函数是偶函数，且在（一∞，c）上为增函数，又f（－3）＝0，则满足
的x的取值范围是_________。
16．给出下列四个命题：
①若
②若
；③在△ABC中，a＝5，b＝8，c＝7，则＝20；④设A（4，a），B（b，8），C（a，b），若OABC是平行四边形（O为原点），则∠AOC＝
．其中真命题的序号是
.
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤
17．（本小题满分12分）
有一批食品出厂前，要进行五项指标抽检，如果有两项指标不合格，则这批食品不能出厂．已知每项指标抽检是相互独立的，且每项抽检出现不合格的概率都是0.2．
（Ⅰ）求这批食品不能出厂的概率（保留三位有效数字）；
（Ⅱ）求直至五项指标全部检验完毕，才能确定该批食品是否出厂的概率（保留三位有效数字）．
18．（本小题满分12分）
设一次函数f（x）的图像关于直线y＝x对称的图像为C，且f（－1）＝0．若点
在曲线C上，并有a1＝a2＝1．
（Ⅰ）求曲线C的方程；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）设
的值．
（文科生不作第（Ⅲ）问）
注意：考生在（19甲）、（19乙）两题中选一题作答，如果两题都答，只以（19甲）计分．
19．（甲）（本小题满分12分）
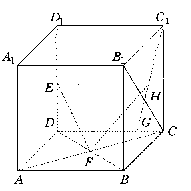
如图，在棱长为1的正方体ABCD—A1B1C1D1中，E、F分别是D1D、DB的中点，G在棱CD上．CG=
CD，H是C1G的中点，用向量方法解决下列问题：
（Ⅰ）求证：EF⊥B1C；
（Ⅱ）求EF与C1G所成角的余弦值；
（Ⅲ）求FH的长．
（乙）（本小题满分12分）
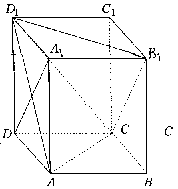
如图，在直四棱柱ABCD—A1B1C1D1中，底面是边长为a的菱形，侧棱长为2a．
（Ⅰ）问B1D1：与A1D能否垂直?并证明你的结论；
（Ⅱ）若∠ABC＝
，求二面角D1－AC－B1的大小；
（Ⅲ）当∠ABC在[，
]上变化时，求异面直线AC1与A1B1所成角的取值范围．
20．（理）（本小题满分12分）
设f（x）是定义在[－1，1]上的偶函数，f（x）与g（x）的图像关于x－1＝0对称，且当
[2，3]时，g（x）＝a（x－2）－2（x－2）3（a为常数）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若f（x）在[0，1]上是增函数，求实数a的取值范围；
（Ⅲ）若
（－6，6），问能否使f（x）的最大值为4．
（文）已知函数
的反函数是f（x）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若f（x）<f（1），求x的取值范围；
（Ⅱ）判断f（3）与3f（1）的大小关系，并加以证明．
21．（本小题满分12分）
已知双曲线
的左、右焦点分别为F1、F2，点P在双曲线的右支上，且：PF1＝3PF2．
（Ⅰ）求离心率e的最值，并写出此时双曲线的渐近线方程；
（Ⅱ）若当点P的坐标为（
）时，
．求双曲线的方程．
22．（理）（本小题满分14分）已知函数
的反函数为f（x）．
（Ⅰ）若f（x）<f（1），求x的取值范围；
（Ⅱ）判断f（2）与2f（1）；f（3）与3f（1）的大小关系，并加以证明；
（Ⅲ）请你根据（Ⅱ）归纳出一个更一般的结论，并给予证明．
（文）设f（x）是定义在[－1，1）上的偶函数，f（x）与g（x）的图像关于直线x－1＝0对称，且当[2，3]时，g（x）＝a（x－2）－2（x－2）3（a为常数）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若f（x）在[0，1]上是增函数，求实数a的取值范围；
（Ⅲ）若（一6，6），问能否使f（x）的最大值为4．
参考答案
第1卷
一、选择题
1．D 2．B 3．B 4．C 5．A 6．C
7．A 8．A 9．D 10．C 11．A 12．A
第Ⅱ卷
二、填空题
13．114．（理）
（文）3x+3y－2=0
15．（－3，0）
（3，+∞）16．②④
三、解答题
17．（Ⅰ）这批食品不能出厂的概率是：
（Ⅱ）五项指标全部检验完毕，这批食品可以出厂的概率是：
五项指标全部检验完毕，这批食品不能出厂的概率是：
由互斥事件有一个发生的概率加法公式可知，五项指标全部检验完毕，
才能确定这批食品出厂与否的概率是：
18．（Ⅰ）设f（x）＝ax+b（a≠0），则c的方程为：
①
由点（2，
）在曲线c上，得1＝
（2一b）． ②
由①②解得a＝b＝1，∴曲线c的方程为y＝x－1．
（Ⅱ）由，点（n+1，
）底曲线c上，有＝n
于是
．
·…·
，
即
注意到a1＝1，所以an＝（n－1）!
（Ⅲ）
∴
．
19．（甲）（Ⅰ）选取DA1、DC、DD1，分别为Ox、Oy、Oy轴建立空间直角坐标，易知E（0，0，
），F（，，0），B1（1，1，1），C（0，1，0），
，
＝0，
．
（Ⅱ）G（0，
，－1），Cl（0，1，1），
．
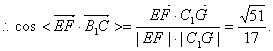（Ⅲ）
，
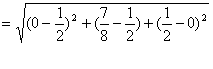
（乙）
（Ⅰ）用反证法易证B1D1与A1D不垂直．
（Ⅱ）由余弦有cos∠AC1D1=
设AC1=x，则
上
单调递增．
（Ⅲ）∵A1B1∥C1D1，∴∠AC1D1为异面直线AC1与A1B1所成角．
由余弦定理，有
设AC1＝x，则
故AC1与A1B1所成角的取值范围是
20．（理）解：
（Ⅰ）∵f（x）与g（x）的图像关于直线x－1＝0对称，
∴f（x）＝g（2－x）．
，
f（x）＝g（2一x）＝－ax+2x3．
又f（x）是偶函数，∴
f（x）=f（－x）＝ax一2x3．
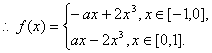
（Ⅱ）f（x）＝a－6x2，∵f（x）为[0，1]上的增函数．
∴f'（x）＝a－6x2≥0，
∴a≥6x2在
上，恒成立．
∵x
[0，1）时，6x2≤6，∴a≥6．
即a的取值范围是[6，+∞）．
（Ⅲ）当a在[0，1）上的情形．
由f'（x）=0，得
得a=6．此时x＝1
∴当a（－6，6）时，f（x）的最大值不可能是4．
（文）
（1）
（2）根据题意可得
，
整理得（ax－a）（ax+a－1）<0．
由于a>1，所以x<1．
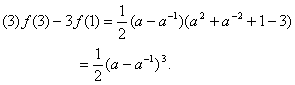
即
．
21．解：
（Ⅰ）∵PF1一PF2=2a，又PF1＝3PF2．
∴PF1＝3a，PF2＝a．
设F1（－c，0），F2（c，0），P（x0，y0），由
得3a=ex0+a，则x0=
．
∵P在双曲线右支上，∴x1≥a，即≥a，解得
1<e≤2．
∴e的最大值为2，此时
∴渐近线方程为
，
（Ⅱ）
．
又
．
∴
．
又
．
．
∴b2=C2－a2＝6．
∴双曲线方程为
．
22．（理）解：
（1）可求得f（x）＝
．
由f（x）<f（1）得．
整理得（ax－a）（ax+a—1）<0．
由于a>l，所以x<1．
（Ⅱ）
＝
,
由
，
，
即f（2）>2f（1）．
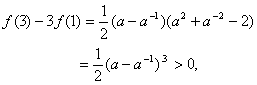
即f（3）>3f（1）．
（Ⅲ）更一般地，有：f（n）>nf（1） （n
*，n≥2）．
用数学归纳法证明，
①由（Ⅱ）知n＝2，3时，不等式成立．
②假设n＝k时，不等式成立，即f（k）>kf（1）．
．
这说明n＝k+1时，不等式也成立．
由①②可知，对于一切
，均有f（x）>nf（1）．
（文）解：
（Ⅰ）∵f（x）与g（x）的图像关于直线x－1＝0对称．
∴f（x）＝g（2－x），当x[－1，0]时，2一x[2，3]
f（x）＝g（2一x）＝一ax+2x3．
又∵f（x）是偶函数，∴x[0，1]时，一x[一1，0]
f（x）＝f（一x）＝ax一2x3．
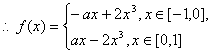
（Ⅱ）
上的增函数．
上恒成立
．
即a的取值范围是[6，+∞]．
（Ⅲ）只考虑在[0，1]上的情形．
由
．
∴当
的最大值不可能是4．