高三数学第二学期导师制（01）

高三数学第二学期导师制（01）

数学试卷

一、填空题

1.x∈R时，函数y=3sin()的周期是　　　   .

2．若，的夹角为30°，则的值为 　　　 .　　　　

3．在（1-x）⁵(1+x)⁴的展开式中x³的系数是 　　　　　 　.　　　　　　　　　　　　　

4.正六棱柱ABCDEF—A₁B₁C₁D₁E₁F₁的底面边长为1，侧棱长为，则这个棱柱的侧面对角线

E₁D与BC₁所成的角是 　　　　　　  .　　　

5．已知f(x)是一次函数，f(10)=21,且f(2), f(7),f(22)成等比数列，则f(1)+f(2)+…… +f(n)等于　　　　　　　　　　　 　.

6.2名医生和4名护士被分配到2所学校为学生体检，每校分配1名医生和2名护士，不同的分配方法共有 　　　　　　　　  .

7．一个工厂有若干个车间，今采用分层抽样方法从全厂某天的2048件产品中抽取一个容量为

128的样本进行质量检查，若某一车间这一天生产256件产品，则从这个车间抽取的产品件

数为_______。

8．若数列中，a₁=3, 且a_n+1=a_n²(n∈N^*)，则数列的通项a_n=___　　　___.

9. 直线与圆的位置关系是 　　　　　 .

10. 已知函数，则的值是　　　  .

11.若椭圆和双曲线有相同的焦点

，且P是两条曲线的一个交点，则的值为 　　　　　　  .

12.设集合S _n=，若X是S_n的子集，把X的所有数的乘积称为X的容量（若X中只有一个元素，则该元素的数值即为它的容量，规定空集的容量为0）。若X的容量为奇（偶）数，则称X为S_n的奇(偶)子集。若n=4，则S_n的所有奇子集的容量之和为__　　　 ___。

二、填空题　本大题共4小题，每小题4分，共16分。把答案填在题中横线上。

13.直线互相平行的一个充分条件是　　　　　　　　　　　　　　　 　　 （　　 ）

A．都平行于同一平面　　　　  B．与同一平面所成的角相等

C．所在的平面　　　　  D．都垂直于同一平面

14．设全集为R，对a>b>0，作集合M=，

则集合可表示为　　　　　　 　　　　　　　　　　　　　（　　 ）

A．M∪N　　 　　 B.M∩N　　　　 C.C_RM∩N　　　　D．M∩C_RN

15.已知非负实数x、y满足2x+3y－8≤0且3x+2y－7≤0 ，则x+y的最大值是　　（　　 ）

A． 　　　　　 B.　　　　　 C. 3　　　　　　 D.2

16．椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光

线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点A，B是它的

两个焦点，长轴长为2a，焦距为2c，静放在点A的小球（小球的半径不计），从

点A沿直线出发，经椭圆壁反弹后第一次回到点A时，小球经过的路程是　　（　　　）

A．4a　　　B．2(a－c)　　　C．2(a+c)　　　 D．以上答案均有可能

三、解答题

17．在△ABC中，a, b,c分别为角A、B、C的对边，且满足4sin².

(I)求角A的度数；　　（II）若a=, b+c=3,且b<c，求b, c的值。

解：

 

18．如图，已知斜三棱柱ABC—A₁B₁C₁中，∠BCA=90°，AC=BC=a，点A₁在底面ABC上的射影

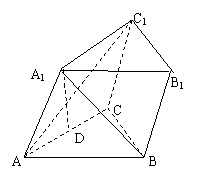恰为AC的中点D，BA₁⊥AC₁。

（I）求证：BC⊥平面A₁ACC₁；　

（II）求点A₁到AB的距离

（III）求二面角B—AA₁—C的正切值　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　

解：

 

19．已知函数f(x)=3^x+k(k为常数)，A（－2k, 2）是函数y=f^－1（x）图象上的点。

（I）求实数k的值及函数y=f^－1(x)的解析式；

（II）将y=f^－1(x)的图象按向量（3，0）平移，得到函数y=g(x)的图象。

若2f^－1(x+)－g(x)≥1恒成立，试求实数m的取值范围。

解：

20．设G、M分别为不等边△ABC的重心与外心，A（－1，0）、B（1，0），GM//AB。

（1）求点C的轨迹方程；

（2）设点C的轨迹为曲线E，是否存在直线，使过点（0.1）并与曲线E交于P、Q两点，且满足？若存在，求出直线的方程，若不存在，说明理由。

注：三角形的重心的概念和性质如下：设△ABC的重心，且有。

解：

 

高三数学第二学期导师制（01）

数学试卷答案

一、填空题

1.x∈R时，函数y=3sin()的周期是　4  .

2．若，的夹角为30°，则的值为  　.　　　　

3．在（1-x）⁵(1+x)⁴的展开式中x³的系数是  4 　.　　　　　　　　　　　　　

4.正六棱柱ABCDEF—A₁B₁C₁D₁E₁F₁的底面边长为1，侧棱长为，则这个棱柱的侧面对角线

E₁D与BC₁所成的角是 60° .　　　

5．已知f(x)是一次函数，f(10)=21,且f(2), f(7),f(22)成等比数列，则f(1)+f(2)+…… +f(n)等于 n²+2n 　.

6.2名医生和4名护士被分配到2所学校为学生体检，每校分配1名医生和2名护士，不同的分配方法共有 12种  .

7．一个工厂有若干个车间，今采用分层抽样方法从全厂某天的2048件产品中抽取一个容量为

128的样本进行质量检查，若某一车间这一天生产256件产品，则从这个车间抽取的产品件

数为____16____。

8．若数列中，a₁=3, 且a_n+1=a_n²(n∈N^*)，则数列的通项a_n=__ 3^2n－1 ____.

9. 直线与圆的位置关系是  相交   .

10. 已知函数，则的值是　3   .

11.若椭圆和双曲线有相同的焦点

，且P是两条曲线的一个交点，则的值为 　 　.

12.设集合S _n=，若X是S_n的子集，把X的所有数的乘积称为X的容量（若X中只有一个元素，则该元素的数值即为它的容量，规定空集的容量为0）。若X的容量为奇（偶）数，则称X为S_n的奇(偶)子集。若n=4，则S_n的所有奇子集的容量之和为___7___。

二、填空题　本大题共4小题，每小题4分，共16分。把答案填在题中横线上。

13.直线互相平行的一个充分条件是　　　　　　　　　　　　　　　　　  （ D　 ）

A．都平行于同一平面　　　　  B．与同一平面所成的角相等

C．所在的平面　　　　  D．都垂直于同一平面

14．设全集为R，对a>b>0，作集合M=，

则集合可表示为　　　　　　　　　　　　　　　　　　 　（ D　 ）

A．M∪N　　 　　 B.M∩N　　　　 C.C_RM∩N　　　　D．M∩C_RN

15.已知非负实数x、y满足2x+3y－8≤0且3x+2y－7≤0 ，则x+y的最大值是　　（　C  ）

A． 　　　　　 B.　　　　　 C. 3　　　　　　 D.2

16．椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点A，B是它的两个焦点，长轴长为2a，焦距为2c，静放在点A的小球（小球的半径不计），从点A沿直线出发，经椭圆壁反弹后第一次回到点A时，小球经过的路程是　　　　　　　　　　　　　　  （ D　）

A．4a　　　B．2(a－c)　　　C．2(a+c)　　　 D．以上答案均有可能

 

三、解答题（本大题共6小题，共74分。解答应写出必要的文字说明、证明过程或演算步骤。）

17．在△ABC中，a, b,c分别为角A、B、C的对边，且满足4sin².

(I)求角A的度数；　　（II）若a=, b+c=3,且b<c，求b, c的值。

解：（I）由4sin²

即4cos²A－4cosA+1=0得cosA=,∴A=60°

（II）由余弦定理有a²=b²+c²－2bc cosA. 又a=得3=（b+c）²－2bc－2bccosA，解得bc=2,………………10分　　联立方程组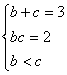解得b=1，c=2…………12分

18．如图，已知斜三棱柱ABC—A₁B₁C₁中，∠BCA=90°，AC=BC=a，点A₁在底面ABC上的射影

恰为AC的中点D，BA₁⊥AC₁。

（I）求证：BC⊥平面A₁ACC₁；　（II）求点A₁到AB的距离

（III）求二面角B—AA₁—C的正切值　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

解：（1）由题意，A₁D⊥平面ABC，∴A₁D⊥BC。

又AC⊥BC，∴BC⊥平面A₁ACC₁

（II）过D作DH⊥AB于H，又A₁D⊥平面ABC，∴AB⊥A₁H

∴A₁H是H₁到AB的距离

∵BA₁⊥AC₁，BC⊥平面A₁ACC₁，由三垂线定理逆定理，得A₁C⊥AC₁

∴　A₁ACC₁是菱形　　  ∴A₁A=AC=a, A₁D=.

由Rt△ADH～Rt△ABC，可得DH=　　  在Rt△A₁DH中，求得A₁H=为所求距离。

（III）过C作CM⊥AA₁于M，则正△AA₁C中，M为AA₁中点

∵BC⊥平面A₁ACC₁，由三垂线定理，得AA₁⊥BM。

∴∠BMC是二面角B—AA₁—C的平面角。　 ∵CM=，BC=a,

tg∠BMC=

19．（本小题满分12分）

已知函数f(x)=3^x+k(k为常数)，A（－2k, 2）是函数y=f^－1（x）图象上的点。

（I）求实数k的值及函数y=f^－1(x)的解析式；

（II）将y=f^－1(x)的图象按向量（3，0）平移，得到函数y=g(x)的图象。

若2f^－1(x+)－g(x)≥1恒成立，试求实数m的取值范围。

解：（I）∵A（－2k, 2）是函数y=f^－1(x)图象上的点。

∴B（2，－2K）是函数y=f(x)上的点。　　 ∴2k=3²+k

∴k=－3, ∴y=f(x)=3^x－3　　　　　 ∴y=f^－1(x)=log₃(x+3),(x>－3)

（II）将y=f^－1(x)的图象按向量=（3，0）平移，得函数y=g(x)=log₃x(x>0)

要使2f^－1(x+)－g(x)≥1 恒成立，　 即使2log₃(x+)－log₃­x≥1恒成立。

所以有x+≥3在x>0时恒成立，只须（x+）_min≥3。

又x+(当且仅当x=时取等号)

∴（x+）_min=4　　　　　  只须4≥3，即m≥。

∴实数m的取值范围为

20．本小题满分12分

设G、M分别为不等边△ABC的重心与外心，A（－1，0）、B（1，0），GM//AB。

（1）求点C的轨迹方程；

（2）设点C的轨迹为曲线E，是否存在直线，使过点（0.1）并与曲线E交于P、Q两点，且满足？若存在，求出直线的方程，若不存在，说明理由。

注：三角形的重心的概念和性质如下：设△ABC的重心，且有。

解：(I)点C的轨迹方程为 x²+

(II)假设存在直线满足条件，设直线方程为y=kx+1,

由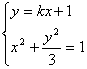消去x，得（3+k²）x²+2kx－2=0

∵直线与曲线E并于P、Q两点，∴△=4k²+8(2+k²)>0

设P(x₁,y₁)，Q（x₂,y₂）,则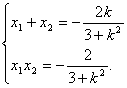

∵

∴x₁x₂+y₁y₂=－2,即x₁x₂+(kx₁+1)(kx₂+1)=－2.

(1+k²)x₁x₂+k(x₁+x₂)+3=0, (1+k²)

解得k²=7, ∴k=±

故存在直线：y=±+1,使得