高三数学第二学期导师制（02）
班级 姓名 成绩
一、填空题
1．已知集合
，则实数a的
取值范围是 。
2．在数列
，则该数列中相邻两项的乘积是负数的
是 。
3．要使函数
上存在反函数，则a的取值范围是
。
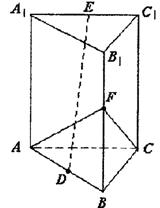
4．已知长方体ABCD－A1B1C1D1中，AB=BC=4，CC1=2，则直线BC1和平面DBB1D1所成角的正弦
值为 。
5、若把抛物线y=2x2绕其顶点逆时针方向转动90°，则转动后所得的抛物线的焦点坐标为 。
6、设 ABCD的对角线交于点O，且
，
，则
=
。
7、某校准备召开高中毕业生代表会，把6个代表名额分配给高三年级的3个班，每班至少一个
名额，不同的分配方案共有 种。
8、已知函数f(n)=
(n∈N)，则
= 。
9．当
=
.
10．不等式
的解集为 .
11．设a、b是方程
的两个不相等的实数根，那么过点A（a,a2）和
B（b，b2）的直线与圆
的位置关系是 。
12．对于项式
，四位同学作出了四种判断：
①存在n∈N+，展开式中有常数项；②对任意n∈N+，展开式中没有常数项；
③对任意n∈N+，展开式中没有x的一次项；④存在n∈N+，展开式中有x的一次项.
上述判断中正确的是 。
二、填空题（每小题4分，共16分）
13．
2的必要非充分条件是 （
）
A．
B．
C．
D．
14、对函数f(x)=a2+bx+c(a≠0)作x=h(t)的代换，则不改变函数f(x)值域的代换是 （ ）
A、h(t)=10t B、h(t)=t2 C、h(t)=sint D、h(t)=log2t
15、样本a1，a2，a3，…，a10的平均数为
，样本b1，b2，…，b10的平均数为
，
那么样本a1，b1，a2，b2，a3，b3，…，a10，b10的平均数是 （ ）
A、+ B、
(+) C、2(+) D、
(+)
16．已知定义在R上的函数y=f(x)满足下列三个条件：①对任意的x∈R都有
②对于任意的
，都有
③
的图象关于y轴对称，则下列结论中，正确的是 （ ）
A．
B．
C．
D．
三、解答题（本大题共6小题，共74分）
17．（本题满分12分）
|
（1）求此三棱柱的高；
（2）求二面角C—AF—B的大小.
18．（本题满分12分）
已知向量
=（2，2），向量
与向量的夹角为
，且·=-2，
（1）求向量；
（2）若
，其中A、C是△ABC的内角，若三角形的三内角A、B、C依次成等差数列，试求+
的取值范围.
解：
19、甲、乙两人用农药治虫，由于计算错误，在
、
两个喷雾器中分别配制成12%和6%的药水各10千克，实际要求两个喷雾器中的农药的浓度是一样的，现在只有两个容量为1千克的药瓶，他们从、两个喷雾器中分别取1千克的药水，将中取得的倒入中，中取得的倒入中，这样操作进行了
次后，喷雾器中药水的浓度为
%，喷雾器中药水的浓度为
%．
（Ⅰ）证明
是一个常数；（Ⅱ）求与
的关系式；（Ⅲ）求的表达式．
解：
20、设函数
的定义域是R，对于任意实数
，恒有
，且当
时，
．
（Ⅰ）求证：
，且当
时，有
；
（Ⅱ）判断在R上的单调性；
（Ⅲ）设集合
，集合
，若
，求
的取值范围．
解：
高三数学第二学期导师制（02）解答
一、填空题
1．已知集合，则实数a的
取值范围是（－1，2）。
2．在数列，则该数列中相邻两项的乘积是负数的
是 a23·a24。 。
3．要使函数上存在反函数，则a的取值范围是
或
。
4．已知长方体ABCD－A1B1C1D1中，AB=BC=4，CC1=2，则直线BC1和平面DBB1D1所成
角的正弦值为 
。
5、若把抛物线y=2x2绕其顶点逆时针方向转动90°，则转动后所得的抛物线的焦点坐标为
(
，0) 。
6、设 ABCD的对角线交于点O，且，，则=
。
7、某校准备召开高中毕业生代表会，把6个代表名额分配给高三年级的3个班，每班至少一个名额，不同的分配方案共有 10 种。
8、已知函数f(n)=(n∈N)，则= 1 。
9．当=
2 .
10．不等式的解集为 
.
11．设a、b是方程的两个不相等的实数根，那么过点A（a,a2）和
B（b，b2）的直线与圆的位置关系是 相交 。
12．对于项式，四位同学作出了四种判断：
①存在n∈N+，展开式中有常数项；②对任意n∈N+，展开式中没有常数项；
③对任意n∈N+，展开式中没有x的一次项；④存在n∈N+，展开式中有x的一次项.
上述判断中正确的是 ④与① 。
二、填空题（每小题4分，共16分）
13．2的必要非充分条件是 （ A ）
A． B． C． D．
14、对函数f(x)=a2+bx+c(a≠0)作x=h(t)的代换，则不改变函数f(x)值域的代换是（ D ）
A、h(t)=10t B、h(t)=t2 C、h(t)=sint D、h(t)=log2t
15、样本a1，a2，a3，…，a10的平均数为，样本b1，b2，…，b10的平均数为，
那么样本a1，b1，a2，b2，a3，b3，…，a10，b10的平均数是 （ B ）
A、+ B、(+) C、2(+) D、(+)
16．已知定义在R上的函数y=f(x)满足下列三个条件：①对任意的x∈R都有②对于任意的，都有③的图象关于y轴对称，则下列结论中，正确的是 （ B ）
A． B．
C． D．
三、解答题（本大题共6小题，共74分）
17．（本题满分12分）
|
（1）求此三棱柱的高；
（2）求二面角C—AF—B的大小.
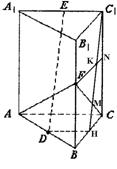
17．解：（1）取BC、C1C的中点分别为H、N，连结HC1，
连结FN，交HC1于点K，则点K为HC1的中点，因
FN//HC，则△HMC∽△FMK，因H为BC中点
BC=AB=2，则KN=
，∴
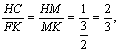
则HM=
，在Rt△HCC1，HC2=HM·HC1，
解得HC1=
，C1C=2.
另解：取AC中点O，以OB为x轴，OC为y轴，按右手系建立空间坐标系，设棱柱高为h，则C（0，1，0），F（
），D（
），E（0，0，h），∴
，由CF⊥DE，得
，解得h=2.
|
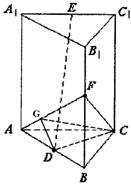
由三垂线定理得CG⊥AF，所以∠CGD是二面角C—AF—B
的平面角，又在Rt△AFB中，AD=1，BF=1，AF=
，
从而DG=
∴tan∠CGD=
，
故二面角C—AF—B大小为arctan
.
18．（本题满分12分）
已知向量=（2，2），向量与向量的夹角为，且·=-2，
（1）求向量；
（2）若，其中A、C是△ABC的内角，若三角形的三内角A、B、C依次成等差数列，试求+的取值范围.
18．解：（1）设
=（x,y），则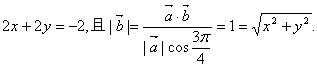
∴解得
（2）
. ∴
∴
=1+
∴
∴
19、本小题满分12分
甲、乙两人用农药治虫，由于计算错误，在、两个喷雾器中分别配制成12%和6%的药水各10千克，实际要求两个喷雾器中的农药的浓度是一样的，现在只有两个容量为1千克的药瓶，他们从、两个喷雾器中分别取1千克的药水，将中取得的倒入中，中取得的倒入中，这样操作进行了次后，喷雾器中药水的浓度为%，喷雾器中药水的浓度为%．
（Ⅰ）证明是一个常数；（Ⅱ）求与的关系式；（Ⅲ）求的表达式．
19、解：（1）开始时，中含有10
12%＝1.2千克的农药，中含有106%＝0.6千克的农药，次操作后，中含有10%＝0.1千克的农药，中含有10%＝0.1千克的农药，它们的和应与开始时农药的重量和相等，从而有
，所以＝18（常数）--------------------4分
（2）第次操作后，中10千克药水中农药的重量具有关系式：
，
由（1）知
，代入化简得
① 
----------------------8分
(3)令
，利用待定系数法可求出
＝－9，-----------------9分
所以
，可知数列
是以
为首项，
为公比的等比数列，--10分
由①，
------------------------------11分
由等比数列的通项公式知：
，所以
．----12分
20、本小题满分12分
设函数的定义域是R，对于任意实数，恒有，且当 时，．
（Ⅰ）求证：，且当时，有；
（Ⅱ）判断在R上的单调性；
（Ⅲ）设集合，集合，若，求的取值范围．
解：(1)
，令
，则
，且由时，，所以；--------------------------------------2分
设
，
，
．-----4分
（2）
，则
时，
，----------------------------6分
，
在R上单调递减．-------------------------8分
（3）
，由单调性知
，---9分
又
，---------------------------------------10分
，
，
，从而
．---------12分