高三数学第二学期第一次月考
数学（文科）试卷
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项符合题目要求。
1．在函数
中，最小正周期为
的函数是（ ）
A. 
B. 
C. 
D. 
2．设
：
，
：
，则下列命题为真的是（ ）
A．若
则
B．若则 C．若则 D．若则
3．已知
的最大值为2，
的最大值为
，则的取值范围是（ ）
A．
B．
C．
D．以上三种均有可能
4．双曲线
的渐近线方程是（ ）
A. 
B. 
C. 
D. 
5．欲对某商场作一简要审计，通过检查发票及销售记录的2%来快速估计每月的销售总额。现采用如下方法：从某本50张的发票存根中随机抽一张，如15号，然后按序往后将65号，115号，165号，…发票上的销售额组成一个调查样本。这种抽取样本的方法是（ ）
A．简单随机抽样 B．系统抽样 C．分层抽样 D．其它方式的抽样
6．在抛物线
上，横坐标为4的点到焦点的距离为5，则p的值为（ ）
A. 
B.
1
C. 2
D. 4
7．数列
满足
并且
。则数列的第100项为（ ）
A．
B．
C．
D．
8．在长方体
中，
、
分别是棱
、
的中点，若
，则异面直线
与
所成的角为（ ）
A．
B．
C．
D．
9．若函数
的图象按向量
平移后，它的一条对称轴是
，则
的一个可能的值是（ ）
A．
B．
C．
D．
10． 在100件产品中有6件次品，现从中任取3件产品，恰有1件次品的不同取法的种数是（ ）
A. 
B. 
C. 
D. 
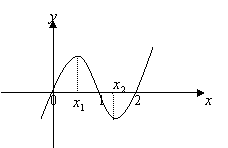11．如图是函数
的大致
图象，则
等于（ ）
A．
B．
C．
D．
12．椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点A，B是它的两个焦点，长轴长为2a，焦距为2c，静放在点A的小球（小球的半径不计），从点A沿直线出发，经椭圆壁反弹后第一次回到点A时，小球经过的路程是（ ）
A．4a B．2(a－c) C．2(a+c) D．以上答案均有可能
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
13．已知函数
，则方程
的解
__________.
14．过抛物线
的焦点
作垂直于
轴的直线，交抛物线于
、
两点，则以为圆心、
为直径的圆方程是________________.
15．某篮球运动员在罚球线投中球的概率为
，在某次比赛中罚3球恰好命中2球的概率为_____________.
16.一水池有2个进水口，1 个出水口，进出水速度如图甲、乙所示. 某天0点到6
点，该水池的蓄水量如图丙所示.（至少打开一个水口）
 |
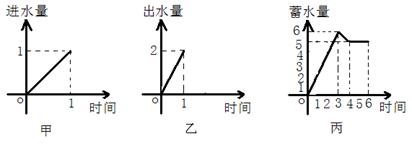给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水.则一定能确定正确的论断序号是_______________.
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）已知 
、
是夹角为600的两个单位向量，令向量
=2+， 
=－3+2.
（1）求向量的模；
（2）求向量与的夹角.
18．（本小题满分12分）在
中，
分别是
的对边长，已知成等比数列，且
，求
的大小及
的值.
19．（本小题满分12分）{
}、{
}都是各项为正的数列，对任意的
，都有、
、
成等差数列，、、
成等比数列.
(1) 试问{}是否为等差数列，为什么？
(2) 如
=1，
=
，求
；
20．（本小题满分12分）如图，四棱锥
的底面是边长为1的正方形，SD垂直
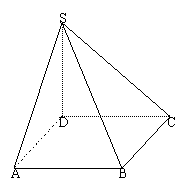于底面ABCD，
。
（1）求证
；
（2）求面ASD与面BSC所成二面角的大小；
21．（本小题满分12分）某服装厂生产一种服装，每件
服装的成本为40元，出厂单价定为60元。该厂为鼓励
销售商订购，决定当一次订购量超过100件时，每多订
购一件，订购的全部服装的出厂单价就降低0.02元。根
据市场调查，销售商一次订购量不会超过500件。
（I）设一次订购量为x件，服装的实际出厂单价为P元，写出函数
的表达式；
（II）当销售商一次订购了450件服装时，该服装厂获得的利润是多少元？
（服装厂售出一件服装的利润＝实际出厂单价－成本）
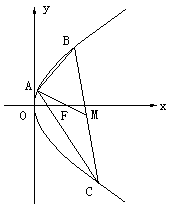
22．（本小题满分14分）已知点A（2，8），
在抛物线上，的重心与此抛物线的焦点F重合（如图）
（1）写出该抛物线的方程和焦点F的坐标；
（2）求线段BC中点M的坐标；
（3）求BC所在直线的方程。
参考答案（文科）
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | A | C | A | B | C | D | D | A | A | C | D |
二、填空题：
13．1 14．
15． 
16．①
三、解答题：
17．解：（1）
…6分.
（2）、同法得
， 
=－
，cos<,>=－
,<,>=1200 …… 12分.
18．解：（1）
成等比数列 
又
，在中，由余弦定理得
（2）在中，由正弦定理得
19．(1)依题意
(2分)
∴
∴{
}为等差数列 (6分)
(2)由
，
，求得
(8分)
∴
∴
(12分)
20．解：
底面ABCD，且ABCD为正方形
可以把四棱锥补形为长方体
，如图2
面ASD与面BSC所成的二面角就是面
与面
所成的二面角，
又
为所求二面角的平面角
在
中，由勾股定理得
在
中，由勾股定理得
即面ASD与面BSC所成的二面角为
21．（1）当
时，
当
时，
所以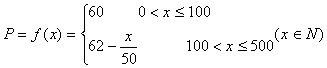
（2）设销售商的一次订购量为x件时，工厂获得的利润为L元，则
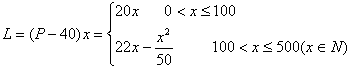
当
时，
因此，当销售商一次订购了450件服装时，该厂获利的利润是5850元。
22．（1）由点A（2，8）在抛物线上，有
解得
所以抛物线方程为
，焦点F的坐标为（8，0）
（2）如图，由F（8，0）是的重心，M是BC的中点，所以F是线段AM的定比分点，且
设点M的坐标为
，则
解得
所以点M的坐标为
（3）由于线段BC的中点M不在x轴上，所以BC所在的直线不垂直于x轴。
设BC所成直线的方程为 
由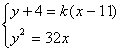
消x得 
所以
由（II）的结论得
解得
因此BC所在直线的方程为 
即