高三数学第五次月考数学试题
|
1.如果事件A、B互斥,那么
|
2.如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B)
|
|
次的概率 ![]()
一.选择题:(每题5分,共60分.在每小题给出的四个选项中,只有一项是符合
题目要求的请把答案填在答卷的答题表内).
1.设P={3,4,5},Q={4,5,6,7},定义P※Q=![]() ,则P※Q中元素个数( )
,则P※Q中元素个数( )
A.3个 B.4个 C.7个 D.12个
|
|
.
3.在数列![]() 则该数列中相邻两项的乘积是负数的是
则该数列中相邻两项的乘积是负数的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设p、q为简单命题,则“p且q”为假是“p或q”为假的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
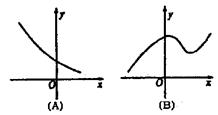
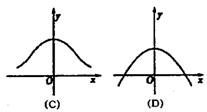
5.对于任意![]() 的值恒大于零,那么x的取值范围是( )
的值恒大于零,那么x的取值范围是( )
A.(1,3) B.![]() C.(1,2) D.
C.(1,2) D.![]()
|
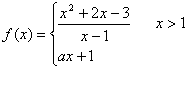 在点
在点A.2 B.3 C.-2 D.-4
(文)一个容量为20的样本数据,数据的分组及各组的频数如下:
(10,20),2;(20,30),3;(30,40),4;(40,50),5;(50,60),4;(60,70),2.
则样本在区间(-∞,50)上的频率为 ( )
A.0.5 B.0.7 C.0.25 D.0.05
7.设F1,F2是双曲线![]() 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且![]() ,
,
则![]() 的值等于 ( )
的值等于 ( )
A.2 B.![]() C.4 D.8
C.4 D.8
8-.已知a,b是两条直线,α,β是两个平面,有下列4个命题:
A.若a∥b,b![]()
![]() ,则a∥
,则a∥![]()
B.若a⊥b,a⊥![]() ,b
,b![]()
![]() ,则b∥
,则b∥![]()
C.若![]() ⊥
⊥![]() ,a⊥
,a⊥![]() ,b⊥
,b⊥![]() ,则a⊥b --
,则a⊥b --
D.若a,b异面,a![]()
![]() ,b
,b![]()
![]() ,a∥
,a∥![]() ,则
,则![]() ∥
∥![]()
其中正确命题有 ( )
A.①② B.②③ C.③④ D.②④
9.若x∈R、n∈N*,定义:![]() =(-5)(-4)
=(-5)(-4)
(-3)(-2)(-1)=-120,则函数![]() 的奇偶性为 ( )
的奇偶性为 ( )
A.是偶函数而不是奇函数 B.是奇函数而不是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
10.如果![]() 等于
等于
A.2003 B.1001
C.2004 D.2002
11. 一次文艺演出中,需给舞台上方安装一排彩灯共15只,以不同的点亮方式增加舞台效果,要求设计者按照每次点亮时,必须有6只是关的,且相邻的灯不能同时被关掉,两端的灯必须点亮的要求进行设计,那么不同点亮方式的种数是 ( )
A.28 B.84 C.180 D.360
12.某商场对顾客实行购物优惠活动,规定一次购物:(1)如不超过200元,则不予优惠;(2)如超过200元但不超过500元的按9折优惠;(3)如超过500元,其中500元按9折给予优惠,超过500元的部份给予8折优惠.某人两次去购物,分别付款168元和423元,若他只去一次购买同样价值的商品,则应付款 ( )
A.472.8元 B.510.4元 C.522.8元 D.560.4元
二.填空题(每题4分,共16分,把答案填在答卷横线上)
13.(理)设复数![]() 等于
(文)函数
等于
(文)函数![]() 单调减区间是 .
单调减区间是 .
14.函数![]() 的图象按向量
的图象按向量![]() 平移后成为某奇函数图象,使
平移后成为某奇函数图象,使![]() 最小
最小
的向量![]() 的坐标为
.
的坐标为
.
15.在一个水平放置的底面半径为![]() 的圆柱形量杯中装有适量的水,现放入下个半径为R的
的圆柱形量杯中装有适量的水,现放入下个半径为R的
实心铁球,球完全浸没于水中且无水溢出,若水面高度恰好上升R,则R=
16.(文科做)若在![]() 的展开式中,x的一次项是第6项,则n=
的展开式中,x的一次项是第6项,则n=
(理科做)函数![]() 在
在![]() 上的最大值是
.
上的最大值是
.
第五次月考数学试卷答卷
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
13 . _____________________ 14._________________________
15_______________________ 16._________________________
三.解答题(17-21每题12分,22题14分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)(文科做)某学生语、数、英三科考试成绩,在一次考试中排名全班第一的概率:语文为0.9,数学为0.8,英语为0.85,问一次考试中
(Ⅰ)三科成绩均未获得第一名的概率是多少?(Ⅱ)恰有一科成绩未获得第一名的概率是多少?
(理科做)摇奖器有10个小球,其中8个小球上标有数字2,2个小球上标有数字5,现摇出3个小球,规定所得奖金(元)为这3个小球上记号之和,求此次摇奖获得奖金数额的数学期望.
18.(本小题满分12分)
已知A、B、C的坐标分别为A(3,0),B(0,3),C(![]() ),
),![]()
(I)若![]() 求角
求角![]() 的值; (II)若
的值; (II)若![]() 的值.
的值.
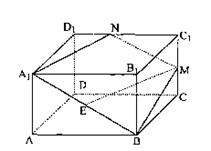
19.(本小题满分12分)
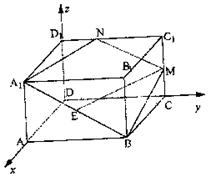
如图,在正四棱柱ABCD—A1B1C1D1中,AA1=![]() AB,点E、M分别为A1B、C1C的中点,
AB,点E、M分别为A1B、C1C的中点,
过点A1,B,M三点的平面A1BMN交C1D1于点N.
|
20. (本小题满分12分)
某银行准备新设一种定期存款业务,经预测,存款量与利率的平方成正比,
比例系数为K(K>0),贷款的利率为4.8%,又银行吸收的存款能全部放贷出去.
(1)若存款的利率为x,x![]() (0,0.048),试写出存款量g(x)及银行应支付给储户的利息h(x);
(0,0.048),试写出存款量g(x)及银行应支付给储户的利息h(x);
(2)存款利率定为多少时,银行可获得最大收益?
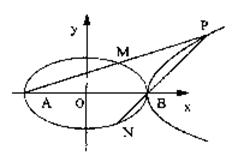
21.(本小题满分12分)已知椭圆![]() 的一条准线方程是
的一条准线方程是![]() 其左、右顶点分别是A、B;双曲线
其左、右顶点分别是A、B;双曲线![]() 的一条渐近线方程为3x-5y=0.
的一条渐近线方程为3x-5y=0.
(Ⅰ)求椭圆C1的方程及双曲线C2的离心率;
(Ⅱ)在第一象限内取双曲线C2上一点P,连结AP交椭圆C1于点M,
|
22. (本小题满分14分)已知函数f(x)=a0+a1x+a2x2+a3x3+……+anxn(n![]() N*),且y= f(x)的
N*),且y= f(x)的
图象经过点(1,n2),数列{an}(n![]() N*)为等差数列。
N*)为等差数列。
(1)求数列{an}通项公式;
(2)当n为奇数时,设g(x)=![]() [ f(x)- f(-x)],是否存在自然数m和M,使不等式
[ f(x)- f(-x)],是否存在自然数m和M,使不等式
m<g(![]() )<M恒成立,若存在,求出M-m的最小值;若不存在,说明理由。
)<M恒成立,若存在,求出M-m的最小值;若不存在,说明理由。
第五次月考试题参考答案
1-5DCCBB 6-10 B(文B)ABAC 11-12 AD 13.理![]() 文(-2,2)
文(-2,2)
14.(![]() ) 15.R=
) 15.R=![]() 16.文 n=8 理 1
16.文 n=8 理 1
17.(文科)解:分别记该生语、数、英考试成绩排名全班第一的事件为A、B、C,
则P(A)=0.9 P(B)=0.8,P(C)=0.85 …………………………2分
(Ⅰ)![]()
=[1-P(A)]·[1-P(B)]·[1-P(C)]
=(1-0.9)×(1-0.8)×(1-0.85)
=0.003
答:三科成绩均未获得第一名的概率是0.003………………6分
(Ⅱ)P(![]() )
)
= P(![]()
=![]()
=[1-P(A)]·P(B)·P(C)+P(A)·[1-P(B)]·P(C)+P(A)·P(B)·[1-P(C)]
=(1-0.9)×0.8×0.85+0.9×(1-0.8)×0.85+0.9×0.8×(1-0.85)
=0.329
答:恰有一科成绩未获得第一名的概率是0.329……………………12分
(理科)设此次摇奖的奖金数额为ξ元,当摇出的3个小球均标有数字2时,ξ=6;当摇出的3个小球中有2个标有数字2,1个标有数字5时,ξ=9;当摇出的3个小球有1个标有数字2,2个标有数字5时,ξ=12。
所以,![]()
![]()
![]() ………9分
………9分
Eξ=6×![]() (元)
(元)
答:此次摇奖获得奖金数额的数字期望是![]() 元 ……………………12分
元 ……………………12分
18.(本小题满分12分)
解:(1)![]() ,…………2分
,…………2分
![]() ,
,
![]() .……………………4分
.……………………4分
由![]() 得
得![]() .
又
.
又![]() .…………6分
.…………6分
(2)由![]()
![]() ①………………7分
①………………7分
又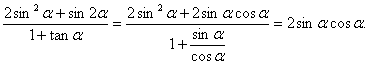 ………………9分
………………9分
由①式两分平方得![]()
![]() ……………………12分
……………………12分
19.(A)(Ⅰ)证明:取A1B1的中点F,连EF,C1F
∵E为A1B中点
∴EF∥ ![]() BB1…………2分
BB1…………2分
又∵M为CC1中点 ∴EF∥ C1M
|
而EM ![]() 平面A1B1C1D1 . FC1
平面A1B1C1D1 . FC1![]() 平面A1B1C1D1 .
平面A1B1C1D1 .
∴EM∥平面A1B1C1D1………………6分
(Ⅱ)由(Ⅰ)EM∥平面A1B1C1D1 EM![]() 平面A1BMN
平面A1BMN
平面A1BMN∩平面A1B1C1D1=A1N ∴A1N// EM// FC1
∴N为C1D1 中点
过B1作B1H⊥A1N于H,连BH,根据三垂线定理 BH⊥A1N
∠BHB1即为二面角B—A1N—B1的平面角……8分
设AA1=a, 则AB=2a, ∵A1B1C1D1为正方形
∴A1N=![]() 又∵△A1B1H∽△NA1D1
又∵△A1B1H∽△NA1D1
∴B1H=![]()
在Rt△BB1H中,tan∠BHB1=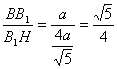 二面角B—A1N—B1的正切值为
二面角B—A1N—B1的正切值为![]() ….12分
….12分
(B)(Ⅰ)建立如图所示空间直角坐标系,设AB=2a,AA1=a(a>0),则
A1(2a,0,a),B(2a, 2a , 0), C(0,2a,0),C1(0,2a,a)……2分
∵E为A1B的中点,M为CC1的中点 ∴E(2a , a , ![]() ),M(0,2a,
),M(0,2a, ![]() )
)
∴EM// A1B1C1D1 …………6分
(Ⅱ)设平面A1BM的法向量为![]() =(x, y , z )
=(x, y , z )
|
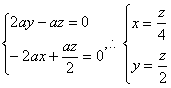
![]() …………9分
…………9分
而平面A1B1C1D1的法向量为![]() .设二面角为
.设二面角为![]() ,则
,则
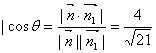 又:二面角为锐二面角
又:二面角为锐二面角 ![]() ,……11分
,……11分
从而![]() ………………12分
………………12分
20.(12分)解:(1)由题意,存款量g(x)=Kx2,银行应支付的利息
h(x)=x·g(x)= Kx3 ……………… (4分)
(2)设银行可获收益为y,则
y=0.048·Kx2–Kx3 ………………(6分)
y’=K·0.096x–3 Kx2 令y’ =0 即K×0.096x–3 Kx2=0
解得x=0 或x=0.032 …………………(9分)
又当x![]() (0,0.032)时,y’>0, x
(0,0.032)时,y’>0, x![]() (0.032,0.048)时, y’<0
(0.032,0.048)时, y’<0
![]() y在(0,0.032)内单调递增,在(0.032,0.048) 单调递减
y在(0,0.032)内单调递增,在(0.032,0.048) 单调递减
故当x=0.032时,y在(0,0.048)内取得极大值,亦即最大值
答:存款利率为3.2%时,银行可获得最大收益 ………………(12分)
21.(I)由已知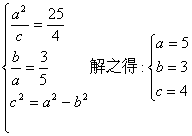 ………………3分
………………3分
∴椭圆的方程为![]() ,双曲线的方程
,双曲线的方程![]() .
.
又![]() ∴双曲线的离心率
∴双曲线的离心率![]() …………………………6分
…………………………6分
(Ⅱ)由(Ⅰ)A(-5,0),B(5,0) 设M![]() 得m为AP的中点
得m为AP的中点
∴P点坐标为![]() 将m、p坐标代入c1、c2方程得
将m、p坐标代入c1、c2方程得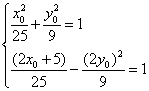
消去y0得![]() 解之得
解之得![]()
由此可得P(10,![]() ………………9分
………………9分
当P为(10,![]() 时 PB:
时 PB:![]() 即
即![]()
代入![]()
![]() MN⊥x轴 即
MN⊥x轴 即![]() …………12分
…………12分
22.解:(1)据题意:f(1)=n2 即a0+a1+a2+a3+……+an= n2
令n=1 则a0+a1=1,a1=1–a0
令n=2 则a0+a1+a2=22,a2=4–(a0+a1)=4–1=3
令n=3 则a0+a1+a2+a3=32,a3=9–(a0+a1+a2)=9–4=5
![]() {an}为等差数列
{an}为等差数列 ![]() d= a3–a2=5–3=2
d= a3–a2=5–3=2
a1=3–2=1 a0=0 an=1+(n–1)·2=2n–1 ………………(6分)
(2)由(1)f(x)= a1x+a2x2+a3x3+……+anxn
n为奇数时,f(–x)=–a1x1+a2x2+a3x3+……+an–1xn–1+anxn ………………(7分)
g(x)=![]() [ f(x)–f(–x)]= a1x1+a3x3+a5x5+……+an–2xn–2+anxn
[ f(x)–f(–x)]= a1x1+a3x3+a5x5+……+an–2xn–2+anxn
g(![]() )=1·(
)=1·(![]() )+5·(
)+5·(![]() )3+……+(2n–5)(
)3+……+(2n–5)(![]() )n--2+(2n-1) (
)n--2+(2n-1) (![]() )n…(8分)
)n…(8分)
![]() g
g![]() =1·
=1·![]() 3+5·
3+5·![]() 5+9·
5+9·![]() 7+……+(2n–5)(
7+……+(2n–5)(![]() )n+(2n-1)
(
)n+(2n-1)
(![]() )n+2
)n+2
相减得![]() g
g![]() =1·
=1·![]() +4[
+4[![]() 3+
3+![]() 5+……+
5+……+![]() n]- (2n-1) (
n]- (2n-1) (![]() )n+2…(9分)
)n+2…(9分)
![]() g
g![]() =
=![]() –
–![]() ·(
·(![]() )n-
)n-![]() (
(![]() )n
…(10分)
)n
…(10分)
令![]() =
=![]() n(
n(![]() )n
)n
![]()
![]() -
-![]() =
=![]() (
(![]() )n·
)n·![]()
![]() 0,n
0,n![]() N*
N*
![]()
![]()
![]()
![]() ,
, ![]() 随n增大而减小
随n增大而减小
又![]() ·
·![]() n随n增大而减小
n随n增大而减小![]() g
g![]() 为n的增函数,当n=1时,g
为n的增函数,当n=1时,g![]() =
=![]()
而![]() –
–![]() ·(
·(![]() )n-
)n-![]() (
(![]() )n<
)n<![]()
![]()
![]()
![]() g
g![]() <
<![]()
![]() 使m< g
使m< g![]() <M恒成立的自然数m的最大值为0,M最小值为2
<M恒成立的自然数m的最大值为0,M最小值为2
M–m的最小值为2注;用其他的方法,求出m的最大值或M最小值之一,可得3分