高三数学第一次调研考试试题及试卷分析(理)
一.试题的整体评价
2004年高三第一次调研考试试题,在充分考查学生“三基”的基础上,加强了对考生综合能力以及分析问题和解决问题能力的考查.试题很多源于课本,不偏不怪。试题类型多样化.保持应用性题目和能力型题目占有较大的比例.试卷的整体难度较2003年高考试题略有降低,(全市平均得分78分,最高分149分,140分以上11人,130分以上64人;2003年高考全市平均分76分,最高分为145分,140分以上1人,130以上11人。)试题体现了2004年高考命题稳中有降的命题方向,考察的基础知识面大量广,突出了对能力的考察,特别注重考察学生的基本能力。同时,注意考察学生综合运用知识的能力。特别降低了最后一题的难度,把一题把关为多题把关。试题表现出稳、新、活的特点。具有较高的区分度和信度.试题对新增数学内容的考查力度较大,对二轮复习有着积极地导向和促进作用.
1体现了《考试说明》的要求
1.1试卷长度、题型比例配置保持与《考试说明》的规定一致.全卷共22题,其中选择题12个,共60分;填空题4个,共16分;解答题6个,共74分.全卷合计150分.
1.2考查的内容面广(见表1),侧重于中学数学学科的重点内容和主要方法,侧重于初等数学和高等数学衔接内容和方法的考查.
表1:考查知识点分布表
| 理科 | ||||
| 题号 | 分值 | |||
| 代数 | 三角 | 2、13、15、16、17 | 30 | |
| 函数 | 1、11 | 10 | ||
| 不等式 | 6、12 | 10 | ||
| 数列 | 7、22 | 19 | ||
| 几何 | 平面向量 | 16、17、20 | 22 | |
| 立体几何 | 4、5、16、19 | 26 | ||
| 解析几何 | 8、10 14、20 | 26 | ||
| 概率统计 | 二项式定理 | 9 | 5 | |
| 排列组合 | 3 | 5 | ||
| 概率 | 18 | 12 | ||
| 导数 | 导数 | 16、21 | 16 | |
| 极限 | 22 | 14 | ||
从试题所涉及到的数学知识和方法以及数学思想来看,试题以中学数学的主体内容为考查的重点,以考试说明教学大纲为依据,对高考中的重点、热点做了重点考察,如有关函数、立体几何、平面向量、导数、数列、概率等内容是联结初等数学和高等数学的纽带,在试题中占较大的比例.
| 理科(280+88课时) | 课时数 | 课时比例 | 分数 | 分数比例 |
| 平面向量 | 12 | 3.3% | 22 | 14.6 |
| 导数 | 18 | 4.9% | 13 | 8.6 |
| 概率统计 | 14 | 3.8% | 12 | 8 |
| 合计 | 44 | 12% | 47 | 31.3 |
2根据高考命题思路,加大新增课程内容在试卷中的比例,新增数学内容由配角转为主角
| 理科 | ||
| 应用题 | 题号 | 3、12、18 |
| 分值 | 22 | |
| 百分比 | 14.6 | |
从表1不难发现,新增数学内容:导数、概率统计、平面向量等在试卷中约47分,占整个卷面分数的近31%,远远高出其在教学大纲中的课时分配所占比例(见表2).同时在设计试题时,给出施展新增数学知识和方法的空间,在一些常见的数学问题中,注意利用知识的交汇点设计题目.如用导数求解函数中的参数范围问题;三角函数与向量结合的题目,向量与求解解析几何中的问题结合等.试题充分体现了对新增知识的重视与运用,与高考命题的思路是一致的。
表2:新增数学内容课时数与在试卷中占分数比例对比
3应用题在试卷中占有一定的比例
通过设置应用题来考查学生应用数学的意识,让学生关心周围的社会和生活的世界,培养正确的世界观和人生观.试题中出现了2小一大3个应用题.理3题是一个用排列组合的知识解决书架放书的问题;理12是一个数学建模问题,如何把一个交通安全问题转化为一个数学问题来解决;理18是用概率的方法来计算爆破中的成功率问题。这些应用题涉及到的问题,切合实际,学生熟悉,容易引起学生的兴趣和关注;同时创设新的试题情景使学生在新的情景中实现知识迁移,创造性地解决问题,更能体现学生的数学素质和能力,它给真正的优秀学生得高分提供了机会,真正考查出学生的学习潜力。对于学生创新意识和实践能力的培养,起到良好的导向作用.
表3:应用题分布表
二.试题分析
1考查“三基”,检验学生的基本数学素质
基础知识、基本方法、基本技能是一切数学能力的基础,离开基础去谈能力那将是无源之水,无本之木.因此对“三基”的考查是试题的重点所在.
例1:理2 已知cosα=1/3,则cos(л+2α)等于
A -![]() B
B![]() C-
C-![]() D
D![]()
解析:此题主要考查诱导和倍角公式,考查学生的基本运算能力.错误原因主要是倍角公式记错,诱导公式符号错.
例2:理3 书架上的一格内有排好顺序的6本书,如果保持这6本书的相对顺序不变,再放上2本书,则不同的放法有
A 20种 B 30种 C 42种 D 56种
解析:此题主要考察了两个基本原理的运用,. 错误原因主要是漏了两本书相邻的情况..
例3:理4 给出下面两个命题:甲命题:若平面α⊥平面 β ,平面β⊥ 平面γ ,则平面α ∥ 平面γ ;乙命题:若平面α 上不共线的三点到平面β 的距离相等,则α ∥β ,下列说法正确的是
A 甲乙都真 B 甲真乙假 C 甲假乙真 D 甲乙都假
解析:此题主要考查两个平面的位置关系,命题真要证明,假举反例.
例4 理5 已知点P 、A、 B、 C 在同一球面上,PA 、PB 、PC 两两垂直, PA=1,PB=2,PC=3, 则该球的表面积是
A ![]() л B 14л C 56л
D 196л
л B 14л C 56л
D 196л
解析:记住基本结论PA![]() + PB
+ PB![]() + PC
+ PC![]() = 4R
= 4R![]() 即可。或看成长方体的三棱。
即可。或看成长方体的三棱。
例5 理6
已知A=〔x∣x![]() -5x-6>0〕,B=〔x∣∣x-5∣<a〕,a为常数且 11 ∈B,则
-5x-6>0〕,B=〔x∣∣x-5∣<a〕,a为常数且 11 ∈B,则
A A∪ B=R B (
C![]() B)∪A=R C (
C
B)∪A=R C (
C![]() A)∪(C
A)∪(C![]() B)=R D (C
B)=R D (C![]() A)∪B=R
A)∪B=R
本题考察了集合的一些概念和运算法则,基本不等式的解法。;
解析:由11 ∈B,得a>6,得出结论。
例6 理13
ΔABC中,![]() 则ΔABC的面积为(
则ΔABC的面积为(![]() )
)
本题考察了正弦定理的运用以及解三角形。
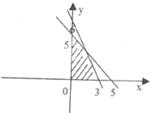 理14.右图中阴影部分的点满足不等式组
理14.右图中阴影部分的点满足不等式组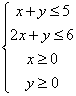 ,这些点中使目标函数z=6x+8y,取得最大值的点坐标是 (0,5).
,这些点中使目标函数z=6x+8y,取得最大值的点坐标是 (0,5).
理16.给出下列命题:
①f(x0)是函数f(x)的极值,则必有f’(x0)=0;
②过空间一点,平面的法向量是唯一的;
③f(x)=sinx+cosx (![]() )的图像关于(
)的图像关于(![]() ,0)(
,0)(![]() )点对称;
)点对称;
④将圆![]() 按a=(2,1)平移后与x+y+m=0相切,则实数m的值是-1或-5.
按a=(2,1)平移后与x+y+m=0相切,则实数m的值是-1或-5.
其中正确的命题是③④.(写出所有正确的命题代号)
例7 理17 .已知A(-1,0),B(0,1)C(sinα, cosα),
(I)若![]() ,求sin2α的值.
,求sin2α的值.
(II)若![]() ,α∈(0,π),求
,α∈(0,π),求![]() 的夹角.
的夹角.
本题主要考察了平面向量的基本运算以及三角函数公式的一些运用。在三角函数和平面向量的知识交汇点设计题目这也是高考命题的方向。

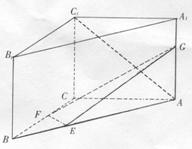
例8 理19 .如图,已知直三棱柱ABC-A1B1C1中,AC=BC=AA1,AC⊥BC,F为BC之中点,E在AB上,且BA=3BE,G为AA1上一动点.
(I)若AC1⊥EG,试确定G点的位置;
(II)在满足条件(I)的情况下,试求异面直线AC1与FG所成的角;
(III)在满足条件(I)的情况下,求点A到平面EFG的距离.
本题主要考察了空间中点、线、面的一些基本问题以及解决这些问题基本方法。



2 注重数学能力考察,知识只是能力的载体.
例9:理7 等差数列{a![]() } 中,S
} 中,S![]() =-36,S
=-36,S![]() =-104,等比数列{b
=-104,等比数列{b![]() }中,b
}中,b![]() = a
= a![]() ,b
,b![]() = a
= a![]() ,则b
,则b![]() =
=
A 4![]() B - 4
B - 4![]() C
C ![]() 4
4![]() D 无法确定
D 无法确定
解析 本题主要考查等差、等比数列的一些性质运用及其数学思维和运算能力。
由b![]() = b
= b![]() b
b![]() = a
= a![]() a
a![]() ,又S
,又S![]() =
=![]() (a
(a![]() +a
+a![]() )9=9 a
)9=9 a![]() ,所以 a
,所以 a![]() =-4,同理 a
=-4,同理 a![]() =-8
=-8
所以b![]() =
=![]() 4
4![]()
例10:理9 如果(![]() +2x)
+2x)![]() =a
=a![]() +a
+a![]() x+a
x+a![]() x+…+a
x+…+a![]() x
x
那么(a![]() + a
+ a![]() + …+a
+ …+a![]() )
)![]() -( a
-( a![]() + a
+ a![]() +…+a
+…+a![]() )
)![]() =
=
A 1 B -1 C 2 D -2
解析 本题考察了二项式系数的一些性质,考察了学生的转化和运算能力。
f(x)= (![]() +2x)
+2x)![]() ,f(1)= a
,f(1)= a![]() +a
+a![]() +a
+a![]() +…+a
+…+a![]() , f(-1)= a
, f(-1)= a![]() -a
-a![]() +a
+a![]() -…-a
-…-a![]() ,
,
所以所求为-f(1) f(-1)=1.
例11:理12 已知一个驾驶员喝了少量酒后,血液中酒精含量迅速上升到0.3mg/ml,在停止喝酒后,酒精含量就以每小时25%的速度减少,为了保障交通安全,某地规定驾驶员学液中的酒精含量不超过0.09mg/ml,则该驾驶员喝少量酒后到能驾驶时至少经过的小时数是(lg2=0.3010,lg3=0.4771)
A 6.2 B 5.2 C 4.2 D 3.2
解析 本题注要考查学生的数学建模能力,如何对客观事物中的数量关系和数量关系和数学模式作出思考和判断。
转化为不等式 0.3× 0.75![]() ≤ 0.09 , n≥ 4.2
≤ 0.09 , n≥ 4.2
例12 理18 .要进行某种爆破试验,设爆破成功的概率为![]() ,而现有材料只能提供10个试验.
,而现有材料只能提供10个试验.
(I)恰好第二个爆破成功的概率室多少?
(II)要是爆破以99.6%的把握成功,问现有材料是否满足?若能满足,至少需要同时进行几个爆破试验?(lg2=0.3010)
本题考查了如何利用概率的知识解决实际问题,考查了学生的实际应用能力。
解:设第I个爆破试验成功记为![]() ,因为每个爆破试验都是独立的,
,因为每个爆破试验都是独立的,
![]()
所以恰好第二个爆破试验成功的概率为![]() .
.
现有材料能够满足,至少同时进行6个爆破试验.
设至少同时进行能n个爆破试验,则这n个爆破试验不成功时的概率为![]() ,
,
![]()
两边取以10为底的对数,得, 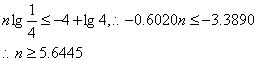
故至少需要同事进行6个爆破试验.
例13 理22 .已知点列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(I)求过点P0,P1的直线l的方程;
(II)判断![]() 与l的关系,并证明你的结论;
与l的关系,并证明你的结论;
(III)当![]() 时,求
时,求![]() 的极限.
的极限.
本题考查了直线斜率,直线方程,点与直线的位置关系;数列、数学归纳法的一些知识,试题情景新颖,学生要在新的情景中实现知识迁移,必须有较强的直觉猜想能力、数学探究能力、和数学思维能力。
解: (I)
![]()
![]() ,
,![]() ,
,![]() .
.![]() .
.
(II) ![]() ,
,![]() 验证得这两点在l上,猜想:
验证得这两点在l上,猜想: ![]() 也在直线l上.
也在直线l上.
用数学归纳法证明:
①当n=2是,成立.
②假设n=k(![]() )时成立,即
)时成立,即![]()
那么当n=k+1时, 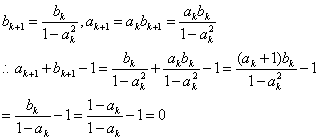
即![]()
所以当n=k+1时也成立
综上, ![]() 在直线l上.
在直线l上.
(III) 
3考查数学思想方法,反映数学内在规律和特点
3.1分类讨论的思想,这是数学试卷(特别是理科)必考内容之一.
例14:理21.已知函数![]()
(I)要使f(x)在(0,1)上单调递增,试求a的取值范围;
( II)若![]() 时,设y=f(x)上任意一点处的切线的斜率为k,当
时,设y=f(x)上任意一点处的切线的斜率为k,当![]() 时,求a的范围.
时,求a的范围.
本题主要考查应用导数研究函数的方法及推理和运算能力,考查了分类讨论的数学思想.
解: (!)![]() ,要使f(x)在(0,1)上单调递增,则
,要使f(x)在(0,1)上单调递增,则![]() 在
在![]() 时恒成立.
时恒成立. ![]() 在
在![]() 时恒成立,
时恒成立, ![]() ,即a的取值范围是
,即a的取值范围是![]() .
.
(2)
当![]() 时,
时, ![]() ,即对于任意
,即对于任意![]() ,
,![]() .
.
①,当![]() ,即
,即![]() 时,只要
时,只要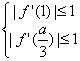 ,即
,即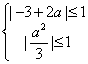 ,解得
,解得![]()
②当![]() 时,即
时,即![]() 时,只要
时,只要![]() ,即
,即![]() ,解得
,解得![]() ,此时
,此时![]()
③当![]() 时,即
时,即![]() ,只要
,只要![]() ,即
,即![]() ,解得
,解得![]() ,此时
,此时![]() .
.
综上,a的取值范围是![]() .2
.2
.
 3.2数形结合的思想
3.2数形结合的思想
例 15理1 已知A={y y=log![]() x,x>1},B={y y=(
x,x>1},B={y y=(![]() )
)![]() ,x>1},A∩ B=
,x>1},A∩ B=
A (![]() ,+∞)
B (
,+∞)
B (![]() ,2)
C (0,
,2)
C (0,![]() )
D(0,2)
)
D(0,2)
此题主要考查函数的基本性质以及数形结合的数学思想.
解析:利用图象马上得出结论。
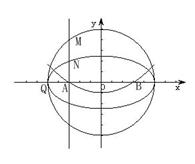 例16:理8 已知⊙O:x
例16:理8 已知⊙O:x![]() + y
+ y![]() =25,点 A(-3,0),B(3,0,),一列抛物线以 ⊙O 的切线为准线且过A 、B 两点,则这列抛物线的焦点轨迹是
=25,点 A(-3,0),B(3,0,),一列抛物线以 ⊙O 的切线为准线且过A 、B 两点,则这列抛物线的焦点轨迹是
A ![]() +
+![]() =1(x≠0) B
=1(x≠0) B ![]() +
+![]() =1(y≠0)
C
=1(y≠0)
C ![]() +
+![]() =1(x≠0)
D
=1(x≠0)
D![]() +
+![]() =1 (y≠0)
=1 (y≠0)
此题主要是在运动变换过程中考查数学思维能力和数形结合的数学思想,考查抛物线、椭圆的性质及其运用.
解析:答案已经定性为椭圆.
采用特殊值法:F(0,4)满足条件,排除C D, 若 Q(-5,0)为焦点,由图知
AQ<AN<AM,所以Q(-5,0)为焦点不成立。
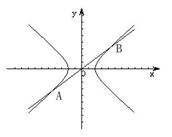 .例17 理10 过双曲线
.例17 理10 过双曲线![]() -
-![]() =1的中心作直线 l ,交双曲线与 A、B
两点,
P是双曲线上不同于A、 B 的一点,且 PA、 PB 都不与 y 轴平行,则直线PA 和PB 的斜率之积
=1的中心作直线 l ,交双曲线与 A、B
两点,
P是双曲线上不同于A、 B 的一点,且 PA、 PB 都不与 y 轴平行,则直线PA 和PB 的斜率之积
A 等于常数-![]() B 等于常数
B 等于常数 ![]() C
等于常数-
C
等于常数-![]() 或
或 ![]() D 一定为负值
D 一定为负值
解析:此题主要是在运动变换过程中考查数学思维能力和数形结合的数学思想,考查双曲线的性质及其运用
解析;设直线为 y=x, 当 P 在双曲线上时,由图知,直线PA 和PB 的斜率之积始终为正。或设A(m,n),则B(-m,-n),P(a,b),利用点在曲线上计算斜率之积。
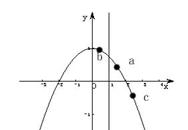
例18理11 偶函数f(x) 的定义域为(-∞,+∞) ,且在(-∞,0) 上是增函数,a=f(ln![]() ),b=f(log
),b=f(log![]() 3),c=f(0.4
3),c=f(0.4![]() ),
),
则 a、 b 、c 的大小关系是
A c<a<b B a<c<b C b<a<c D c<b<a
本题考察了函数的单调性,偶函数的性质以及数型结合的基本思想。
解析:f(ln![]() )=f(ln4),1<ln4<2, 0<log
)=f(ln4),1<ln4<2, 0<log![]() 3<1, 0.4
3<1, 0.4![]() >2.5,由图像得出。
>2.5,由图像得出。
3.3转化与化归的思想
例19:理15. 已知![]() ,则f(1)+f(2)+f(3)+…+f(2003)=0.
,则f(1)+f(2)+f(3)+…+f(2003)=0.
解析:此题主要考查转化的思想,将函数值的和向数列转化、迁移,考查学生分析、归纳、、转化、化归的数学能力.
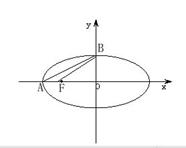 例20 理20在△ABF中,
例20 理20在△ABF中, ![]() , △ABF的面积
, △ABF的面积![]() ,设椭圆以F为焦点,A、B为顶点.
,设椭圆以F为焦点,A、B为顶点.
(I)求椭圆的方程;
(II)若椭圆上有一动点P使△PAB的面积最大,试求P点坐标.
.
向量的知识和方法与解析几何中的一些基本问题的结合,是近几年本部分高考命题的一个热点。此题主要考查平面向量、三角形面积、椭圆的基础知识,求曲线方程的方法、面积最值问题的转化,考查学生分析、转化、化归的数学能力.
解:

