高三基础测试数学试卷
一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中有一项是最符合题目要求的）
1．有以下关于满足A⊆B的非空集合A，B的四个命题：
①若任取x∈A，则x∈B是必然事件；②若x
A，则x∈B是不可能事件；
③若任取x∈B，则x∈A是随机事件；④若xB，则xA是必然事件。
上述命题中正确的个数是 （ ）
A、1 B、2 C、3 D、4
2．若
e，
e，且
，则四边形ABCD是
( )
A.平行四边形 B.菱形 C.等腰梯形 D.非等腰梯形
3．
≤2的必要不充分条件是 ( )
A．
≤3 B．≤2 C．≤1 D．
≤ 1
4．二次函数
则实数a的取值范围是 ( ) A．a≥0 B．a≤0 C．0≤a≤4 D．a≤0或a≥4
5. 圆C切y轴于点M且过抛物线
与x轴的两个交点，O为原点，则OM的长是( )
A．4 B．
C．
D．2
6．二面角
的平面角为
，直线
⊥
，则与
所成的角为 （ ）
A．
B．
C．
D．或
7．已知一个简单多面体的每个顶点处都有三条棱，则顶点数V与面数F满足的关系式是 ( )
A．2F+V=4； B．2F－V=4； C．2F+V=2； D．2F－V=2；
8.在5张卡片上分别写着数字1、2、3、4、5，然后把它们混合，再任意排成一行，则得到的数能被5或2整除的概率是 ( )
A. 0.8 B. 0.6 C. 0.4 D. 0.2
9. 设θ是三角形的一个内角，且sinθ＋cosθ＝
，则方程x2sinθ－y2cosθ＝1表示( )
A.焦点在x轴上的椭圆 B.焦点在y轴上的椭圆
C.焦点在x轴上的双曲线 D.焦点在y轴上的双曲线
10．对于二项式
，四位同学作出了四种判断：①存在n∈N+，展开式中有常数项； ②对任意n∈N+，展开式中没有常数项； ③对任意n∈N+，展开式中没有x的五次项；④存在n∈N+，展开式中有x的五次项.上述判断中正确的是 （ ）
A．①与③ B．②与③ C．②与④ D．④与①
11.数列{an}满足a1=0，an+1= an+2n，那么a2004的值是 ( )
A.2002×2003 B.2003×2004 C.2004×2005 D.20042
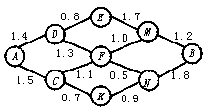
12.如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相连，连线上标注的数字表示某信息经过该段网线所需的时间(单位：毫秒).信息由结点A传递到结点B所需的最短时间为 ( )
A.5毫秒 B.4.9毫秒 C.4.8毫秒 D.4.7毫秒
二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）
13．在△ABC中，
cos(B+C)+cos(
+A)的取值范围是
.
14. 二次曲线
，当
时，该曲线的离心率
的取值范围是
15.设2x+y≥1，则函数u=(x+2)2+(y–1)2的最小值是 。
16.给出下列命题：
(1){正四棱柱}∩{长方体}={正方体}；(2)不等式x2-4ax+3a2＜0的解集为{x│a＜x＜3a}；
(3)若不等式x－4＋x－3＜a的解集为空集，必有a≥1 (4)函数y=f(x)的图像与直线x=a至多有一个交点；(5)若角，β满足cos·cos
＝1，则sin（＋）＝0.
其中正确命题的序号是 .
数学答卷
| 得 分 | 评卷人 |
|
|
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
| 得 分 | 评卷人 |
|
|
二、填空题
13. 。 14. 。
15. 。 16. 。
三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）
| 得 分 | 评卷人 |
|
|
|
17.(本题满分12分) 已知函数f(x)=Asinωx+Bcosωx(其中A、B，ω是实常数，ω>0)的最小正周期为2，并且当
时，f(x)取得最大值2。
(1)求函数f(x)的解析式；
(2)函数y=f(x)(x∈R)的图象是否在闭区间[
]上存在对称轴？如果存在，求出其对称轴的方程；如果不存在，请说明理由。
| 得 分 | 评卷人 |
|
|
18. 设抛物线C1：
与抛物线C2：
在它们一个交点处的切线互相垂直。(1)求a、b之间的关系；(2)若a＞0，b＞0，求ab最大值。
| 得 分 | 评卷人 |
|
|
19.（本题满分12分）梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=，SD=
，在线段SA上取一点E（不含端点）使EC=AC，截面CDE与SB交于点F。
（1）求证：四边形EFCD为直角梯形；
（2）求二面角B-EF-C的平面角的正切值；
（3）设SB的中点为M，当
的值是多少时，能使△DMC为直角三角形？
请给出证明.
| 得 分 | 评卷人 |
|
|
20．(本题满分12分) 已知
=(x,0)，
=(1，y)，(
+
)
(–)⑴求点
(x，y)的轨迹C的方程；⑵若直线l：y=kx+m(k≠0)与曲线C交于A、B两点，D(0，–1)，且有
(
-
)⊥(+)，试求m的取值范围。
21．（本小题满分12分）某集团从2001年起投资兴办甲、乙两个企业，预期目标为两企业
| 得 分 | 评卷人 |
|
|
年利润之和是1160万元。其中乙企业的产品受某些因素的影响，利润逐年呈等比数列递减，所以不再追加投资金额，而甲企业的利润保持不变，所以每年都增加投资金额，并使每年的投资金额呈等比数列递增。具体数据请看下表。
| 甲企业 | 乙企业 | 两企业利润之和与预期目标的差额 | |||||
| 投资金额 | 利润率 | 利润 | 投资金额 | 利润率 | 利润 | ||
| 2001年 | 1000 | 25.6% | 256 | 1000 | 62.5% | 625 | -279 |
| 2002年 | 1250 | 25.6% | 320 | 1000 | 50% | 500 | -340 |
| 2003年 | 1562.5 | 25.6% | 400 | ||||
（1）请完成表格中空白部分；
（2）试确定哪一年两企业利润之和最小；
（3）试确定哪一年起两企业利润之和超过预期目标。
| 得 分 | 评卷人 |
|
|
22．（本题满分14分）函数f(x)=loga(x－3a)(a＞0,且a≠1),当点P（x,y)是函数y=f(x)图象上的点时，Q(x－2a,－y)是函数y=g(x)图象上的点。
（Ⅰ）写出函数y=g(x)的解析式。
（Ⅱ）当x∈［a+2,a+3］时，恒有f(x)－g(x)≤1,试确定a的取值范围。
高三基础测试数学试卷答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | A | D | D | C | B | B | B | D | B | C |
二、填空题：
13. [-2，
) 14. [
，
) 15.
16.(4)、(5)
三、解答题：
17解：(1)∵T=2 ∴
……………2’
∵时f(x) 取得最大值2 ∴Asin
+Bcos=
=2……………6’
∴A=,B=1；∴
…………………8’
(2)∵f(x)的对称轴为
＝
(k∈Z) 即x=k+
∴当且仅当k=3时x=k+∈[]∴在闭区间上有且只有一条对称轴
………………12’
18解：(1)设C1与C2的一个交点是P(x0，y0)，则x02-2x0+2= -x02+ax0+b
∴2x02-(2+a)x0+2-b=0……………①……………3’
∵C1、C2在交点P(x0，y0)处的切线互相垂直∴(2x0-2)(-2x0+a)=-1
∴-4x02+2(2+a)x0+1-2a=0……………②……………6’
∴①×2+②得2a+2b=5 ∴a+b=
………………8’
(2)ab≤
=
∴当a=b=
时,ab取最大值…………12’
19.证明：
（1）∵ CD∥AB，AB
平面SAB ∴CD∥平面SAB,
平面EFCD∩面SAB=EF，
∴CD∥EF ∵
又
面
∴
平面SAD，∴
又
为直角梯形 …………………………4’
（2）
平面
∥
平面SAD
即为二面角D—EF—C的平面角
中
而
且
为等腰三角形，
………………8’
(3)当
时，
为直角三角形 .
,
平面
平面
.
在
中，
为SB中点，
.
平面
平面 
为直角三角形 …………12’
20．解：(1)∵ (+)(–)∴(+).(–)=0 …………2’
∴2–32=0 ∴x2-3y2=3 ∴点(x，y)的轨迹C的方程是x2-3y2=3…………4’
(2)设点A(x1，y1)，B(x2，y2)则
∴（1-3k2）x2-6kmx-3m2-3=0
…………5’∴
∴3k2<m2+1 ①………………7’
又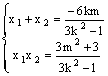
∵(-)⊥(+)∴(-).(+)=0
∴=∴x12+(y1+1)2=x22+(y2+1)2又点A、B在l上∴x1+x2+k[k(x1+x2)+2m+2]=0
∴-6km+k[k(-6km)+2(m+1)(3k2-1)] ∵k≠0 ∴4m+1=3k2 ②……9’
∵1-3k2≠0 ∴m≠0 ∴3k2=4m+1>0 m>
…………10’
由①②得m2-4m>0∴m<0或m>4………………11’∴m的取值范围是<m<0或m>4 ……12’
21． 解：(1)1000 40% 400 -360 …………………4’
(2)设甲企业第n年利润为an，乙企业第n年利润为bn(2001年为第1年) 
∴得润之和为
(万元) 当且仅当
∴2003年两企业利润之和最小。………8’ (3) 
则 x2·256-1160x+625≥0 ∴
或
…9’
∴
∴
∴ 
∴
∴2008年两企业利润之和超过预期目标。……………………12’
22．解：（Ⅰ）设P(x0,y0)是y=f(x)图象上点，Q（x,y）,则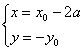
，
∴
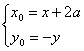∴－y=loga(x+2a－3a)，∴y=loga
(x＞a) ……… 5分
（Ⅱ）
∴x＞3a ∵f(x)与g(x)在［a+2,a+3］上有意义. ∴3a＜a+2
∴0＜a＜1 ……………………7分
∵f(x)－g(x)≤1恒成立
loga(x－3a)(x－a)≤1恒成立.
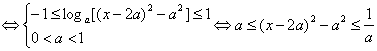…………9分
对x∈［a+2,a+3］上恒成立，令h(x)=(x－2a)2－a2
其对称轴x=2a,2a＜2,2＜a+2
∴当x∈［a+2,a+3］
hmin(x)=h(a+2)，hmax=h(a+3)
∴原问题等价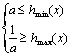
…………………… 12分
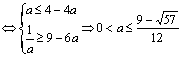……………………14分