高三级11月份月考数学试卷
（启用前绝密）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页。第Ⅱ卷3至5页。满分150分。考试时间120分钟。
第Ⅰ卷（选择题 共60分）
参考公式：
1．如果事件A、B互斥，那么P(A+B)=P(A)+P(B)
2．如果事件A、B相互独立，那么P(A·B)=P(A)·P(B)
3．如果事件A在一次试验中发生的概率为P，那么n次独立重复试验中恰好发生k次的概率为
。
4.球的表面积公式S=4
,其中R表示球的半径.
5.球的体积公式
,其中R表示球的半径.
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）在[0，2
]上满足sinx
1/2的x的取值范围是 （ ）
A． [0，
] B．[
]
C．[
] D．[
]
（2）一个三棱锥各侧面与底面所成的二面角为
，底面三角形三边之长分别为3，4，5，则此三棱锥的侧面积为 （ ）
A．6 B．10 C．12 D．24
（3）已知等比数列
中，
，
和
是方程
的两个根，则
的值是 （ ）
A．16 B．128 C．64 D．32
（4）双曲线
上的点到一个焦点的距离为12，则到另一个焦点的距离为 （ ）
A． 7 B．18或6 C．20或4 D．22或2
（5）设
、
是两个非零向量，则
是
的 （ ）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．非充分非必要条件
（6）动点在圆
上移动时，它与定点B（3，0）连线的中点轨迹方程是
（ ）
A．
B．
C．
D．
（7）函数
的最小值与最大值分别是 （ ）
（A）－4，4 （B）－4，
（C），4 （D）
，
（8）在球面上有四个点A、B、C、D，若AB、AC、AD两两垂直，且AB=3，AC=4，AD=5，那么球面的表面积是 （ ）
A．
B．
C．
D． 
（9）已知集合
，集合
，f是从集合A到集合B的映射，且B中的元素在A中都有原象，则这样的映射共有 （ ）
A．36个
B．24个 C．72个
D．
个
（10）函数
的最大值是
，那么实数a的取值范围是 （ ）
A．
B．
C．
D．
（11）已知数列的前n项和
，则此数列的奇数项的前n项和为 （ ）
A．
B．
C．
D．
（12）若
的两根，则
（ ）
A．
B．
C．lg
D．
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题；每小题4分，共16分。
（13）若复数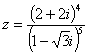
（i为虚数单位），则
__________.
（14）一个袋子里装有大小相同的3个白球和2个红球，从中同时取出2个，则其中含有红球的数学期望为__________.
（15）设有四个命题①底面是矩形的平行六面体是长方体；②棱长相等的直四棱柱是正方体；③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体；④对角线相等的平行六面体是直平行六面体。以上四个命题中，为真命题的是__________（填命题的序号）
（16）等差数列中，其前n项和为
，且
，
，则
_____.
答 卷
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
13___________ 14_____________
15___________ 16_____________
三、解答题：本大题共6小题，共74分；要求写出必要的文字说明和演算步骤。
（17）（本小题满分12分）
甲乙两人各进行一次射击，如果两人击中目标的概率都是0.6，计算：
（1）两人都击中目标的概率;
（2）其中恰有一人击中目标的概率;
（3）至少有一人击中目标的概率
（18）（本小题满分12分）已知顶点在原点，焦点在x轴上的抛物线被直线y=2x+1截得的弦长为
，求抛物线的方程.
（19）（本小题满分12分）
已知
，
，其中
， （1）求证：
与
互相垂直; （2）若k≠0，且向量
与
的大小相等，求
的值
（20）（本小题满分12分）
直三棱柱
，底面
中，CA=CB=1，
，棱
，M、N分别为
，
的中点.
（1）求
的长；（2）求证：
；（3）求
的值
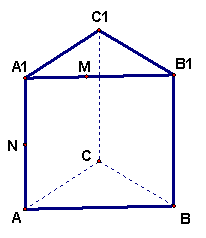
（21）（本小题满分12分）
某地有一水库，设计最大容量是128000
，经测算在大雨季节注入水库的水量（单位）与天数n
的关系是
，设水库原有水量80000，泄水闸每天泄水量为4000，若在连续大雨的第一天就开闸泄水，问10天中堤坝是否会发生危险？若会，请你计算在第几天发生危险？若不会，请说明理由。
（22）（本小题满分14分） 定义在
上的函数
满足：①对任意
、
,都有
；②当
时，有
.
证明：（I）函数在上的图象关于原点对称；
（II）函数在
上是单调减函数；
（III）
.